On the Number of Samples Needed to Learn the Correct Structure of a Bayesian Network

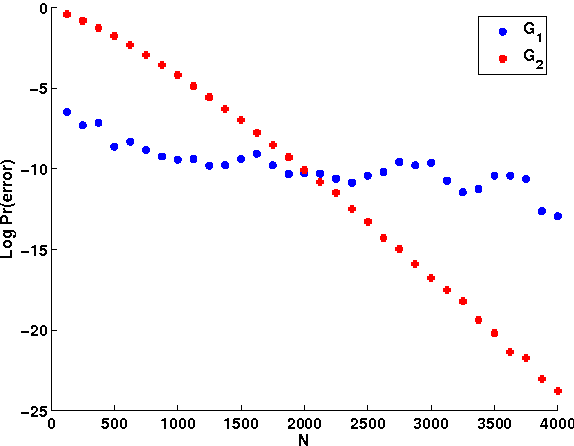
Bayesian Networks (BNs) are useful tools giving a natural and compact representation of joint probability distributions. In many applications one needs to learn a Bayesian Network (BN) from data. In this context, it is important to understand the number of samples needed in order to guarantee a successful learning. Previous work have studied BNs sample complexity, yet it mainly focused on the requirement that the learned distribution will be close to the original distribution which generated the data. In this work, we study a different aspect of the learning, namely the number of samples needed in order to learn the correct structure of the network. We give both asymptotic results, valid in the large sample limit, and experimental results, demonstrating the learning behavior for feasible sample sizes. We show that structure learning is a more difficult task, compared to approximating the correct distribution, in the sense that it requires a much larger number of samples, regardless of the computational power available for the learner.

Ranking Under Uncertainty

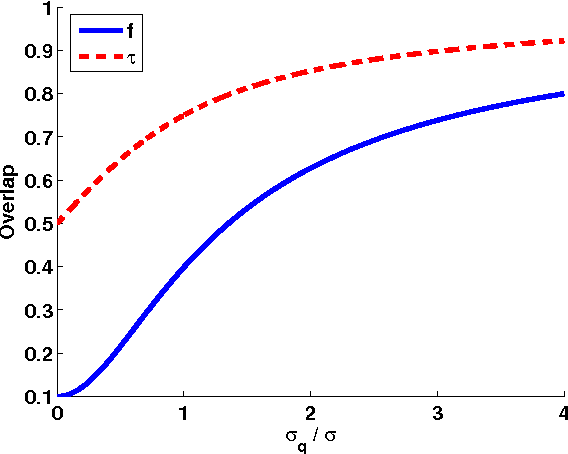
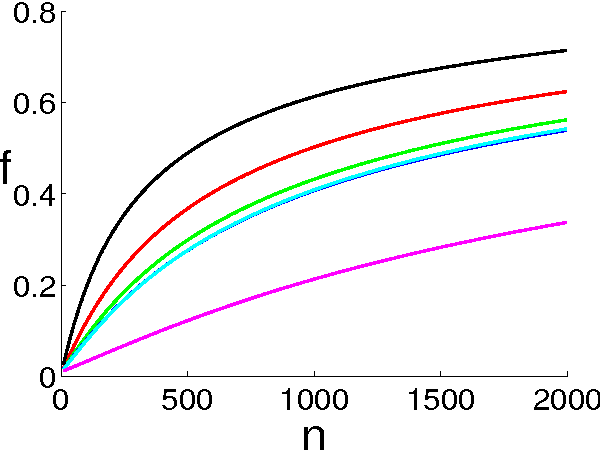
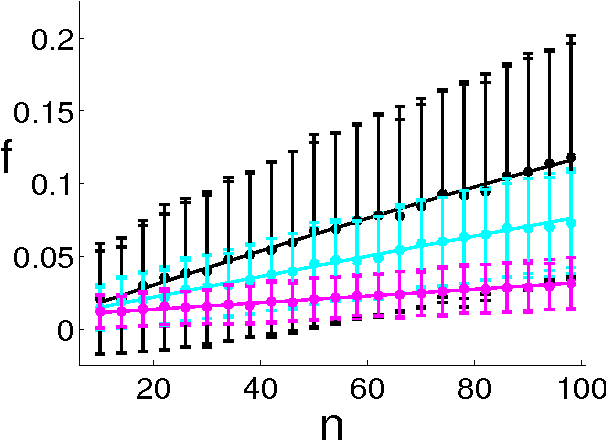
Ranking objects is a simple and natural procedure for organizing data. It is often performed by assigning a quality score to each object according to its relevance to the problem at hand. Ranking is widely used for object selection, when resources are limited and it is necessary to select a subset of most relevant objects for further processing. In real world situations, the object's scores are often calculated from noisy measurements, casting doubt on the ranking reliability. We introduce an analytical method for assessing the influence of noise levels on the ranking reliability. We use two similarity measures for reliability evaluation, Top-K-List overlap and Kendall's tau measure, and show that the former is much more sensitive to noise than the latter. We apply our method to gene selection in a series of microarray experiments of several cancer types. The results indicate that the reliability of the lists obtained from these experiments is very poor, and that experiment sizes which are necessary for attaining reasonably stable Top-K-Lists are much larger than those currently available. Simulations support our analytical results.

Semi-Supervised Learning -- A Statistical Physics Approach

We present a novel approach to semi-supervised learning which is based on statistical physics. Most of the former work in the field of semi-supervised learning classifies the points by minimizing a certain energy function, which corresponds to a minimal k-way cut solution. In contrast to these methods, we estimate the distribution of classifications, instead of the sole minimal k-way cut, which yields more accurate and robust results. Our approach may be applied to all energy functions used for semi-supervised learning. The method is based on sampling using a Multicanonical Markov chain Monte-Carlo algorithm, and has a straightforward probabilistic interpretation, which allows for soft assignments of points to classes, and also to cope with yet unseen class types. The suggested approach is demonstrated on a toy data set and on two real-life data sets of gene expression.