Conservative Exploration in Reinforcement Learning

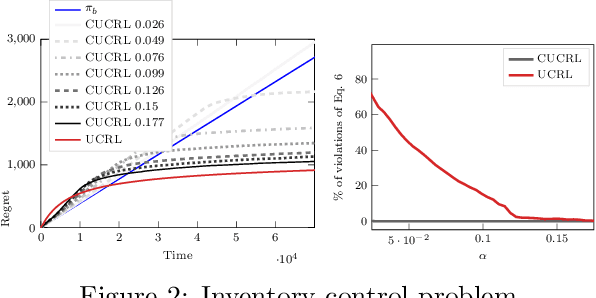
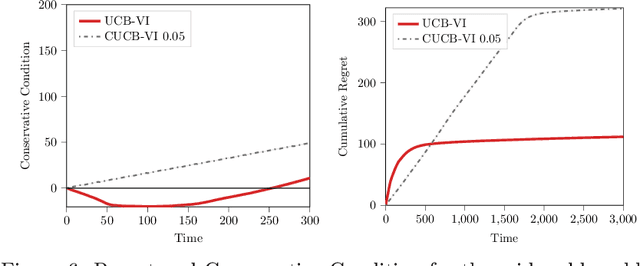
While learning in an unknown Markov Decision Process (MDP), an agent should trade off exploration to discover new information about the MDP, and exploitation of the current knowledge to maximize the reward. Although the agent will eventually learn a good or optimal policy, there is no guarantee on the quality of the intermediate policies. This lack of control is undesired in real-world applications where a minimum requirement is that the executed policies are guaranteed to perform at least as well as an existing baseline. In this paper, we introduce the notion of conservative exploration for average reward and finite horizon problems. We present two optimistic algorithms that guarantee (w.h.p.) that the conservative constraint is never violated during learning. We derive regret bounds showing that being conservative does not hinder the learning ability of these algorithms.

No-Regret Exploration in Goal-Oriented Reinforcement Learning

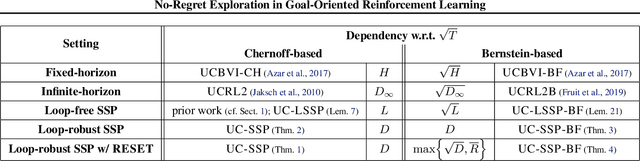
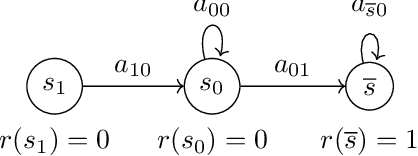
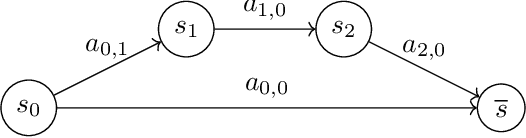
Many popular reinforcement learning problems (e.g., navigation in a maze, some Atari games, mountain car) are instances of the episodic setting under its stochastic shortest path (SSP) formulation, where an agent has to achieve a goal state while minimizing the cumulative cost. Despite the popularity of this setting, the exploration-exploitation dilemma has been sparsely studied in general SSP problems, with most of the theoretical literature focusing on different problems (i.e., fixed-horizon and infinite-horizon) or making the restrictive loop-free SSP assumption (i.e., no state can be visited twice during an episode). In this paper, we study the general SSP problem with no assumption on its dynamics (some policies may actually never reach the goal). We introduce UC-SSP, the first no-regret algorithm in this setting, and prove a regret bound scaling as $\displaystyle \widetilde{\mathcal{O}}( D S \sqrt{ A D K})$ after $K$ episodes for any unknown SSP with $S$ states, $A$ actions, positive costs and SSP-diameter $D$, defined as the smallest expected hitting time from any starting state to the goal. We achieve this result by crafting a novel stopping rule, such that UC-SSP may interrupt the current policy if it is taking too long to achieve the goal and switch to alternative policies that are designed to rapidly terminate the episode.

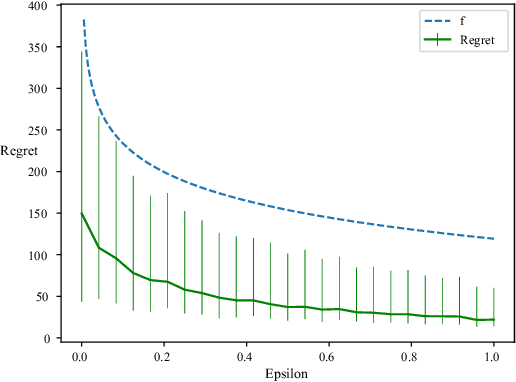
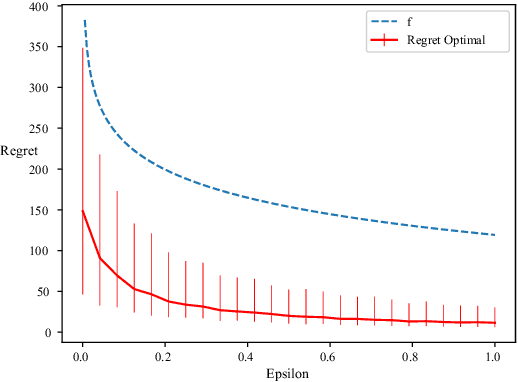
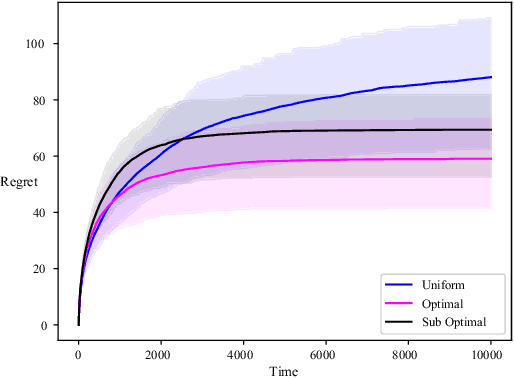
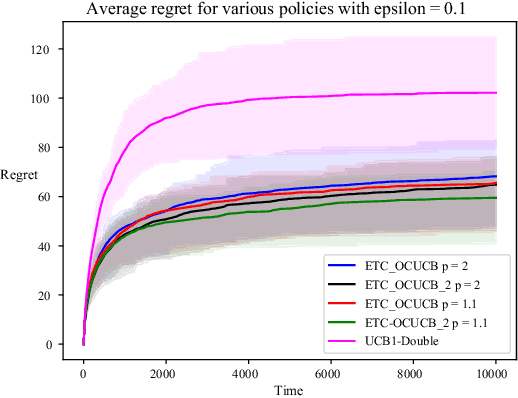
Bandits with Side Observations: Bounded vs. Logarithmic Regret

We consider the classical stochastic multi-armed bandit but where, from time to time and roughly with frequency $\epsilon$, an extra observation is gathered by the agent for free. We prove that, no matter how small $\epsilon$ is the agent can ensure a regret uniformly bounded in time. More precisely, we construct an algorithm with a regret smaller than $\sum_i \frac{\log(1/\epsilon)}{\Delta_i}$, up to multiplicative constant and loglog terms. We also prove a matching lower-bound, stating that no reasonable algorithm can outperform this quantity.