A Unified Theory of Quantum Neural Network Loss Landscapes

Classical neural networks with random initialization famously behave as Gaussian processes in the limit of many neurons, with the architecture of the network determining the covariance of the associated process. This limit allows one to completely characterize the training behavior of such networks and show that, generally, classical neural networks train efficiently via gradient descent. No such general understanding exists for quantum neural networks (QNNs), which -- outside of certain special cases -- are known to not behave as Gaussian processes when randomly initialized. We here prove that instead QNNs and their first two derivatives generally form what we call Wishart processes, where now certain algebraic properties of the network determine the hyperparameters of the process. This Wishart process description allows us to, for the first time: 1. Give necessary and sufficient conditions for a QNN architecture to have a Gaussian process limit. 2. Calculate the full gradient distribution, unifying previously known barren plateau results. 3. Calculate the local minima distribution of algebraically constrained QNNs. The transition from trainability to untrainability in each of these contexts is governed by a single parameter we call the "degrees of freedom" of the network architecture. We thus end by proposing a formal definition for the "trainability" of a given QNN architecture using this experimentally accessible quantity.

Arbitrary Polynomial Separations in Trainable Quantum Machine Learning

Recent theoretical results in quantum machine learning have demonstrated a general trade-off between the expressive power of quantum neural networks (QNNs) and their trainability; as a corollary of these results, practical exponential separations in expressive power over classical machine learning models are believed to be infeasible as such QNNs take a time to train that is exponential in the model size. We here circumvent these negative results by constructing a hierarchy of efficiently trainable QNNs that exhibit unconditionally provable, polynomial memory separations of arbitrary constant degree over classical neural networks in performing a classical sequence modeling task. Furthermore, each unit cell of the introduced class of QNNs is computationally efficient, implementable in constant time on a quantum device. The classical networks we prove a separation over include well-known examples such as recurrent neural networks and Transformers. We show that quantum contextuality is the source of the expressivity separation, suggesting that other classical sequence learning problems with long-time correlations may be a regime where practical advantages in quantum machine learning may exist.

Does provable absence of barren plateaus imply classical simulability? Or, why we need to rethink variational quantum computing

A large amount of effort has recently been put into understanding the barren plateau phenomenon. In this perspective article, we face the increasingly loud elephant in the room and ask a question that has been hinted at by many but not explicitly addressed: Can the structure that allows one to avoid barren plateaus also be leveraged to efficiently simulate the loss classically? We present strong evidence that commonly used models with provable absence of barren plateaus are also classically simulable, provided that one can collect some classical data from quantum devices during an initial data acquisition phase. This follows from the observation that barren plateaus result from a curse of dimensionality, and that current approaches for solving them end up encoding the problem into some small, classically simulable, subspaces. This sheds serious doubt on the non-classicality of the information processing capabilities of parametrized quantum circuits for barren plateau-free landscapes and on the possibility of superpolynomial advantages from running them on quantum hardware. We end by discussing caveats in our arguments, the role of smart initializations, and by highlighting new opportunities that our perspective raises.

Enhancing Generative Models via Quantum Correlations

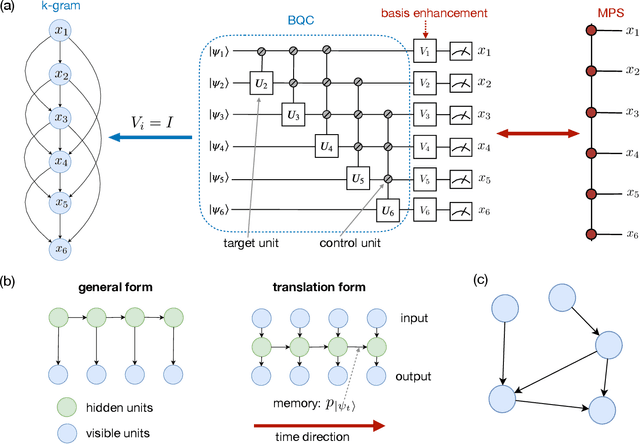
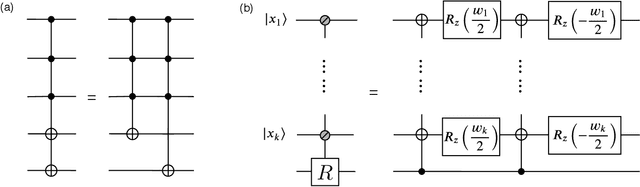
Generative modeling using samples drawn from the probability distribution constitutes a powerful approach for unsupervised machine learning. Quantum mechanical systems can produce probability distributions that exhibit quantum correlations which are difficult to capture using classical models. We show theoretically that such quantum correlations provide a powerful resource for generative modeling. In particular, we provide an unconditional proof of separation in expressive power between a class of widely-used generative models, known as Bayesian networks, and its minimal quantum extension. We show that this expressivity advantage is associated with quantum nonlocality and quantum contextuality. Furthermore, we numerically test this separation on standard machine learning data sets and show that it holds for practical problems. The possibility of quantum advantage demonstrated in this work not only sheds light on the design of useful quantum machine learning protocols but also provides inspiration to draw on ideas from quantum foundations to improve purely classical algorithms.

Coreset Clustering on Small Quantum Computers

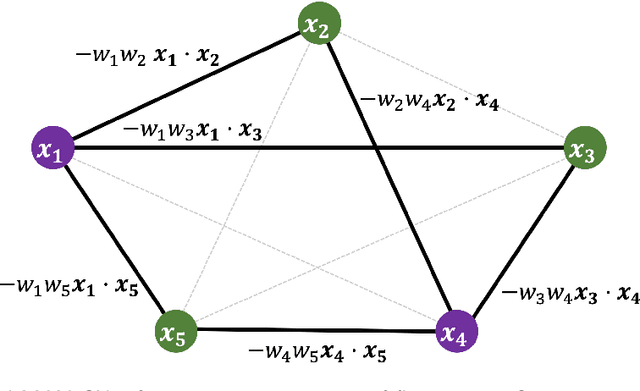
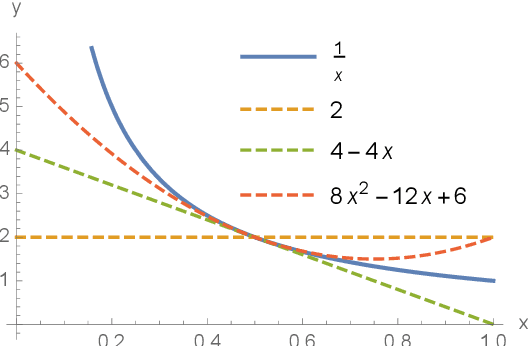
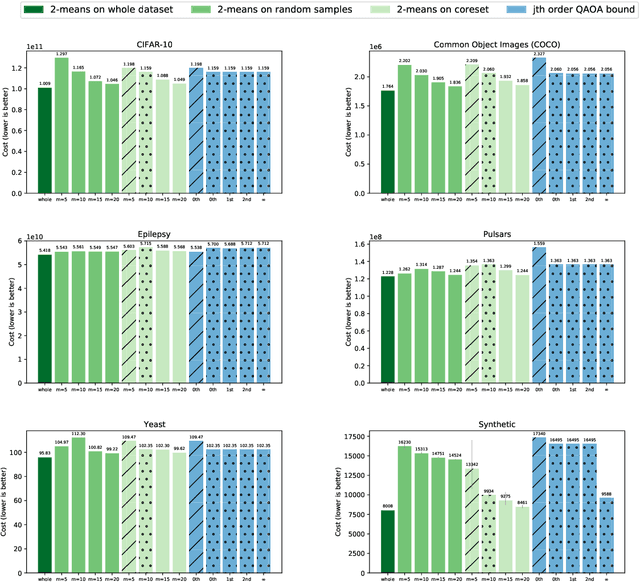
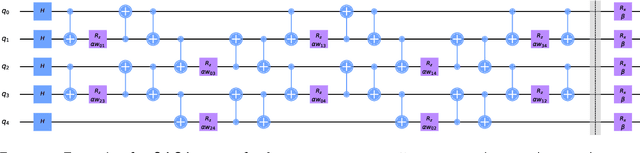
Many quantum algorithms for machine learning require access to classical data in superposition. However, for many natural data sets and algorithms, the overhead required to load the data set in superposition can erase any potential quantum speedup over classical algorithms. Recent work by Harrow introduces a new paradigm in hybrid quantum-classical computing to address this issue, relying on coresets to minimize the data loading overhead of quantum algorithms. We investigate using this paradigm to perform $k$-means clustering on near-term quantum computers, by casting it as a QAOA optimization instance over a small coreset. We compare the performance of this approach to classical $k$-means clustering both numerically and experimentally on IBM Q hardware. We are able to find data sets where coresets work well relative to random sampling and where QAOA could potentially outperform standard $k$-means on a coreset. However, finding data sets where both coresets and QAOA work well--which is necessary for a quantum advantage over $k$-means on the entire data set--appears to be challenging.

Near-Term Quantum-Classical Associative Adversarial Networks

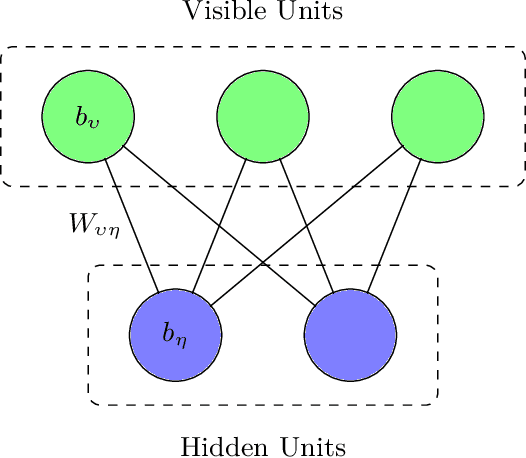
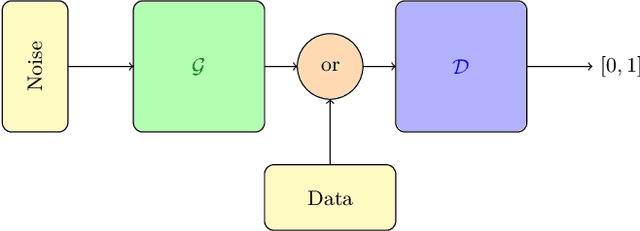
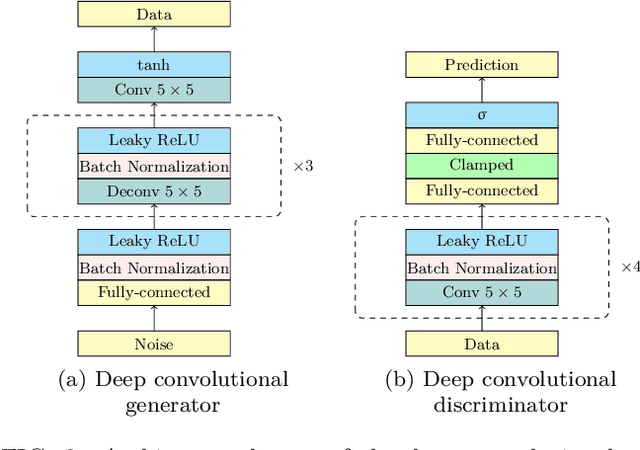
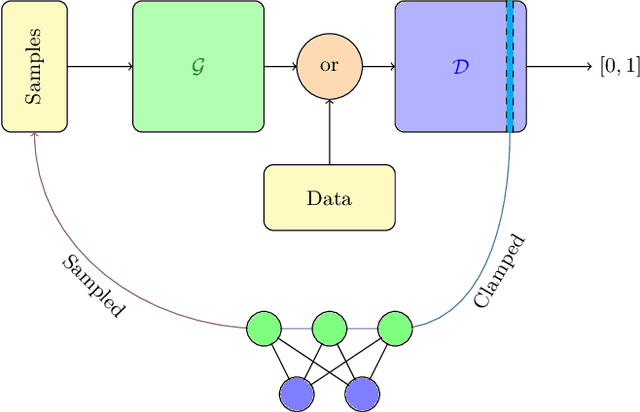
We introduce a new hybrid quantum-classical adversarial machine learning architecture called a quantum-classical associative adversarial network (QAAN). This architecture consists of a classical generative adversarial network with a small auxiliary quantum Boltzmann machine that is simultaneously trained on an intermediate layer of the discriminator of the generative network. We numerically study the performance of QAANs compared to their classical counterparts on the MNIST and CIFAR-10 data sets, and show that QAANs attain a higher quality of learning when evaluated using the Inception score and the Fr\'{e}chet Inception distance. As the QAAN architecture only relies on sampling simple local observables of a small quantum Boltzmann machine, this model is particularly amenable for implementation on the current and next generations of quantum devices.