Architectures and random properties of symplectic quantum circuits

Parametrized and random unitary (or orthogonal) $n$-qubit circuits play a central role in quantum information. As such, one could naturally assume that circuits implementing symplectic transformation would attract similar attention. However, this is not the case, as $\mathbb{SP}(d/2)$ -- the group of $d\times d$ unitary symplectic matrices -- has thus far been overlooked. In this work, we aim at starting to right this wrong. We begin by presenting a universal set of generators $\mathcal{G}$ for the symplectic algebra $i\mathfrak{sp}(d/2)$, consisting of one- and two-qubit Pauli operators acting on neighboring sites in a one-dimensional lattice. Here, we uncover two critical differences between such set, and equivalent ones for unitary and orthogonal circuits. Namely, we find that the operators in $\mathcal{G}$ cannot generate arbitrary local symplectic unitaries and that they are not translationally invariant. We then review the Schur-Weyl duality between the symplectic group and the Brauer algebra, and use tools from Weingarten calculus to prove that Pauli measurements at the output of Haar random symplectic circuits can converge to Gaussian processes. As a by-product, such analysis provides us with concentration bounds for Pauli measurements in circuits that form $t$-designs over $\mathbb{SP}(d/2)$. To finish, we present tensor-network tools to analyze shallow random symplectic circuits, and we use these to numerically show that computational-basis measurements anti-concentrate at logarithmic depth.

Does provable absence of barren plateaus imply classical simulability? Or, why we need to rethink variational quantum computing

A large amount of effort has recently been put into understanding the barren plateau phenomenon. In this perspective article, we face the increasingly loud elephant in the room and ask a question that has been hinted at by many but not explicitly addressed: Can the structure that allows one to avoid barren plateaus also be leveraged to efficiently simulate the loss classically? We present strong evidence that commonly used models with provable absence of barren plateaus are also classically simulable, provided that one can collect some classical data from quantum devices during an initial data acquisition phase. This follows from the observation that barren plateaus result from a curse of dimensionality, and that current approaches for solving them end up encoding the problem into some small, classically simulable, subspaces. This sheds serious doubt on the non-classicality of the information processing capabilities of parametrized quantum circuits for barren plateau-free landscapes and on the possibility of superpolynomial advantages from running them on quantum hardware. We end by discussing caveats in our arguments, the role of smart initializations, and by highlighting new opportunities that our perspective raises.

Deep quantum neural networks form Gaussian processes

It is well known that artificial neural networks initialized from independent and identically distributed priors converge to Gaussian processes in the limit of large number of neurons per hidden layer. In this work we prove an analogous result for Quantum Neural Networks (QNNs). Namely, we show that the outputs of certain models based on Haar random unitary or orthogonal deep QNNs converge to Gaussian processes in the limit of large Hilbert space dimension $d$. The derivation of this result is more nuanced than in the classical case due the role played by the input states, the measurement observable, and the fact that the entries of unitary matrices are not independent. An important consequence of our analysis is that the ensuing Gaussian processes cannot be used to efficiently predict the outputs of the QNN via Bayesian statistics. Furthermore, our theorems imply that the concentration of measure phenomenon in Haar random QNNs is much worse than previously thought, as we prove that expectation values and gradients concentrate as $\mathcal{O}\left(\frac{1}{e^d \sqrt{d}}\right)$ -- exponentially in the Hilbert space dimension. Finally, we discuss how our results improve our understanding of concentration in $t$-designs.

Effects of noise on the overparametrization of quantum neural networks

Overparametrization is one of the most surprising and notorious phenomena in machine learning. Recently, there have been several efforts to study if, and how, Quantum Neural Networks (QNNs) acting in the absence of hardware noise can be overparametrized. In particular, it has been proposed that a QNN can be defined as overparametrized if it has enough parameters to explore all available directions in state space. That is, if the rank of the Quantum Fisher Information Matrix (QFIM) for the QNN's output state is saturated. Here, we explore how the presence of noise affects the overparametrization phenomenon. Our results show that noise can "turn on" previously-zero eigenvalues of the QFIM. This enables the parametrized state to explore directions that were otherwise inaccessible, thus potentially turning an overparametrized QNN into an underparametrized one. For small noise levels, the QNN is quasi-overparametrized, as large eigenvalues coexists with small ones. Then, we prove that as the magnitude of noise increases all the eigenvalues of the QFIM become exponentially suppressed, indicating that the state becomes insensitive to any change in the parameters. As such, there is a pull-and-tug effect where noise can enable new directions, but also suppress the sensitivity to parameter updates. Finally, our results imply that current QNN capacity measures are ill-defined when hardware noise is present.

Theory of overparametrization in quantum neural networks

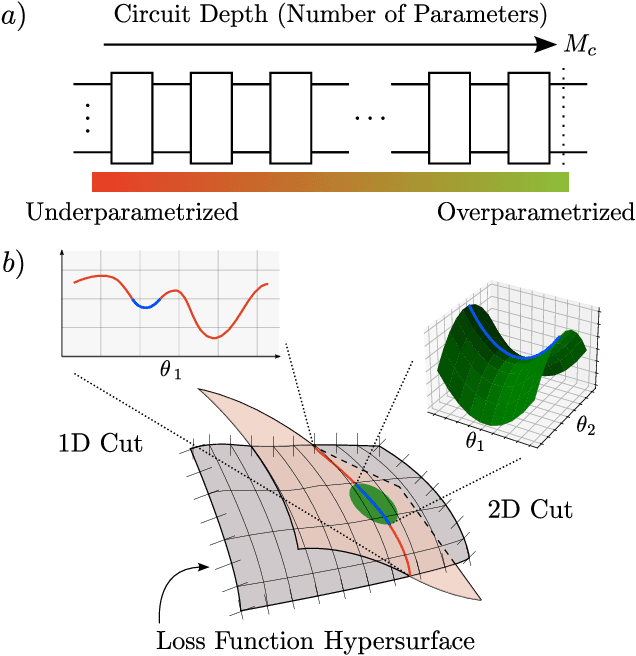
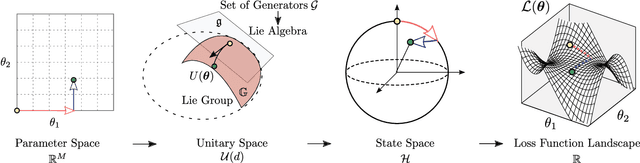
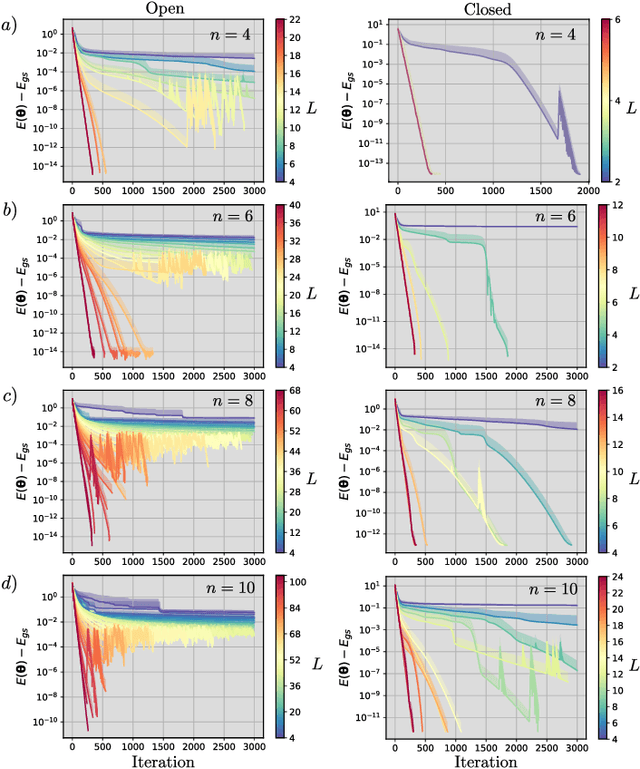
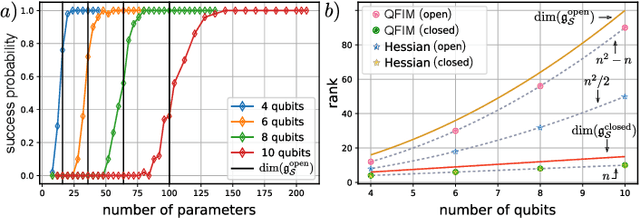
The prospect of achieving quantum advantage with Quantum Neural Networks (QNNs) is exciting. Understanding how QNN properties (e.g., the number of parameters $M$) affect the loss landscape is crucial to the design of scalable QNN architectures. Here, we rigorously analyze the overparametrization phenomenon in QNNs with periodic structure. We define overparametrization as the regime where the QNN has more than a critical number of parameters $M_c$ that allows it to explore all relevant directions in state space. Our main results show that the dimension of the Lie algebra obtained from the generators of the QNN is an upper bound for $M_c$, and for the maximal rank that the quantum Fisher information and Hessian matrices can reach. Underparametrized QNNs have spurious local minima in the loss landscape that start disappearing when $M\geq M_c$. Thus, the overparametrization onset corresponds to a computational phase transition where the QNN trainability is greatly improved by a more favorable landscape. We then connect the notion of overparametrization to the QNN capacity, so that when a QNN is overparametrized, its capacity achieves its maximum possible value. We run numerical simulations for eigensolver, compilation, and autoencoding applications to showcase the overparametrization computational phase transition. We note that our results also apply to variational quantum algorithms and quantum optimal control.

Qibo: a framework for quantum simulation with hardware acceleration

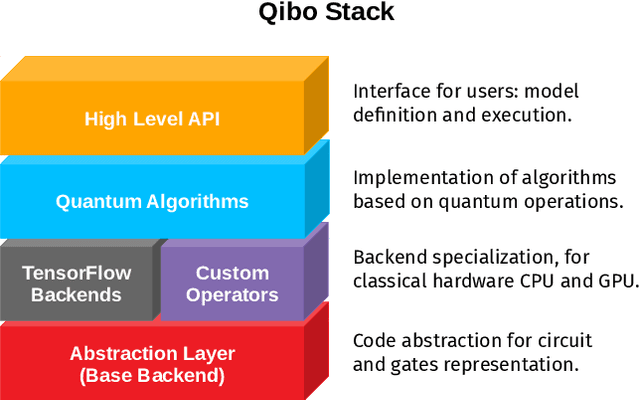
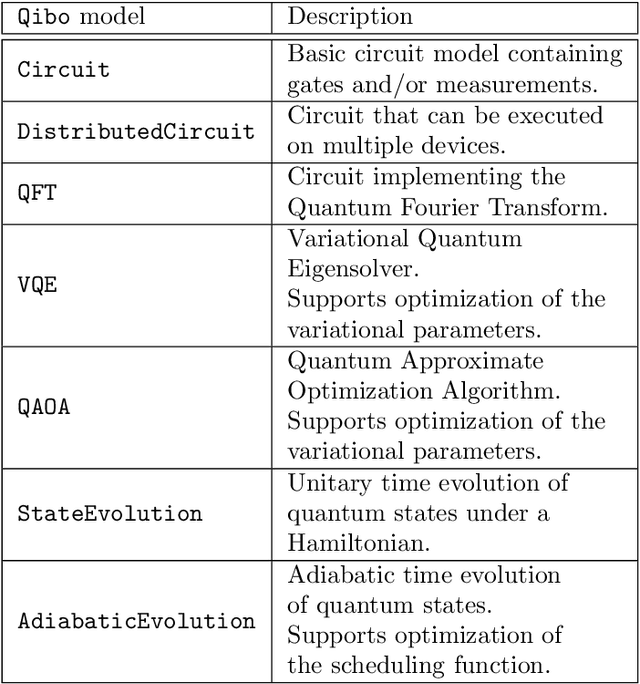
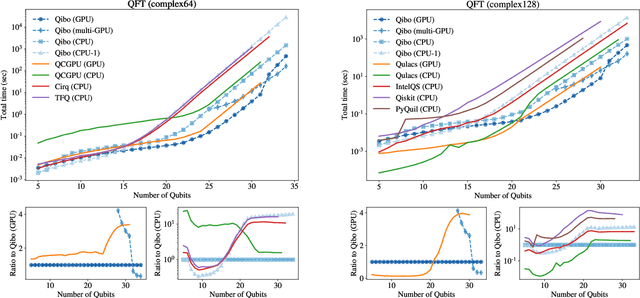
We present Qibo, a new open-source software for fast evaluation of quantum circuits and adiabatic evolution which takes full advantage of hardware accelerators. The growing interest in quantum computing and the recent developments of quantum hardware devices motivates the development of new advanced computational tools focused on performance and usage simplicity. In this work we introduce a new quantum simulation framework that enables developers to delegate all complicated aspects of hardware or platform implementation to the library so they can focus on the problem and quantum algorithms at hand. This software is designed from scratch with simulation performance, code simplicity and user friendly interface as target goals. It takes advantage of hardware acceleration such as multi-threading CPU, single GPU and multi-GPU devices.