Non-Parametric Cluster Significance Testing with Reference to a Unimodal Null Distribution

Cluster analysis is an unsupervised learning strategy that can be employed to identify subgroups of observations in data sets of unknown structure. This strategy is particularly useful for analyzing high-dimensional data such as microarray gene expression data. Many clustering methods are available, but it is challenging to determine if the identified clusters represent distinct subgroups. We propose a novel strategy to investigate the significance of identified clusters by comparing the within- cluster sum of squares from the original data to that produced by clustering an appropriate unimodal null distribution. The null distribution we present for this problem uses kernel density estimation and thus does not require that the data follow any particular distribution. We find that our method can accurately test for the presence of clustering even when the number of features is high.

Identification of relevant subtypes via preweighted sparse clustering

Cluster analysis methods are used to identify homogeneous subgroups in a data set. In biomedical applications, one frequently applies cluster analysis in order to identify biologically interesting subgroups. In particular, one may wish to identify subgroups that are associated with a particular outcome of interest. Conventional clustering methods generally do not identify such subgroups, particularly when there are a large number of high-variance features in the data set. Conventional methods may identify clusters associated with these high-variance features when one wishes to obtain secondary clusters that are more interesting biologically or more strongly associated with a particular outcome of interest. A modification of sparse clustering can be used to identify such secondary clusters or clusters associated with an outcome of interest. This method correctly identifies such clusters of interest in several simulation scenarios. The method is also applied to a large prospective cohort study of temporomandibular disorders and a leukemia microarray data set.

Biclustering Via Sparse Clustering

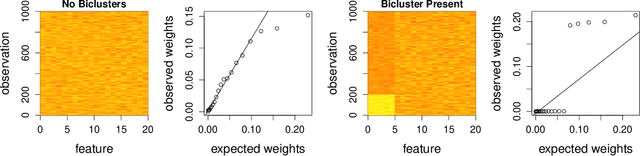
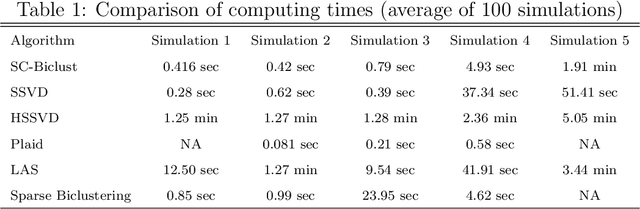
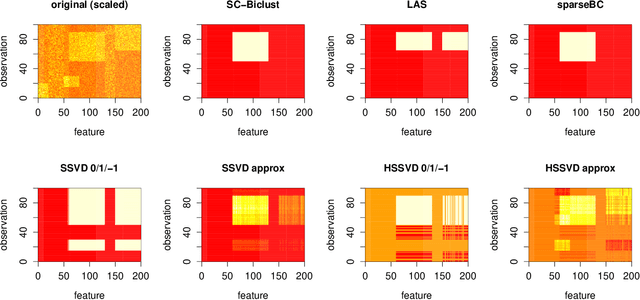
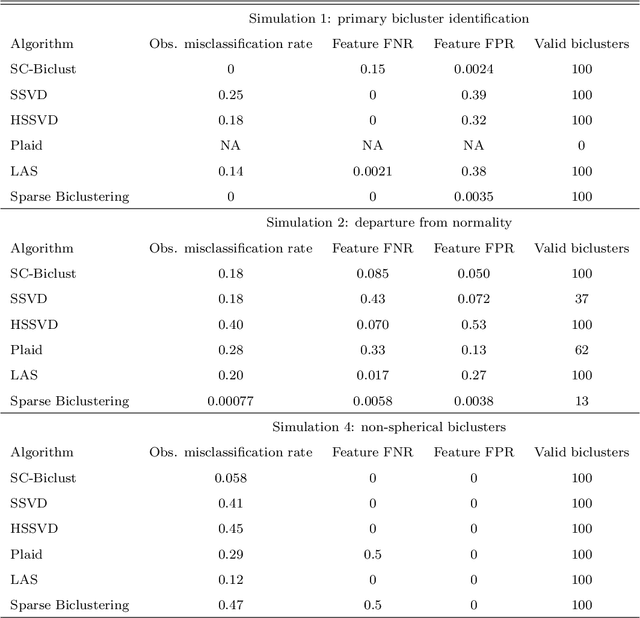
In many situations it is desirable to identify clusters that differ with respect to only a subset of features. Such clusters may represent homogeneous subgroups of patients with a disease, such as cancer or chronic pain. We define a bicluster to be a submatrix U of a larger data matrix X such that the features and observations in U differ from those not contained in U. For example, the observations in U could have different means or variances with respect to the features in U. We propose a general framework for biclustering based on the sparse clustering method of Witten and Tibshirani (2010). We develop a method for identifying features that belong to biclusters. This framework can be used to identify biclusters that differ with respect to the means of the features, the variance of the features, or more general differences. We apply these methods to several simulated and real-world data sets and compare the results of our method with several previously published methods. The results of our method compare favorably with existing methods with respect to both predictive accuracy and computing time.

Semi-supervised clustering methods

Cluster analysis methods seek to partition a data set into homogeneous subgroups. It is useful in a wide variety of applications, including document processing and modern genetics. Conventional clustering methods are unsupervised, meaning that there is no outcome variable nor is anything known about the relationship between the observations in the data set. In many situations, however, information about the clusters is available in addition to the values of the features. For example, the cluster labels of some observations may be known, or certain observations may be known to belong to the same cluster. In other cases, one may wish to identify clusters that are associated with a particular outcome variable. This review describes several clustering algorithms (known as "semi-supervised clustering" methods) that can be applied in these situations. The majority of these methods are modifications of the popular k-means clustering method, and several of them will be described in detail. A brief description of some other semi-supervised clustering algorithms is also provided.