Toward Deeper Understanding of Nonconvex Stochastic Optimization with Momentum using Diffusion Approximations

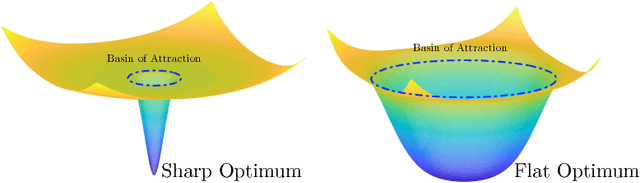
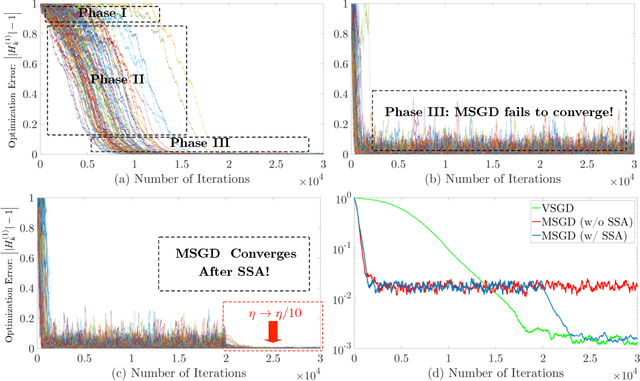
Momentum Stochastic Gradient Descent (MSGD) algorithm has been widely applied to many nonconvex optimization problems in machine learning. Popular examples include training deep neural networks, dimensionality reduction, and etc. Due to the lack of convexity and the extra momentum term, the optimization theory of MSGD is still largely unknown. In this paper, we study this fundamental optimization algorithm based on the so-called "strict saddle problem." By diffusion approximation type analysis, our study shows that the momentum helps escape from saddle points, but hurts the convergence within the neighborhood of optima (if without the step size annealing). Our theoretical discovery partially corroborates the empirical success of MSGD in training deep neural networks. Moreover, our analysis applies the martingale method and "Fixed-State-Chain" method from the stochastic approximation literature, which are of independent interest.

Towards Understanding Acceleration Tradeoff between Momentum and Asynchrony in Nonconvex Stochastic Optimization

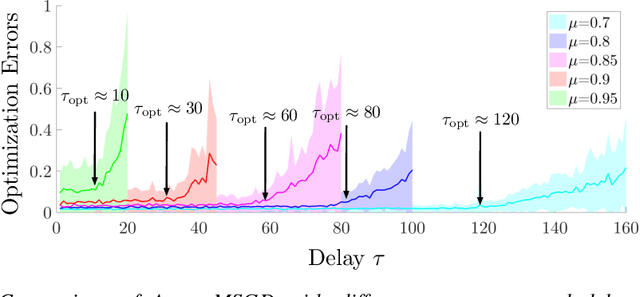
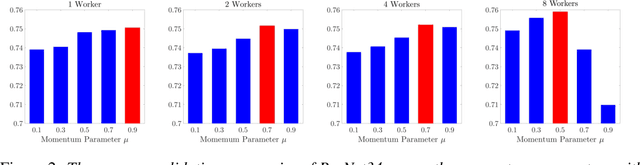
Asynchronous momentum stochastic gradient descent algorithms (Async-MSGD) is one of the most popular algorithms in distributed machine learning. However, its convergence properties for these complicated nonconvex problems is still largely unknown, because of the current technical limit. Therefore, in this paper, we propose to analyze the algorithm through a simpler but nontrivial nonconvex problem - streaming PCA, which helps us to understand Aync-MSGD better even for more general problems. Specifically, we establish the asymptotic rate of convergence of Async-MSGD for streaming PCA by diffusion approximation. Our results indicate a fundamental tradeoff between asynchrony and momentum: To ensure convergence and acceleration through asynchrony, we have to reduce the momentum (compared with Sync-MSGD). To the best of our knowledge, this is the first theoretical attempt on understanding Async-MSGD for distributed nonconvex stochastic optimization. Numerical experiments on both streaming PCA and training deep neural networks are provided to support our findings for Async-MSGD.