Reversible Architectures for Arbitrarily Deep Residual Neural Networks

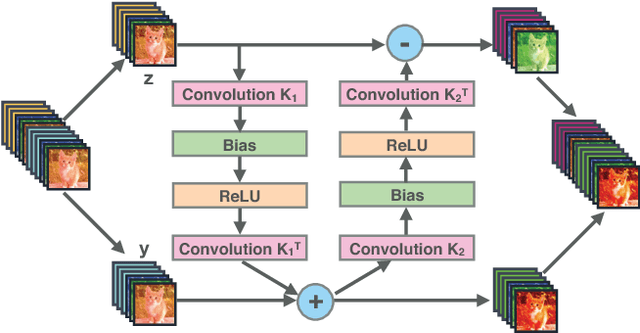
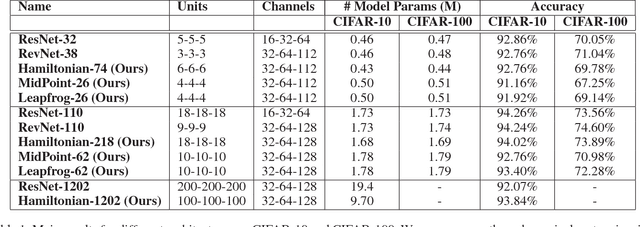
Recently, deep residual networks have been successfully applied in many computer vision and natural language processing tasks, pushing the state-of-the-art performance with deeper and wider architectures. In this work, we interpret deep residual networks as ordinary differential equations (ODEs), which have long been studied in mathematics and physics with rich theoretical and empirical success. From this interpretation, we develop a theoretical framework on stability and reversibility of deep neural networks, and derive three reversible neural network architectures that can go arbitrarily deep in theory. The reversibility property allows a memory-efficient implementation, which does not need to store the activations for most hidden layers. Together with the stability of our architectures, this enables training deeper networks using only modest computational resources. We provide both theoretical analyses and empirical results. Experimental results demonstrate the efficacy of our architectures against several strong baselines on CIFAR-10, CIFAR-100 and STL-10 with superior or on-par state-of-the-art performance. Furthermore, we show our architectures yield superior results when trained using fewer training data.

Learning across scales - A multiscale method for Convolution Neural Networks

In this work we establish the relation between optimal control and training deep Convolution Neural Networks (CNNs). We show that the forward propagation in CNNs can be interpreted as a time-dependent nonlinear differential equation and learning as controlling the parameters of the differential equation such that the network approximates the data-label relation for given training data. Using this continuous interpretation we derive two new methods to scale CNNs with respect to two different dimensions. The first class of multiscale methods connects low-resolution and high-resolution data through prolongation and restriction of CNN parameters. We demonstrate that this enables classifying high-resolution images using CNNs trained with low-resolution images and vice versa and warm-starting the learning process. The second class of multiscale methods connects shallow and deep networks and leads to new training strategies that gradually increase the depths of the CNN while re-using parameters for initializations.