PRIMG : Efficient LLM-driven Test Generation Using Mutant Prioritization

Mutation testing is a widely recognized technique for assessing and enhancing the effectiveness of software test suites by introducing deliberate code mutations. However, its application often results in overly large test suites, as developers generate numerous tests to kill specific mutants, increasing computational overhead. This paper introduces PRIMG (Prioritization and Refinement Integrated Mutation-driven Generation), a novel framework for incremental and adaptive test case generation for Solidity smart contracts. PRIMG integrates two core components: a mutation prioritization module, which employs a machine learning model trained on mutant subsumption graphs to predict the usefulness of surviving mutants, and a test case generation module, which utilizes Large Language Models (LLMs) to generate and iteratively refine test cases to achieve syntactic and behavioral correctness. We evaluated PRIMG on real-world Solidity projects from Code4Arena to assess its effectiveness in improving mutation scores and generating high-quality test cases. The experimental results demonstrate that PRIMG significantly reduces test suite size while maintaining high mutation coverage. The prioritization module consistently outperformed random mutant selection, enabling the generation of high-impact tests with reduced computational effort. Furthermore, the refining process enhanced the correctness and utility of LLM-generated tests, addressing their inherent limitations in handling edge cases and complex program logic.

Relating Complexity-theoretic Parameters with SAT Solver Performance

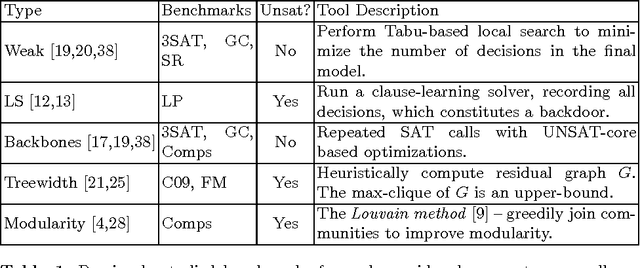
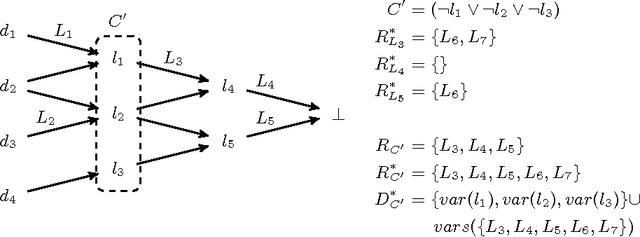
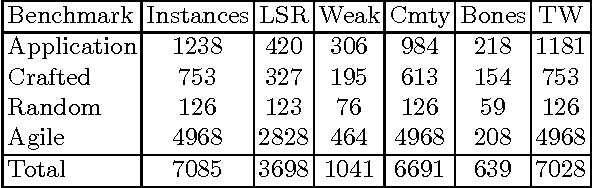
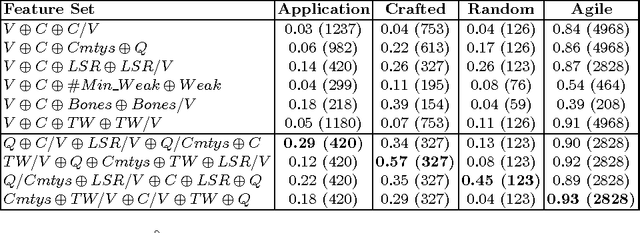
Over the years complexity theorists have proposed many structural parameters to explain the surprising efficiency of conflict-driven clause-learning (CDCL) SAT solvers on a wide variety of large industrial Boolean instances. While some of these parameters have been studied empirically, until now there has not been a unified comparative study of their explanatory power on a comprehensive benchmark. We correct this state of affairs by conducting a large-scale empirical evaluation of CDCL SAT solver performance on nearly 7000 industrial and crafted formulas against several structural parameters such as backdoors, treewidth, backbones, and community structure. Our study led us to several results. First, we show that while such parameters only weakly correlate with CDCL solving time, certain combinations of them yield much better regression models. Second, we show how some parameters can be used as a "lens" to better understand the efficiency of different solving heuristics. Finally, we propose a new complexity-theoretic parameter, which we call learning-sensitive with restarts (LSR) backdoors, that extends the notion of learning-sensitive (LS) backdoors to incorporate restarts and discuss algorithms to compute them. We mathematically prove that for certain class of instances minimal LSR-backdoors are exponentially smaller than minimal-LS backdoors.