Discovering Symmetry Group Structures via Implicit Orthogonality Bias

We introduce the HyperCube network, a novel approach for autonomously discovering symmetry group structures within data. The key innovation is a unique factorization architecture coupled with a novel regularizer that instills a powerful inductive bias towards learning orthogonal representations. This leverages a fundamental theorem of representation theory that all compact/finite groups can be represented by orthogonal matrices. HyperCube efficiently learns general group operations from partially observed data, successfully recovering complete operation tables. Remarkably, the learned factors correspond directly to exact matrix representations of the underlying group. Moreover, these factors capture the group's complete set of irreducible representations, forming the generalized Fourier basis for performing group convolutions. In extensive experiments with both group and non-group symbolic operations, HyperCube demonstrates a dramatic 100-1000x improvement in training speed and 2-10x greater sample efficiency compared to the Transformer baseline. These results suggest that our approach unlocks a new class of deep learning models capable of harnessing inherent symmetries within data, leading to significant improvements in performance and broader applicability.

ISAAC Newton: Input-based Approximate Curvature for Newton's Method

We present ISAAC (Input-baSed ApproximAte Curvature), a novel method that conditions the gradient using selected second-order information and has an asymptotically vanishing computational overhead, assuming a batch size smaller than the number of neurons. We show that it is possible to compute a good conditioner based on only the input to a respective layer without a substantial computational overhead. The proposed method allows effective training even in small-batch stochastic regimes, which makes it competitive to first-order as well as second-order methods.

The Missing Invariance Principle Found -- the Reciprocal Twin of Invariant Risk Minimization

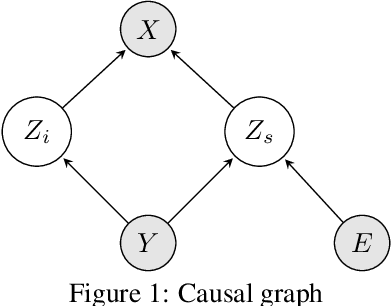
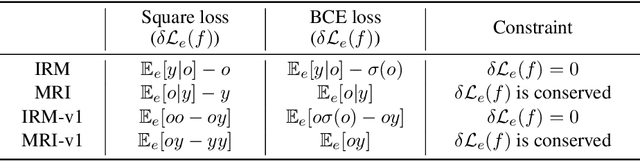
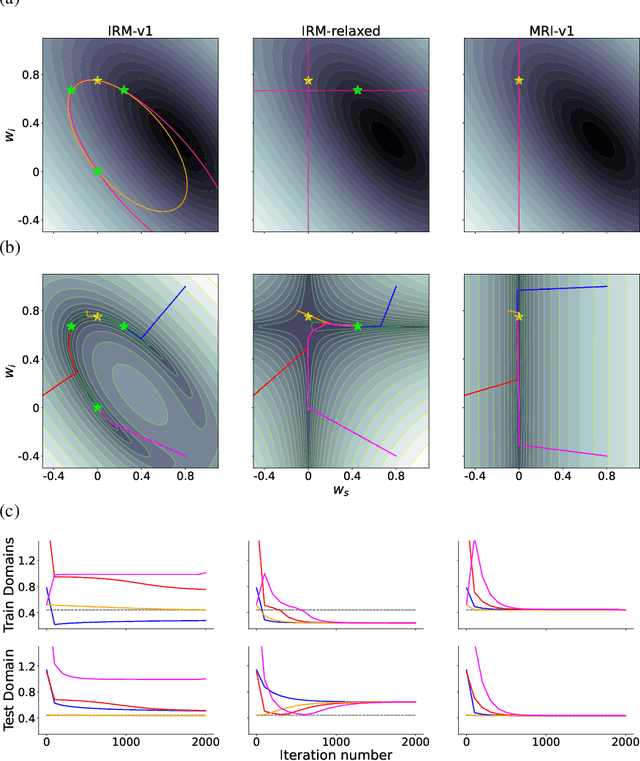
Machine learning models often generalize poorly to out-of-distribution (OOD) data as a result of relying on features that are spuriously correlated with the label during training. Recently, the technique of Invariant Risk Minimization (IRM) was proposed to learn predictors that only use invariant features by conserving the feature-conditioned class expectation $\mathbb{E}_e[y|f(x)]$ across environments. However, more recent studies have demonstrated that IRM can fail in various task settings. Here, we identify a fundamental flaw of IRM formulation that causes the failure. We then introduce a complementary notion of invariance, MRI, that is based on conserving the class-conditioned feature expectation $\mathbb{E}_e[f(x)|y]$ across environments, that corrects for the flaw in IRM. Further, we introduce a simplified, practical version of the MRI formulation called as MRI-v1. We note that this constraint is convex which confers it with an advantage over the practical version of IRM, IRM-v1, which imposes non-convex constraints. We prove that in a general linear problem setting, MRI-v1 can guarantee invariant predictors given sufficient environments. We also empirically demonstrate that MRI strongly out-performs IRM and consistently achieves near-optimal OOD generalization in image-based nonlinear problems.

Gradient Descent for Spiking Neural Networks

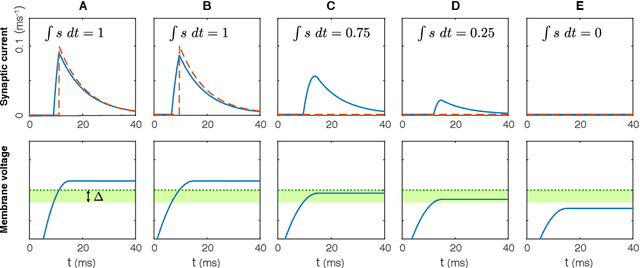
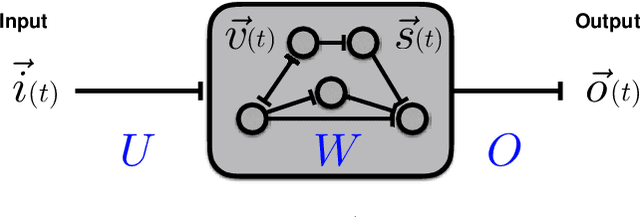
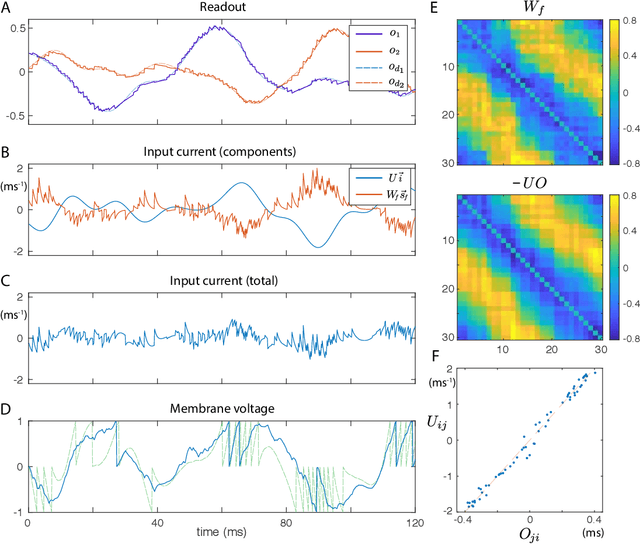
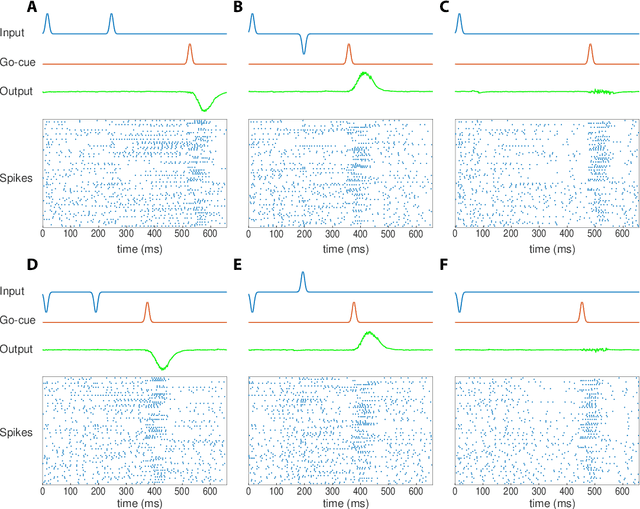
Much of studies on neural computation are based on network models of static neurons that produce analog output, despite the fact that information processing in the brain is predominantly carried out by dynamic neurons that produce discrete pulses called spikes. Research in spike-based computation has been impeded by the lack of efficient supervised learning algorithm for spiking networks. Here, we present a gradient descent method for optimizing spiking network models by introducing a differentiable formulation of spiking networks and deriving the exact gradient calculation. For demonstration, we trained recurrent spiking networks on two dynamic tasks: one that requires optimizing fast (~millisecond) spike-based interactions for efficient encoding of information, and a delayed memory XOR task over extended duration (~second). The results show that our method indeed optimizes the spiking network dynamics on the time scale of individual spikes as well as behavioral time scales. In conclusion, our result offers a general purpose supervised learning algorithm for spiking neural networks, thus advancing further investigations on spike-based computation.

The Vector Space of Convex Curves: How to Mix Shapes

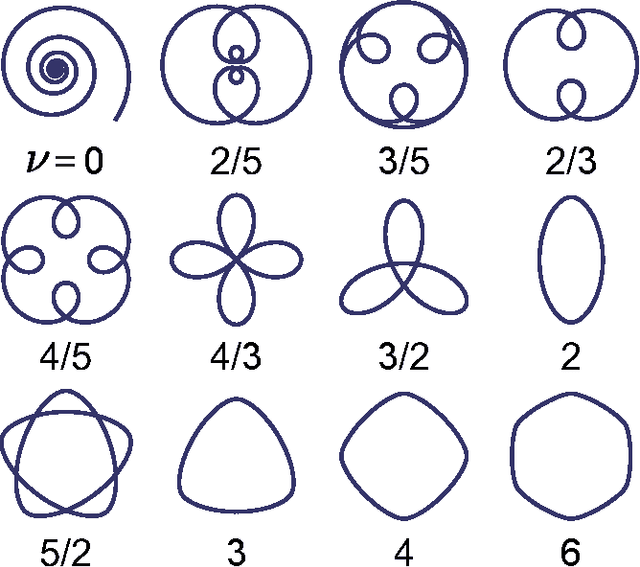
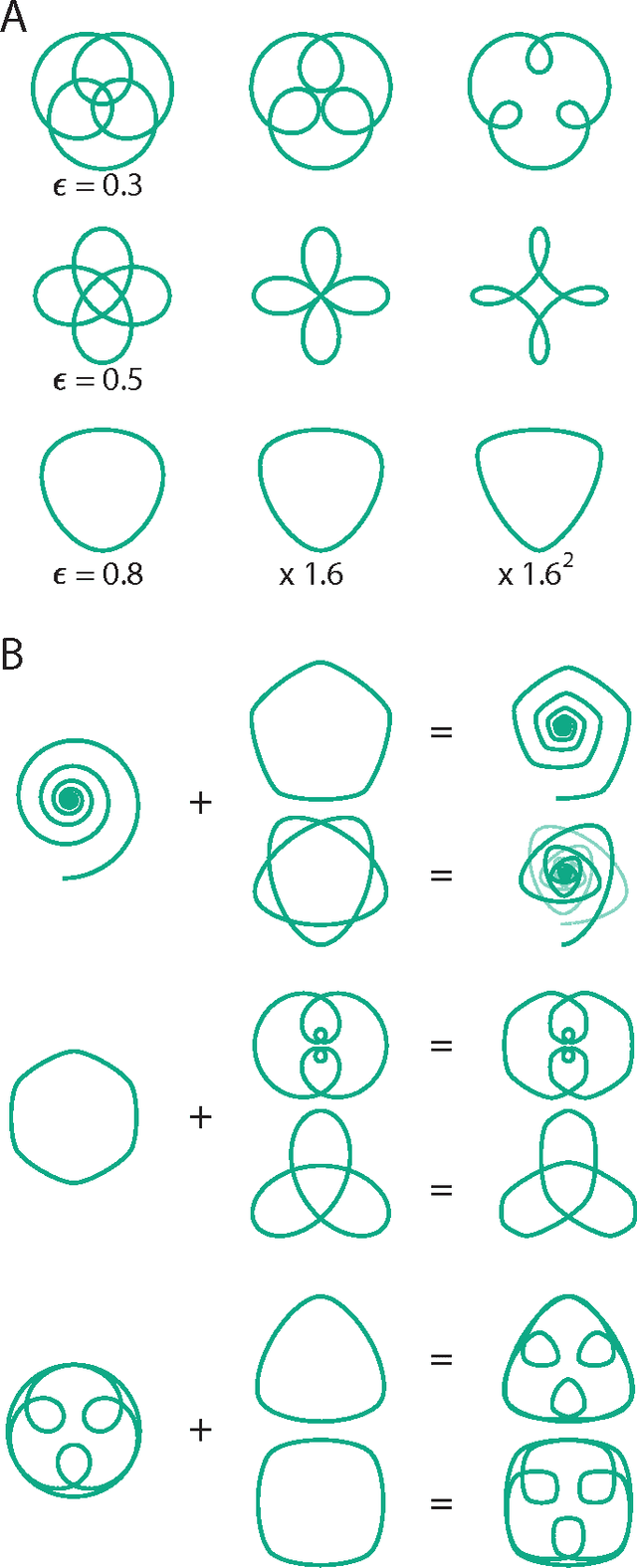
We present a novel, log-radius profile representation for convex curves and define a new operation for combining the shape features of curves. Unlike the standard, angle profile-based methods, this operation accurately combines the shape features in a visually intuitive manner. This method have implications in shape analysis as well as in investigating how the brain perceives and generates curved shapes and motions.