Multidimensional Interpolants

In the domain of differential equation-based generative modeling, conventional approaches often rely on single-dimensional scalar values as interpolation coefficients during both training and inference phases. In this work, we introduce, for the first time, a multidimensional interpolant that extends these coefficients into multiple dimensions, leveraging the stochastic interpolant framework. Additionally, we propose a novel path optimization problem tailored to adaptively determine multidimensional inference trajectories, with a predetermined differential equation solver and a fixed number of function evaluations. Our solution involves simulation dynamics coupled with adversarial training to optimize the inference path. Notably, employing a multidimensional interpolant during training improves the model's inference performance, even in the absence of path optimization. When the adaptive, multidimensional path derived from our optimization process is employed, it yields further performance gains, even with fixed solver configurations. The introduction of multidimensional interpolants not only enhances the efficacy of models but also opens up a new domain for exploration in training and inference methodologies, emphasizing the potential of multidimensional paths as an untapped frontier.

SPGP: Structure Prototype Guided Graph Pooling

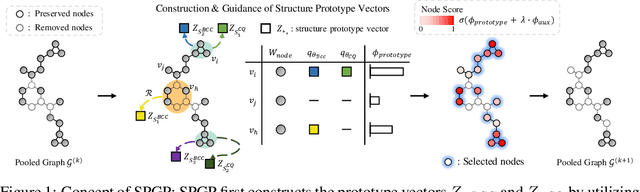
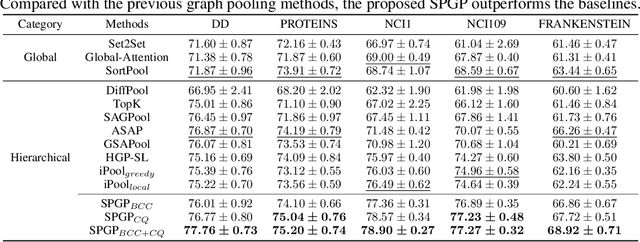
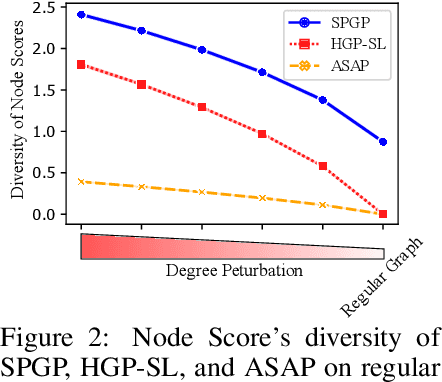
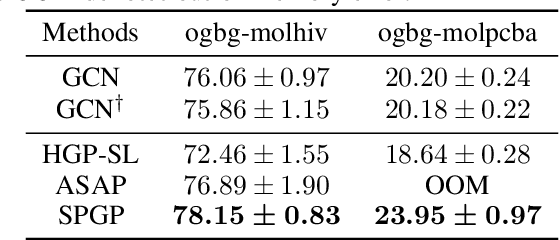
While graph neural networks (GNNs) have been successful for node classification tasks and link prediction tasks in graph, learning graph-level representations still remains a challenge. For the graph-level representation, it is important to learn both representation of neighboring nodes, i.e., aggregation, and graph structural information. A number of graph pooling methods have been developed for this goal. However, most of the existing pooling methods utilize k-hop neighborhood without considering explicit structural information in a graph. In this paper, we propose Structure Prototype Guided Pooling (SPGP) that utilizes prior graph structures to overcome the limitation. SPGP formulates graph structures as learnable prototype vectors and computes the affinity between nodes and prototype vectors. This leads to a novel node scoring scheme that prioritizes informative nodes while encapsulating the useful structures of the graph. Our experimental results show that SPGP outperforms state-of-the-art graph pooling methods on graph classification benchmark datasets in both accuracy and scalability.

Sparse Structure Learning via Graph Neural Networks for Inductive Document Classification

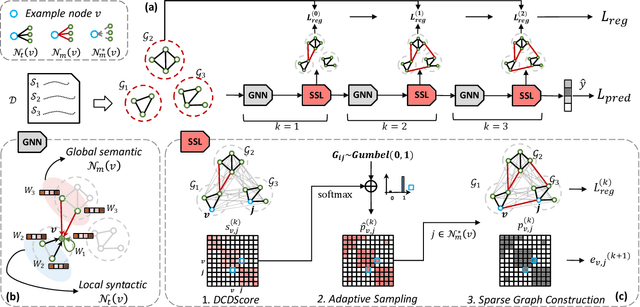
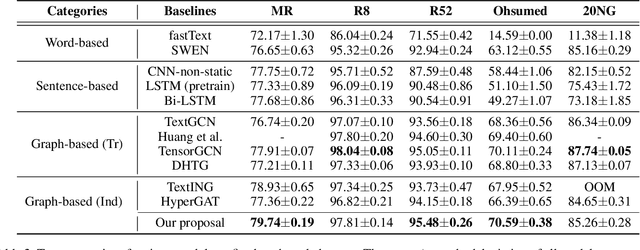
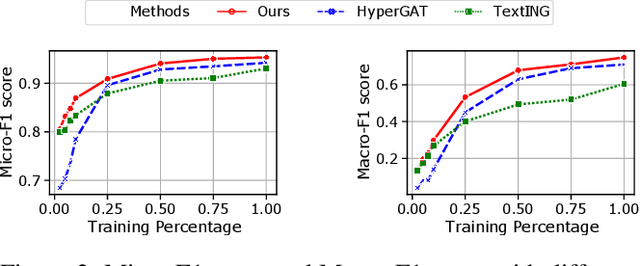
Recently, graph neural networks (GNNs) have been widely used for document classification. However, most existing methods are based on static word co-occurrence graphs without sentence-level information, which poses three challenges:(1) word ambiguity, (2) word synonymity, and (3) dynamic contextual dependency. To address these challenges, we propose a novel GNN-based sparse structure learning model for inductive document classification. Specifically, a document-level graph is initially generated by a disjoint union of sentence-level word co-occurrence graphs. Our model collects a set of trainable edges connecting disjoint words between sentences and employs structure learning to sparsely select edges with dynamic contextual dependencies. Graphs with sparse structures can jointly exploit local and global contextual information in documents through GNNs. For inductive learning, the refined document graph is further fed into a general readout function for graph-level classification and optimization in an end-to-end manner. Extensive experiments on several real-world datasets demonstrate that the proposed model outperforms most state-of-the-art results, and reveal the necessity to learn sparse structures for each document.