Space-Time Continuous PDE Forecasting using Equivariant Neural Fields

Recently, Conditional Neural Fields (NeFs) have emerged as a powerful modelling paradigm for PDEs, by learning solutions as flows in the latent space of the Conditional NeF. Although benefiting from favourable properties of NeFs such as grid-agnosticity and space-time-continuous dynamics modelling, this approach limits the ability to impose known constraints of the PDE on the solutions -- e.g. symmetries or boundary conditions -- in favour of modelling flexibility. Instead, we propose a space-time continuous NeF-based solving framework that - by preserving geometric information in the latent space - respects known symmetries of the PDE. We show that modelling solutions as flows of pointclouds over the group of interest $G$ improves generalization and data-efficiency. We validated that our framework readily generalizes to unseen spatial and temporal locations, as well as geometric transformations of the initial conditions - where other NeF-based PDE forecasting methods fail - and improve over baselines in a number of challenging geometries.

Neural Modulation Fields for Conditional Cone Beam Neural Tomography

Conventional Computed Tomography (CT) methods require large numbers of noise-free projections for accurate density reconstructions, limiting their applicability to the more complex class of Cone Beam Geometry CT (CBCT) reconstruction. Recently, deep learning methods have been proposed to overcome these limitations, with methods based on neural fields (NF) showing strong performance, by approximating the reconstructed density through a continuous-in-space coordinate based neural network. Our focus is on improving such methods, however, unlike previous work, which requires training an NF from scratch for each new set of projections, we instead propose to leverage anatomical consistencies over different scans by training a single conditional NF on a dataset of projections. We propose a novel conditioning method where local modulations are modeled per patient as a field over the input domain through a Neural Modulation Field (NMF). The resulting Conditional Cone Beam Neural Tomography (CondCBNT) shows improved performance for both high and low numbers of available projections on noise-free and noisy data.

Modelling Long Range Dependencies in N-D: From Task-Specific to a General Purpose CNN

Performant Convolutional Neural Network (CNN) architectures must be tailored to specific tasks in order to consider the length, resolution, and dimensionality of the input data. In this work, we tackle the need for problem-specific CNN architectures. We present the Continuous Convolutional Neural Network (CCNN): a single CNN able to process data of arbitrary resolution, dimensionality and length without any structural changes. Its key component are its continuous convolutional kernels which model long-range dependencies at every layer, and thus remove the need of current CNN architectures for task-dependent downsampling and depths. We showcase the generality of our method by using the same architecture for tasks on sequential ($1{\rm D}$), visual ($2{\rm D}$) and point-cloud ($3{\rm D}$) data. Our CCNN matches and often outperforms the current state-of-the-art across all tasks considered.

Towards a General Purpose CNN for Long Range Dependencies in $\mathrm{N}$D

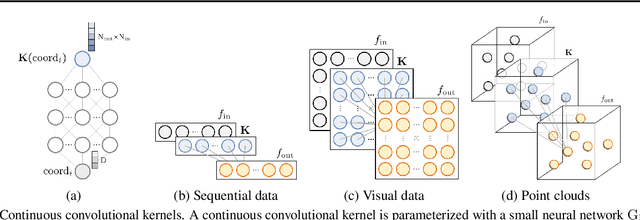
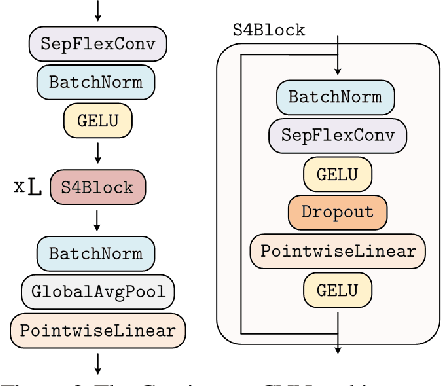
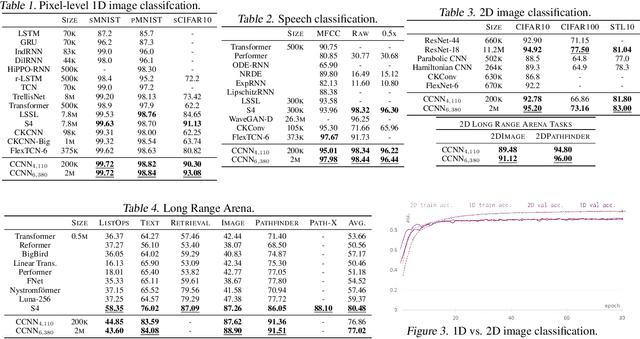
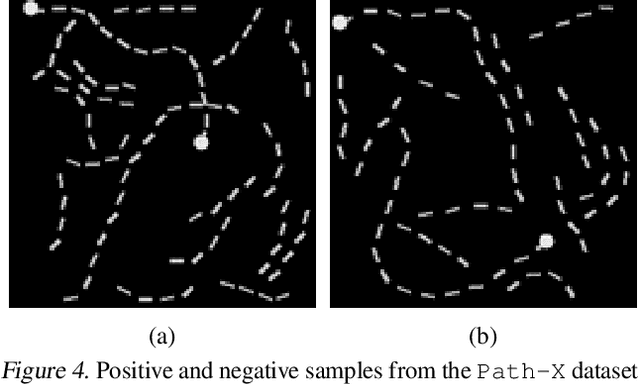
The use of Convolutional Neural Networks (CNNs) is widespread in Deep Learning due to a range of desirable model properties which result in an efficient and effective machine learning framework. However, performant CNN architectures must be tailored to specific tasks in order to incorporate considerations such as the input length, resolution, and dimentionality. In this work, we overcome the need for problem-specific CNN architectures with our Continuous Convolutional Neural Network (CCNN): a single CNN architecture equipped with continuous convolutional kernels that can be used for tasks on data of arbitrary resolution, dimensionality and length without structural changes. Continuous convolutional kernels model long range dependencies at every layer, and remove the need for downsampling layers and task-dependent depths needed in current CNN architectures. We show the generality of our approach by applying the same CCNN to a wide set of tasks on sequential (1$\mathrm{D}$) and visual data (2$\mathrm{D}$). Our CCNN performs competitively and often outperforms the current state-of-the-art across all tasks considered.

Exploiting Redundancy: Separable Group Convolutional Networks on Lie Groups

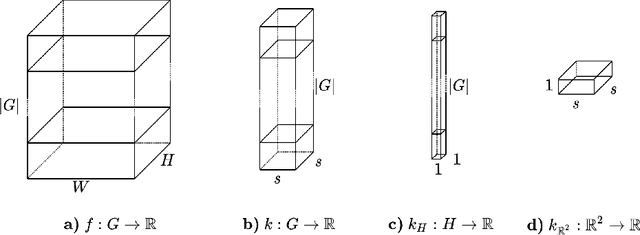
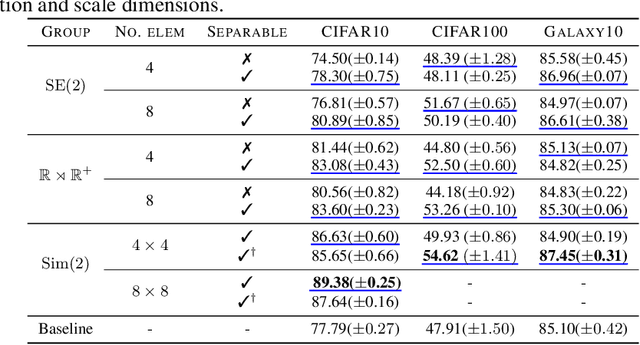
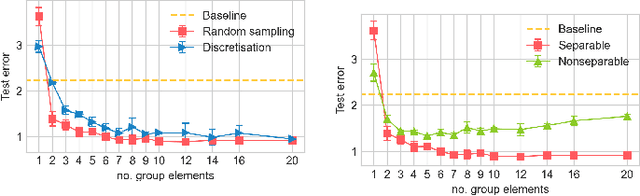
Group convolutional neural networks (G-CNNs) have been shown to increase parameter efficiency and model accuracy by incorporating geometric inductive biases. In this work, we investigate the properties of representations learned by regular G-CNNs, and show considerable parameter redundancy in group convolution kernels. This finding motivates further weight-tying by sharing convolution kernels over subgroups. To this end, we introduce convolution kernels that are separable over the subgroup and channel dimensions. In order to obtain equivariance to arbitrary affine Lie groups we provide a continuous parameterisation of separable convolution kernels. We evaluate our approach across several vision datasets, and show that our weight sharing leads to improved performance and computational efficiency. In many settings, separable G-CNNs outperform their non-separable counterpart, while only using a fraction of their training time. In addition, thanks to the increase in computational efficiency, we are able to implement G-CNNs equivariant to the $\mathrm{Sim(2)}$ group; the group of dilations, rotations and translations. $\mathrm{Sim(2)}$-equivariance further improves performance on all tasks considered.