Robust Mixture Learning when Outliers Overwhelm Small Groups

We study the problem of estimating the means of well-separated mixtures when an adversary may add arbitrary outliers. While strong guarantees are available when the outlier fraction is significantly smaller than the minimum mixing weight, much less is known when outliers may crowd out low-weight clusters - a setting we refer to as list-decodable mixture learning (LD-ML). In this case, adversarial outliers can simulate additional spurious mixture components. Hence, if all means of the mixture must be recovered up to a small error in the output list, the list size needs to be larger than the number of (true) components. We propose an algorithm that obtains order-optimal error guarantees for each mixture mean with a minimal list-size overhead, significantly improving upon list-decodable mean estimation, the only existing method that is applicable for LD-ML. Although improvements are observed even when the mixture is non-separated, our algorithm achieves particularly strong guarantees when the mixture is separated: it can leverage the mixture structure to partially cluster the samples before carefully iterating a base learner for list-decodable mean estimation at different scales.

On the Growth of Mistakes in Differentially Private Online Learning: A Lower Bound Perspective

In this paper, we provide lower bounds for Differentially Private (DP) Online Learning algorithms. Our result shows that, for a broad class of $(\varepsilon,\delta)$-DP online algorithms, for $T$ such that $\log T\leq O(1 / \delta)$, the expected number of mistakes incurred by the algorithm grows as $\Omega(\log \frac{T}{\delta})$. This matches the upper bound obtained by Golowich and Livni (2021) and is in contrast to non-private online learning where the number of mistakes is independent of $T$. To the best of our knowledge, our work is the first result towards settling lower bounds for DP-Online learning and partially addresses the open question in Sanyal and Ramponi (2022).

Asymptotics of Learning with Deep Structured (Random) Features

For a large class of feature maps we provide a tight asymptotic characterisation of the test error associated with learning the readout layer, in the high-dimensional limit where the input dimension, hidden layer widths, and number of training samples are proportionally large. This characterization is formulated in terms of the population covariance of the features. Our work is partially motivated by the problem of learning with Gaussian rainbow neural networks, namely deep non-linear fully-connected networks with random but structured weights, whose row-wise covariances are further allowed to depend on the weights of previous layers. For such networks we also derive a closed-form formula for the feature covariance in terms of the weight matrices. We further find that in some cases our results can capture feature maps learned by deep, finite-width neural networks trained under gradient descent.

Deterministic equivalent and error universality of deep random features learning

This manuscript considers the problem of learning a random Gaussian network function using a fully connected network with frozen intermediate layers and trainable readout layer. This problem can be seen as a natural generalization of the widely studied random features model to deeper architectures. First, we prove Gaussian universality of the test error in a ridge regression setting where the learner and target networks share the same intermediate layers, and provide a sharp asymptotic formula for it. Establishing this result requires proving a deterministic equivalent for traces of the deep random features sample covariance matrices which can be of independent interest. Second, we conjecture the asymptotic Gaussian universality of the test error in the more general setting of arbitrary convex losses and generic learner/target architectures. We provide extensive numerical evidence for this conjecture, which requires the derivation of closed-form expressions for the layer-wise post-activation population covariances. In light of our results, we investigate the interplay between architecture design and implicit regularization.

Dynamic Model Pruning with Feedback

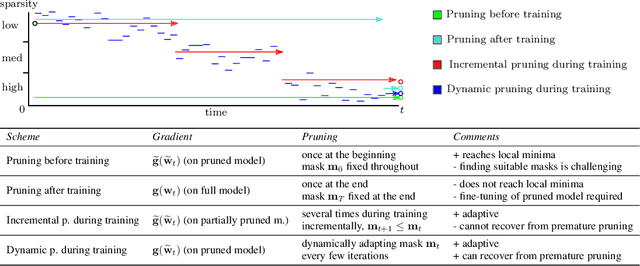
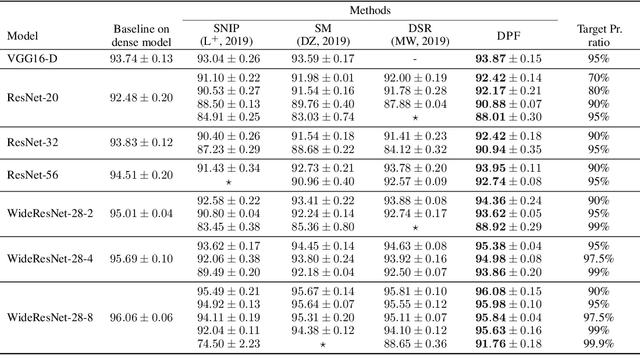
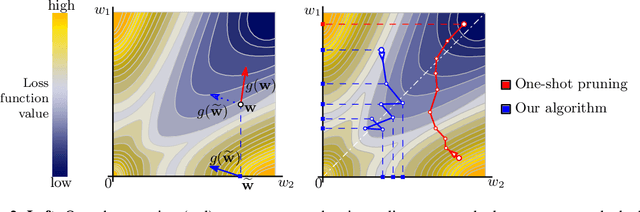
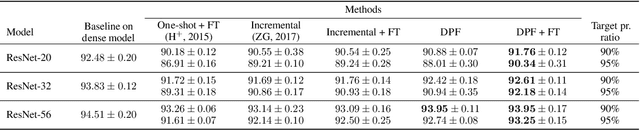
Deep neural networks often have millions of parameters. This can hinder their deployment to low-end devices, not only due to high memory requirements but also because of increased latency at inference. We propose a novel model compression method that generates a sparse trained model without additional overhead: by allowing (i) dynamic allocation of the sparsity pattern and (ii) incorporating feedback signal to reactivate prematurely pruned weights we obtain a performant sparse model in one single training pass (retraining is not needed, but can further improve the performance). We evaluate our method on CIFAR-10 and ImageNet, and show that the obtained sparse models can reach the state-of-the-art performance of dense models. Moreover, their performance surpasses that of models generated by all previously proposed pruning schemes.