Dataset-Adaptive Dimensionality Reduction

Selecting the appropriate dimensionality reduction (DR) technique and determining its optimal hyperparameter settings that maximize the accuracy of the output projections typically involves extensive trial and error, often resulting in unnecessary computational overhead. To address this challenge, we propose a dataset-adaptive approach to DR optimization guided by structural complexity metrics. These metrics quantify the intrinsic complexity of a dataset, predicting whether higher-dimensional spaces are necessary to represent it accurately. Since complex datasets are often inaccurately represented in two-dimensional projections, leveraging these metrics enables us to predict the maximum achievable accuracy of DR techniques for a given dataset, eliminating redundant trials in optimizing DR. We introduce the design and theoretical foundations of these structural complexity metrics. We quantitatively verify that our metrics effectively approximate the ground truth complexity of datasets and confirm their suitability for guiding dataset-adaptive DR workflow. Finally, we empirically show that our dataset-adaptive workflow significantly enhances the efficiency of DR optimization without compromising accuracy.

Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

Bayesian Optimization over Permutation Spaces

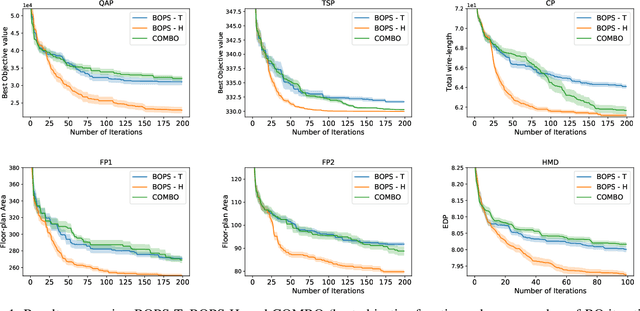
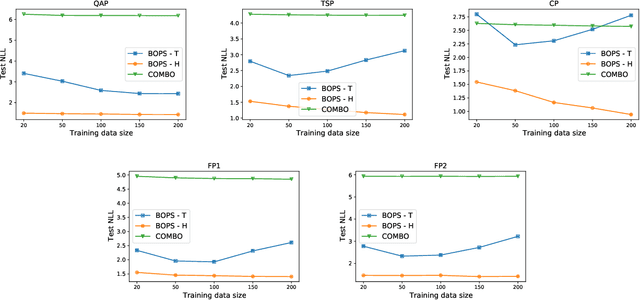
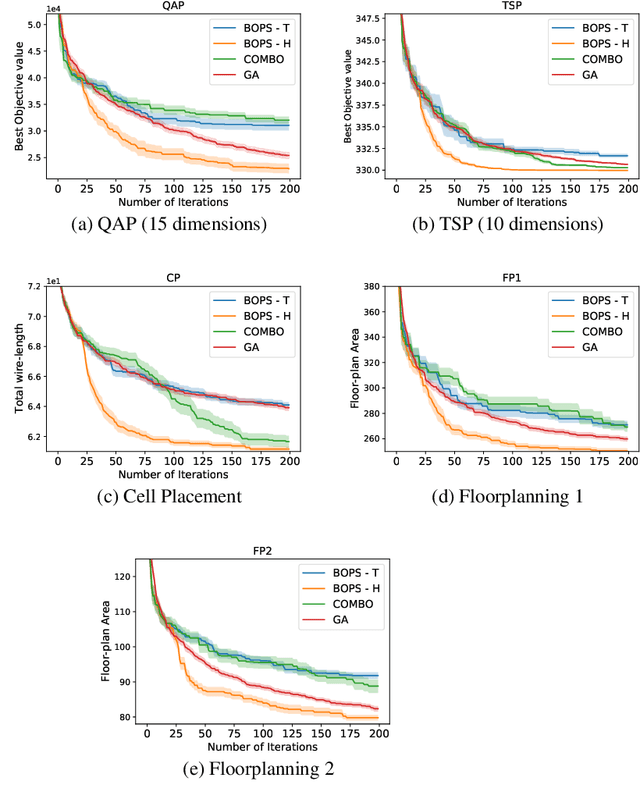
Optimizing expensive to evaluate black-box functions over an input space consisting of all permutations of d objects is an important problem with many real-world applications. For example, placement of functional blocks in hardware design to optimize performance via simulations. The overall goal is to minimize the number of function evaluations to find high-performing permutations. The key challenge in solving this problem using the Bayesian optimization (BO) framework is to trade-off the complexity of statistical model and tractability of acquisition function optimization. In this paper, we propose and evaluate two algorithms for BO over Permutation Spaces (BOPS). First, BOPS-T employs Gaussian process (GP) surrogate model with Kendall kernels and a Tractable acquisition function optimization approach based on Thompson sampling to select the sequence of permutations for evaluation. Second, BOPS-H employs GP surrogate model with Mallow kernels and a Heuristic search approach to optimize expected improvement acquisition function. We theoretically analyze the performance of BOPS-T to show that their regret grows sub-linearly. Our experiments on multiple synthetic and real-world benchmarks show that both BOPS-T and BOPS-H perform better than the state-of-the-art BO algorithm for combinatorial spaces. To drive future research on this important problem, we make new resources and real-world benchmarks available to the community.