Privacy-Preserving Conformal Prediction Under Local Differential Privacy

Conformal prediction (CP) provides sets of candidate classes with a guaranteed probability of containing the true class. However, it typically relies on a calibration set with clean labels. We address privacy-sensitive scenarios where the aggregator is untrusted and can only access a perturbed version of the true labels. We propose two complementary approaches under local differential privacy (LDP). In the first approach, users do not access the model but instead provide their input features and a perturbed label using a k-ary randomized response. In the second approach, which enforces stricter privacy constraints, users add noise to their conformity score by binary search response. This method requires access to the classification model but preserves both data and label privacy. Both approaches compute the conformal threshold directly from noisy data without accessing the true labels. We prove finite-sample coverage guarantees and demonstrate robust coverage even under severe randomization. This approach unifies strong local privacy with predictive uncertainty control, making it well-suited for sensitive applications such as medical imaging or large language model queries, regardless of whether users can (or are willing to) compute their own scores.

Calibration of Network Confidence for Unsupervised Domain Adaptation Using Estimated Accuracy

This study addresses the problem of calibrating network confidence while adapting a model that was originally trained on a source domain to a target domain using unlabeled samples from the target domain. The absence of labels from the target domain makes it impossible to directly calibrate the adapted network on the target domain. To tackle this challenge, we introduce a calibration procedure that relies on estimating the network's accuracy on the target domain. The network accuracy is first computed on the labeled source data and then is modified to represent the actual accuracy of the model on the target domain. The proposed algorithm calibrates the prediction confidence directly in the target domain by minimizing the disparity between the estimated accuracy and the computed confidence. The experimental results show that our method significantly outperforms existing methods, which rely on importance weighting, across several standard datasets.

A Conformal Prediction Score that is Robust to Label Noise

Conformal Prediction (CP) quantifies network uncertainty by building a small prediction set with a pre-defined probability that the correct class is within this set. In this study we tackle the problem of CP calibration based on a validation set with noisy labels. We introduce a conformal score that is robust to label noise. The noise-free conformal score is estimated using the noisy labeled data and the noise level. In the test phase the noise-free score is used to form the prediction set. We applied the proposed algorithm to several standard medical imaging classification datasets. We show that our method outperforms current methods by a large margin, in terms of the average size of the prediction set, while maintaining the required coverage.

A Study on the Evaluation of Generative Models

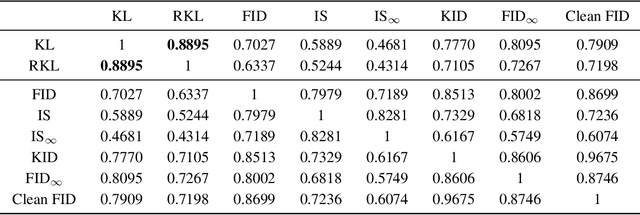
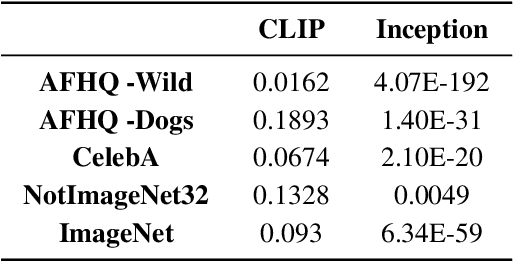
Implicit generative models, which do not return likelihood values, such as generative adversarial networks and diffusion models, have become prevalent in recent years. While it is true that these models have shown remarkable results, evaluating their performance is challenging. This issue is of vital importance to push research forward and identify meaningful gains from random noise. Currently, heuristic metrics such as the Inception score (IS) and Frechet Inception Distance (FID) are the most common evaluation metrics, but what they measure is not entirely clear. Additionally, there are questions regarding how meaningful their score actually is. In this work, we study the evaluation metrics of generative models by generating a high-quality synthetic dataset on which we can estimate classical metrics for comparison. Our study shows that while FID and IS do correlate to several f-divergences, their ranking of close models can vary considerably making them problematic when used for fain-grained comparison. We further used this experimental setting to study which evaluation metric best correlates with our probabilistic metrics. Lastly, we look into the base features used for metrics such as FID.

Functional Ensemble Distillation

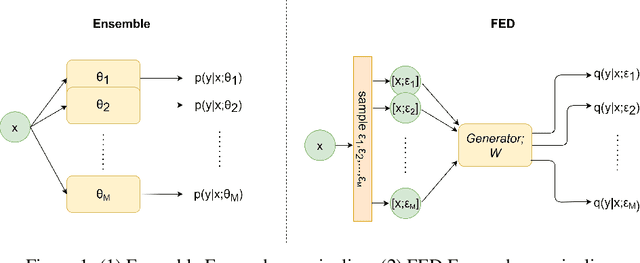
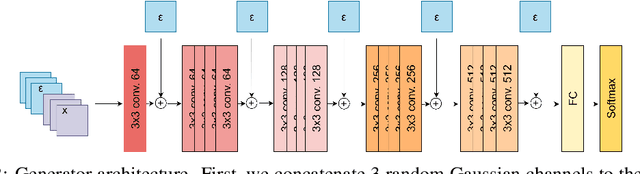
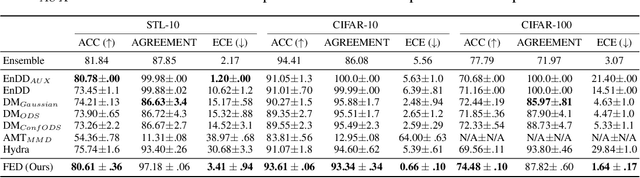
Bayesian models have many desirable properties, most notable is their ability to generalize from limited data and to properly estimate the uncertainty in their predictions. However, these benefits come at a steep computational cost as Bayesian inference, in most cases, is computationally intractable. One popular approach to alleviate this problem is using a Monte-Carlo estimation with an ensemble of models sampled from the posterior. However, this approach still comes at a significant computational cost, as one needs to store and run multiple models at test time. In this work, we investigate how to best distill an ensemble's predictions using an efficient model. First, we argue that current approaches that simply return distribution over predictions cannot compute important properties, such as the covariance between predictions, which can be valuable for further processing. Second, in many limited data settings, all ensemble members achieve nearly zero training loss, namely, they produce near-identical predictions on the training set which results in sub-optimal distilled models. To address both problems, we propose a novel and general distillation approach, named Functional Ensemble Distillation (FED), and we investigate how to best distill an ensemble in this setting. We find that learning the distilled model via a simple augmentation scheme in the form of mixup augmentation significantly boosts the performance. We evaluated our method on several tasks and showed that it achieves superior results in both accuracy and uncertainty estimation compared to current approaches.