Deep Archimedean Copulas

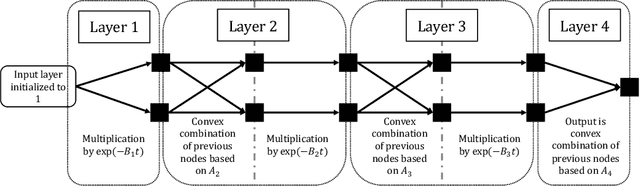
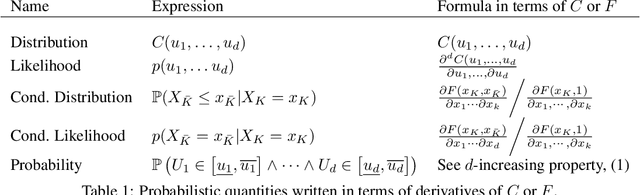
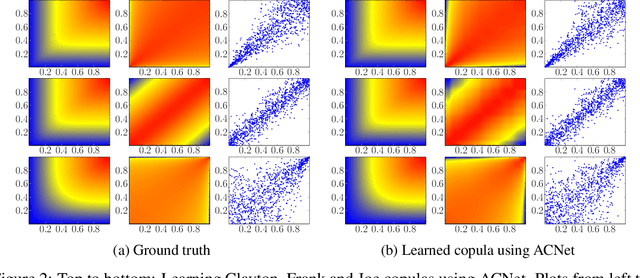
A central problem in machine learning and statistics is to model joint densities of random variables from data. Copulas are joint cumulative distribution functions with uniform marginal distributions and are used to capture interdependencies in isolation from marginals. Copulas are widely used within statistics, but have not gained traction in the context of modern deep learning. In this paper, we introduce ACNet, a novel differentiable neural network architecture that enforces structural properties and enables one to learn an important class of copulas--Archimedean Copulas. Unlike Generative Adversarial Networks, Variational Autoencoders, or Normalizing Flow methods, which learn either densities or the generative process directly, ACNet learns a generator of the copula, which implicitly defines the cumulative distribution function of a joint distribution. We give a probabilistic interpretation of the network parameters of ACNet and use this to derive a simple but efficient sampling algorithm for the learned copula. Our experiments show that ACNet is able to both approximate common Archimedean Copulas and generate new copulas which may provide better fits to data.

Nonmyopic Gaussian Process Optimization with Macro-Actions

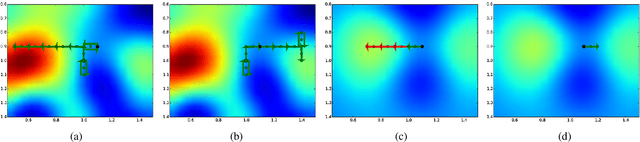
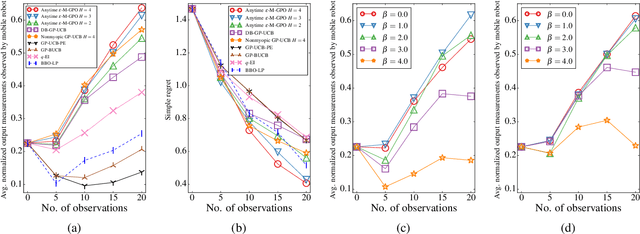
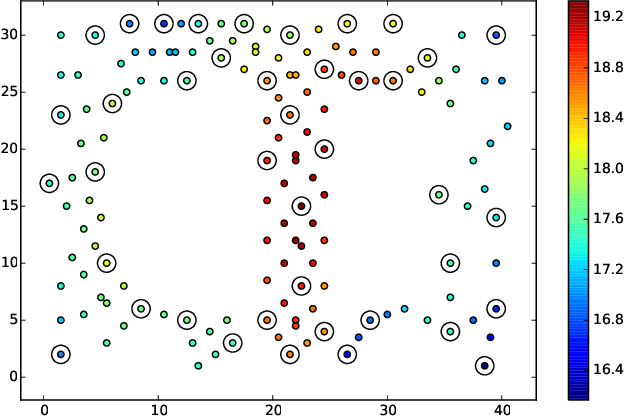
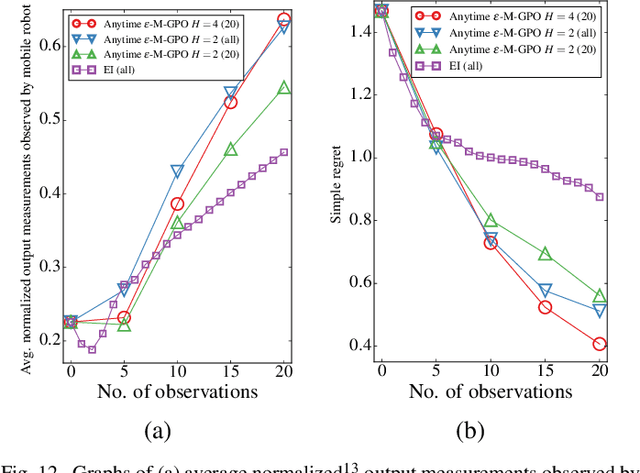
This paper presents a multi-staged approach to nonmyopic adaptive Gaussian process optimization (GPO) for Bayesian optimization (BO) of unknown, highly complex objective functions that, in contrast to existing nonmyopic adaptive BO algorithms, exploits the notion of macro-actions for scaling up to a further lookahead to match up to a larger available budget. To achieve this, we generalize GP upper confidence bound to a new acquisition function defined w.r.t. a nonmyopic adaptive macro-action policy, which is intractable to be optimized exactly due to an uncountable set of candidate outputs. The contribution of our work here is thus to derive a nonmyopic adaptive epsilon-Bayes-optimal macro-action GPO (epsilon-Macro-GPO) policy. To perform nonmyopic adaptive BO in real time, we then propose an asymptotically optimal anytime variant of our epsilon-Macro-GPO policy with a performance guarantee. We empirically evaluate the performance of our epsilon-Macro-GPO policy and its anytime variant in BO with synthetic and real-world datasets.

Efficient Regret Minimization Algorithm for Extensive-Form Correlated Equilibrium

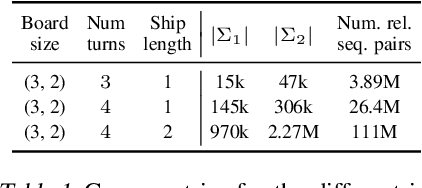
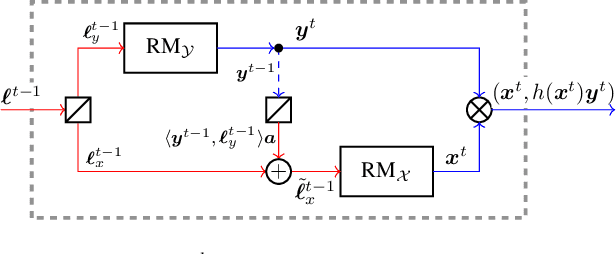
Self-play methods based on regret minimization have become the state of the art for computing Nash equilibria in large two-players zero-sum extensive-form games. These methods fundamentally rely on the hierarchical structure of the players' sequential strategy spaces to construct a regret minimizer that recursively minimizes regret at each decision point in the game tree. In this paper, we introduce the first efficient regret minimization algorithm for computing extensive-form correlated equilibria in large two-player general-sum games with no chance moves. Designing such an algorithm is significantly more challenging than designing one for the Nash equilibrium counterpart, as the constraints that define the space of correlation plans lack the hierarchical structure and might even form cycles. We show that some of the constraints are redundant and can be excluded from consideration, and present an efficient algorithm that generates the space of extensive-form correlation plans incrementally from the remaining constraints. This structural decomposition is achieved via a special convexity-preserving operation that we coin scaled extension. We show that a regret minimizer can be designed for a scaled extension of any two convex sets, and that from the decomposition we then obtain a global regret minimizer. Our algorithm produces feasible iterates. Experiments show that it significantly outperforms prior approaches and for larger problems it is the only viable option.

Large Scale Learning of Agent Rationality in Two-Player Zero-Sum Games

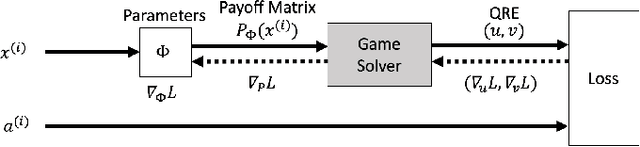
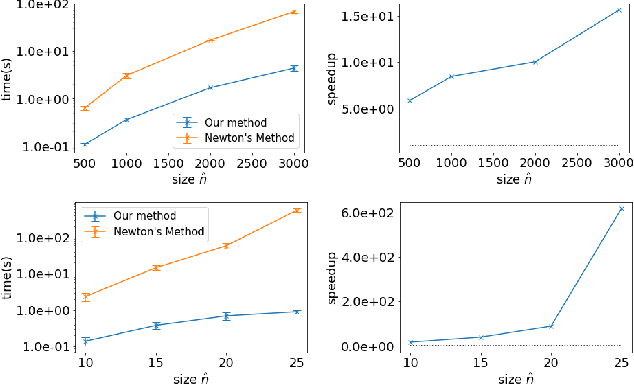
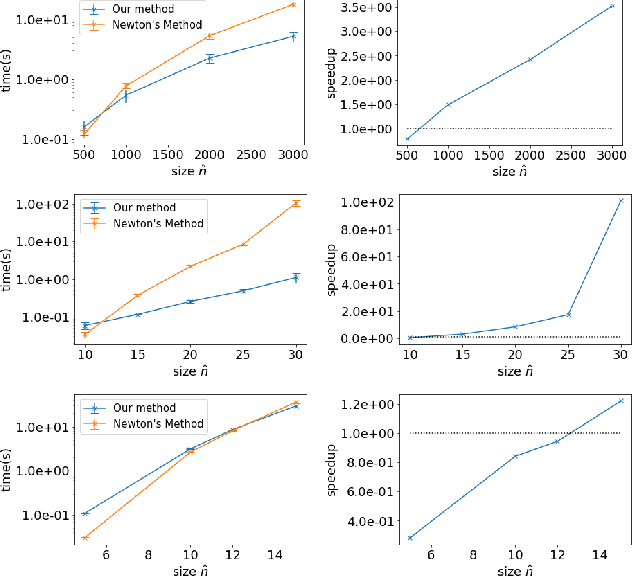
With the recent advances in solving large, zero-sum extensive form games, there is a growing interest in the inverse problem of inferring underlying game parameters given only access to agent actions. Although a recent work provides a powerful differentiable end-to-end learning frameworks which embed a game solver within a deep-learning framework, allowing unknown game parameters to be learned via backpropagation, this framework faces significant limitations when applied to boundedly rational human agents and large scale problems, leading to poor practicality. In this paper, we address these limitations and propose a framework that is applicable for more practical settings. First, seeking to learn the rationality of human agents in complex two-player zero-sum games, we draw upon well-known ideas in decision theory to obtain a concise and interpretable agent behavior model, and derive solvers and gradients for end-to-end learning. Second, to scale up to large, real-world scenarios, we propose an efficient first-order primal-dual method which exploits the structure of extensive-form games, yielding significantly faster computation for both game solving and gradient computation. When tested on randomly generated games, we report speedups of orders of magnitude over previous approaches. We also demonstrate the effectiveness of our model on both real-world one-player settings and synthetic data.

What game are we playing? End-to-end learning in normal and extensive form games

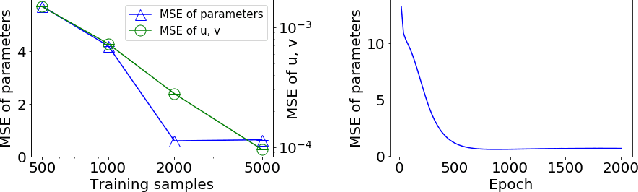
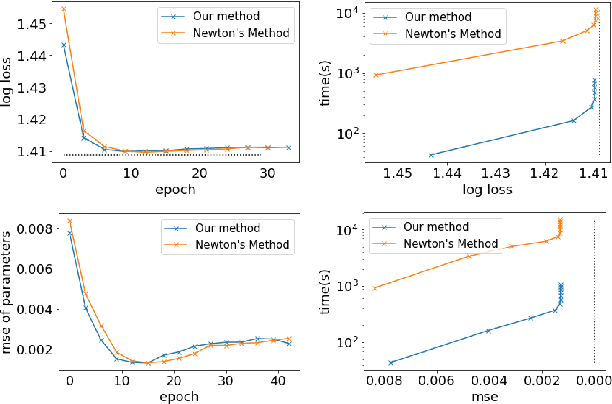
Although recent work in AI has made great progress in solving large, zero-sum, extensive-form games, the underlying assumption in most past work is that the parameters of the game itself are known to the agents. This paper deals with the relatively under-explored but equally important "inverse" setting, where the parameters of the underlying game are not known to all agents, but must be learned through observations. We propose a differentiable, end-to-end learning framework for addressing this task. In particular, we consider a regularized version of the game, equivalent to a particular form of quantal response equilibrium, and develop 1) a primal-dual Newton method for finding such equilibrium points in both normal and extensive form games; and 2) a backpropagation method that lets us analytically compute gradients of all relevant game parameters through the solution itself. This ultimately lets us learn the game by training in an end-to-end fashion, effectively by integrating a "differentiable game solver" into the loop of larger deep network architectures. We demonstrate the effectiveness of the learning method in several settings including poker and security game tasks.

Gaussian Process Planning with Lipschitz Continuous Reward Functions: Towards Unifying Bayesian Optimization, Active Learning, and Beyond

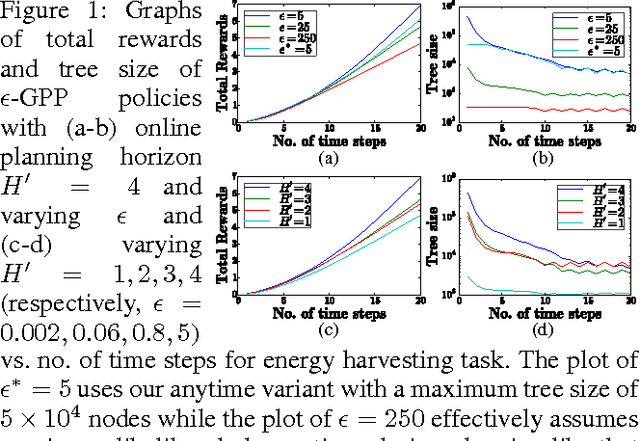
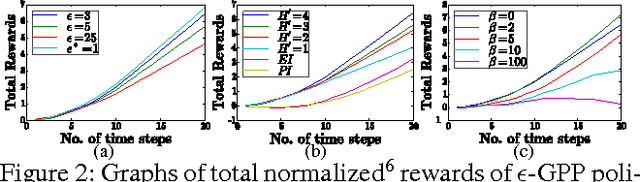
This paper presents a novel nonmyopic adaptive Gaussian process planning (GPP) framework endowed with a general class of Lipschitz continuous reward functions that can unify some active learning/sensing and Bayesian optimization criteria and offer practitioners some flexibility to specify their desired choices for defining new tasks/problems. In particular, it utilizes a principled Bayesian sequential decision problem framework for jointly and naturally optimizing the exploration-exploitation trade-off. In general, the resulting induced GPP policy cannot be derived exactly due to an uncountable set of candidate observations. A key contribution of our work here thus lies in exploiting the Lipschitz continuity of the reward functions to solve for a nonmyopic adaptive epsilon-optimal GPP (epsilon-GPP) policy. To plan in real time, we further propose an asymptotically optimal, branch-and-bound anytime variant of epsilon-GPP with performance guarantee. We empirically demonstrate the effectiveness of our epsilon-GPP policy and its anytime variant in Bayesian optimization and an energy harvesting task.