Chuan-Shen Hu
A Sheaf-Theoretic and Topological Perspective on Complex Network Modeling and Attention Mechanisms in Graph Neural Models
Jan 29, 2026Abstract:Combinatorial and topological structures, such as graphs, simplicial complexes, and cell complexes, form the foundation of geometric and topological deep learning (GDL and TDL) architectures. These models aggregate signals over such domains, integrate local features, and generate representations for diverse real-world applications. However, the distribution and diffusion behavior of GDL and TDL features during training remains an open and underexplored problem. Motivated by this gap, we introduce a cellular sheaf theoretic framework for modeling and analyzing the local consistency and harmonicity of node features and edge weights in graph-based architectures. By tracking local feature alignments and agreements through sheaf structures, the framework offers a topological perspective on feature diffusion and aggregation. Furthermore, a multiscale extension inspired by topological data analysis (TDA) is proposed to capture hierarchical feature interactions in graph models. This approach enables a joint characterization of GDL and TDL architectures based on their underlying geometric and topological structures and the learned signals defined on them, providing insights for future studies on conventional tasks such as node classification, substructure detection, and community detection.
Quotient Complex Transformer (QCformer) for Perovskite Data Analysis
May 14, 2025Abstract:The discovery of novel functional materials is crucial in addressing the challenges of sustainable energy generation and climate change. Hybrid organic-inorganic perovskites (HOIPs) have gained attention for their exceptional optoelectronic properties in photovoltaics. Recently, geometric deep learning, particularly graph neural networks (GNNs), has shown strong potential in predicting material properties and guiding material design. However, traditional GNNs often struggle to capture the periodic structures and higher-order interactions prevalent in such systems. To address these limitations, we propose a novel representation based on quotient complexes (QCs) and introduce the Quotient Complex Transformer (QCformer) for material property prediction. A material structure is modeled as a quotient complex, which encodes both pairwise and many-body interactions via simplices of varying dimensions and captures material periodicity through a quotient operation. Our model leverages higher-order features defined on simplices and processes them using a simplex-based Transformer module. We pretrain QCformer on benchmark datasets such as the Materials Project and JARVIS, and fine-tune it on HOIP datasets. The results show that QCformer outperforms state-of-the-art models in HOIP property prediction, demonstrating its effectiveness. The quotient complex representation and QCformer model together contribute a powerful new tool for predictive modeling of perovskite materials.
A Multi-parameter Persistence Framework for Mathematical Morphology
Mar 24, 2021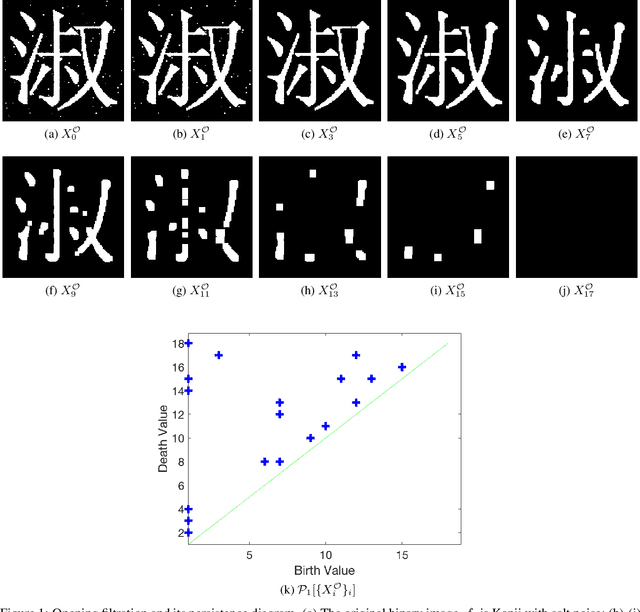
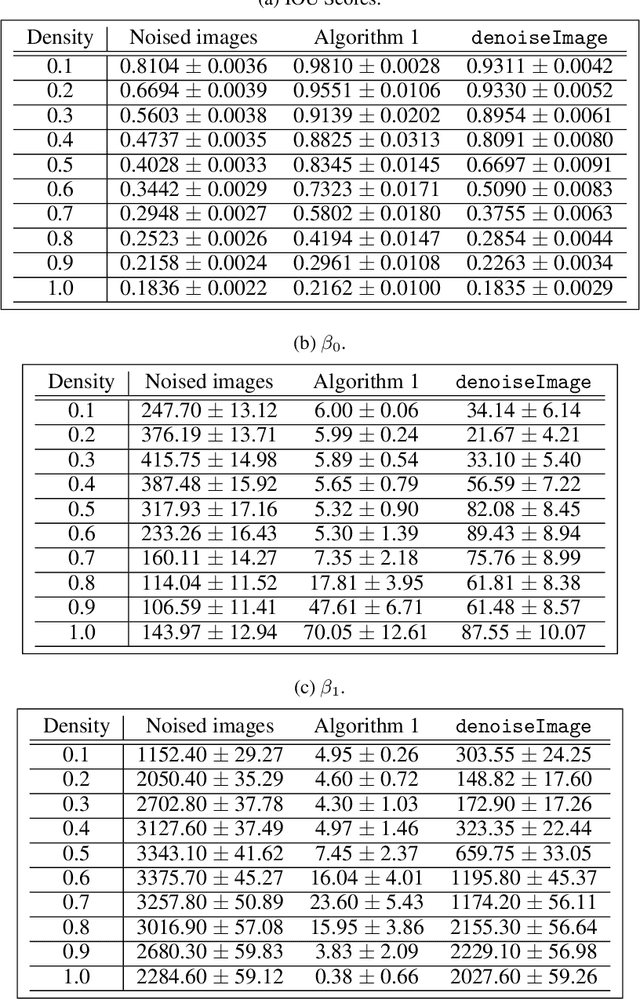

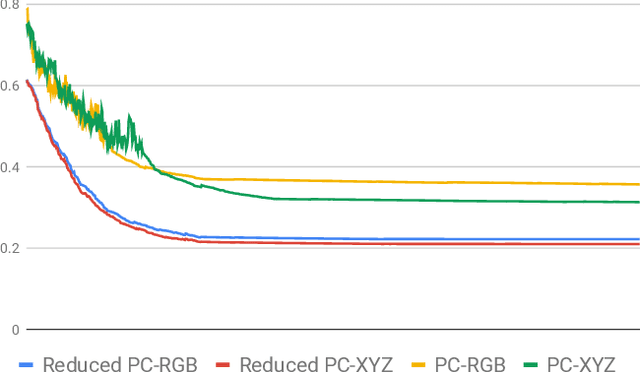
Abstract:The field of mathematical morphology offers well-studied techniques for image processing. In this work, we view morphological operations through the lens of persistent homology, a tool at the heart of the field of topological data analysis. We demonstrate that morphological operations naturally form a multiparameter filtration and that persistent homology can then be used to extract information about both topology and geometry in the images as well as to automate methods for optimizing the study and rendering of structure in images. For illustration, we apply this framework to analyze noisy binary, grayscale, and color images.
A Sheaf and Topology Approach to Generating Local Branch Numbers in Digital Images
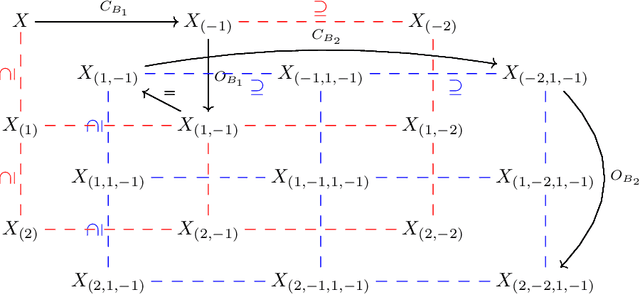
Dec 03, 2020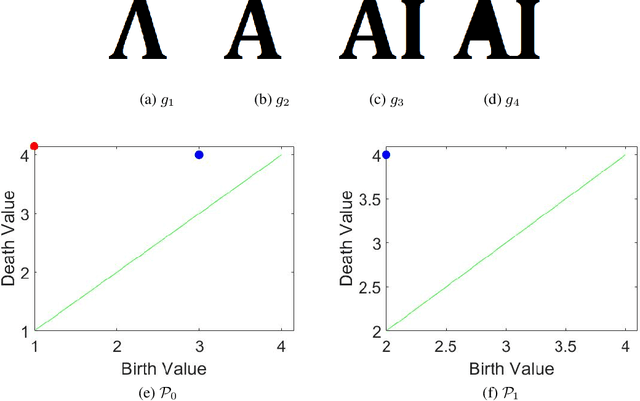
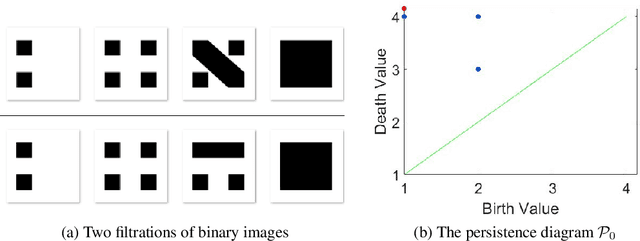
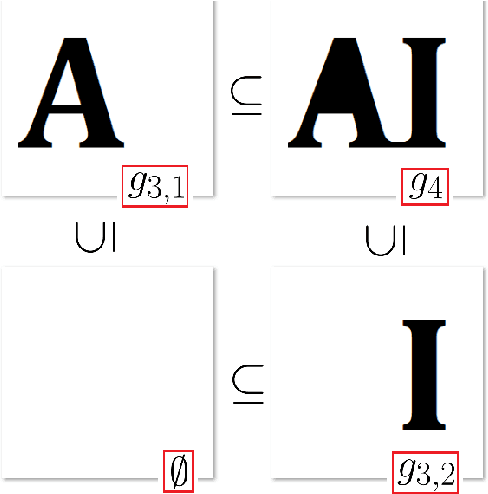

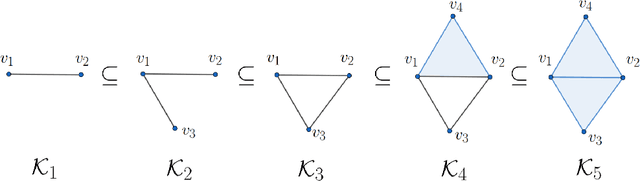
Abstract:This paper concerns a theoretical approach that combines topological data analysis (TDA) and sheaf theory. Topological data analysis, a rising field in mathematics and computer science, concerns the shape of the data and has been proven effective in many scientific disciplines. Sheaf theory, a mathematics subject in algebraic geometry, provides a framework for describing the local consistency in geometric objects. Persistent homology (PH) is one of the main driving forces in TDA, and the idea is to track changes of geometric objects at different scales. The persistence diagram (PD) summarizes the information of PH in the form of a multi-set. While PD provides useful information about the underlying objects, it lacks fine relations about the local consistency of specific pairs of generators in PD, such as the merging relation between two connected components in the PH. The sheaf structure provides a novel point of view for describing the merging relation of local objects in PH. It is the goal of this paper to establish a theoretic framework that utilizes the sheaf theory to uncover finer information from the PH. We also show that the proposed theory can be applied to identify the branch numbers of local objects in digital images.
A persistent homology approach to heart rate variability analysis with an application to sleep-wake classification
Aug 09, 2019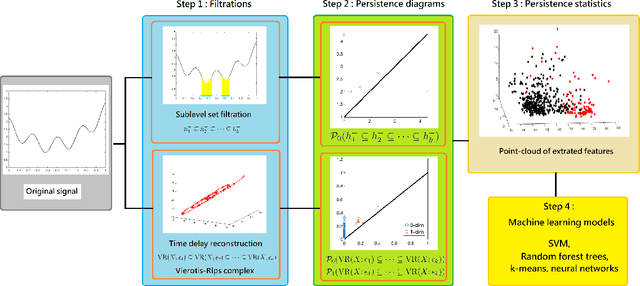
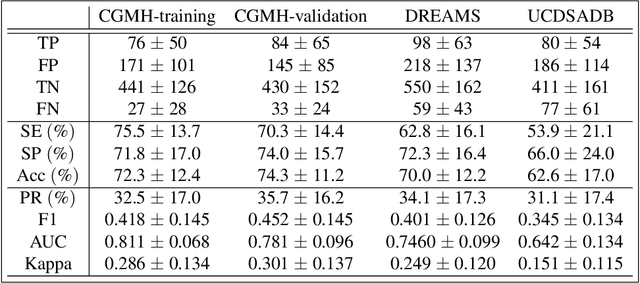
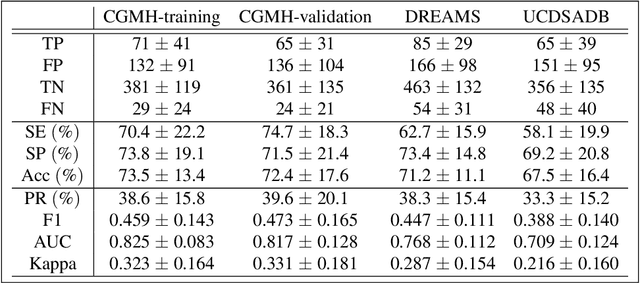
Abstract:Persistent homology (PH) is a recently developed theory in the field of algebraic topology. It is an effective and robust tool to study shapes of datasets and has been widely applied. We demonstrate a general pipeline to apply PH to study time series; particularly the heart rate variability (HRV). First, we study the shapes of time series in two different ways -- sub-level set and Taken's lag map. Second, we propose a systematic approach to summarize/vectorize persistence diagrams, a companion tool of PH. To demonstrate our proposed method, we apply these tools to the HRV analysis and the sleep-wake, REM-NREM (rapid eyeball movement and non rapid eyeball movement) and sleep-REM-NREM classification problems. The proposed algorithm is evaluated on three different datasets via the cross-database validation scheme. The performance of our approach is comparable with the state-of-the-art algorithms, and are consistent throughout these different datasets.
TopoResNet: A hybrid deep learning architecture and its application to skin lesion classification
May 13, 2019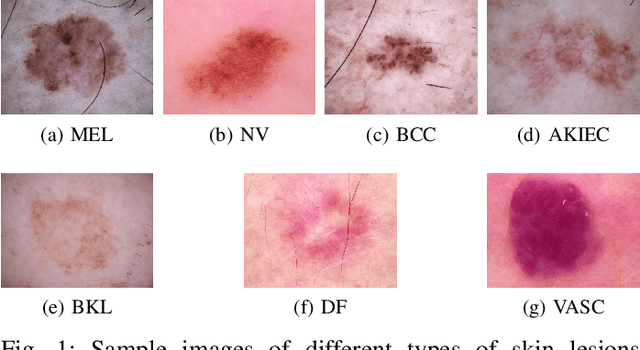
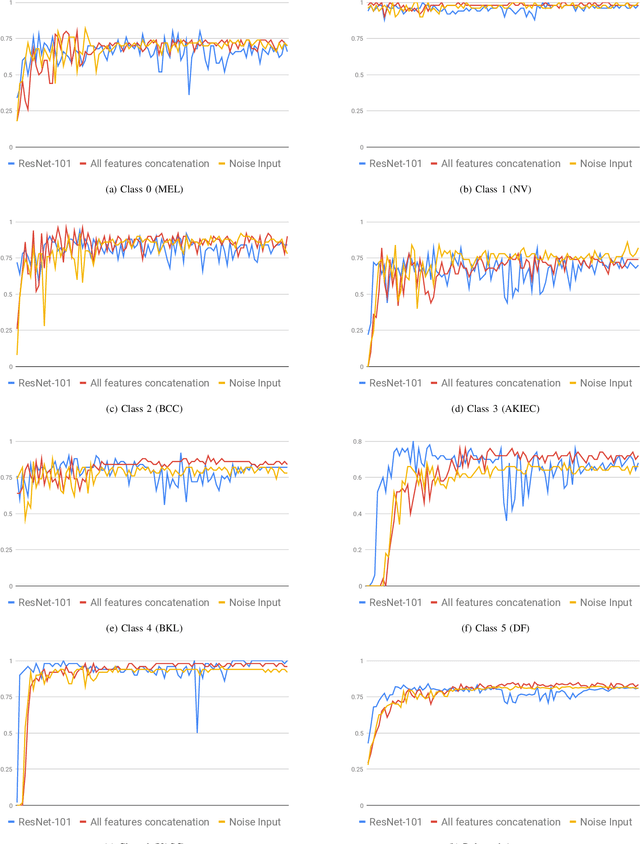
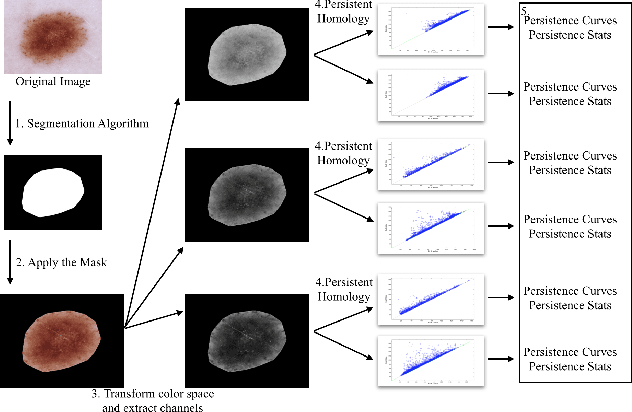
Abstract:Skin cancer is one of the most common cancers in the United States. As technological advancements are made, algorithmic diagnosis of skin lesions is becoming more important. In this paper, we develop algorithms for segmenting the actual diseased area of skin in a given image of a skin lesion, and for classifying different types of skin lesions pictured in a given image. The cores of the algorithms used were based in persistent homology, an algebraic topology technique that is part of the rising field of Topological Data Analysis (TDA). The segmentation algorithm utilizes a similar concept to persistent homology that captures the robustness of segmented regions. For classification, we design two families of topological features from persistence diagrams---which we refer to as {\em persistence statistics} (PS) and {\em persistence curves} (PC), and use linear support vector machine as classifiers. We also combined those topological features, PS and PC, into ResNet-101 model, which we call {\em TopoResNet-101}, the results show that PS and PC are effective in two folds---improving classification performances and stabilizing the training process. Although convolutional features are the most important learning targets in CNN models, global information of images may be lost in the training process. Because topological features were extracted globally, our results show that the global property of topological features provide additional information to machine learning models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge