Classification of Firn Data via Topological Features

In this paper we evaluate the performance of topological features for generalizable and robust classification of firn image data, with the broader goal of understanding the advantages, pitfalls, and trade-offs in topological featurization. Firn refers to layers of granular snow within glaciers that haven't been compressed into ice. This compactification process imposes distinct topological and geometric structure on firn that varies with depth within the firn column, making topological data analysis (TDA) a natural choice for understanding the connection between depth and structure. We use two classes of topological features, sublevel set features and distance transform features, together with persistence curves, to predict sample depth from microCT images. A range of challenging training-test scenarios reveals that no one choice of method dominates in all categories, and uncoveres a web of trade-offs between accuracy, interpretability, and generalizability.

A Multi-parameter Persistence Framework for Mathematical Morphology

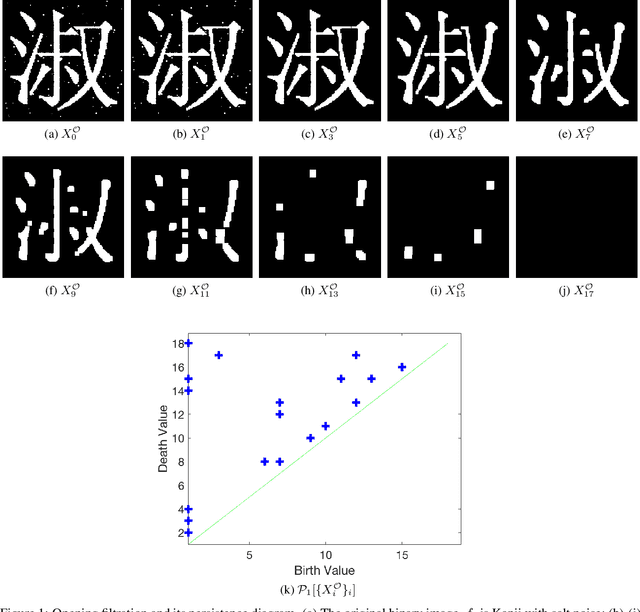
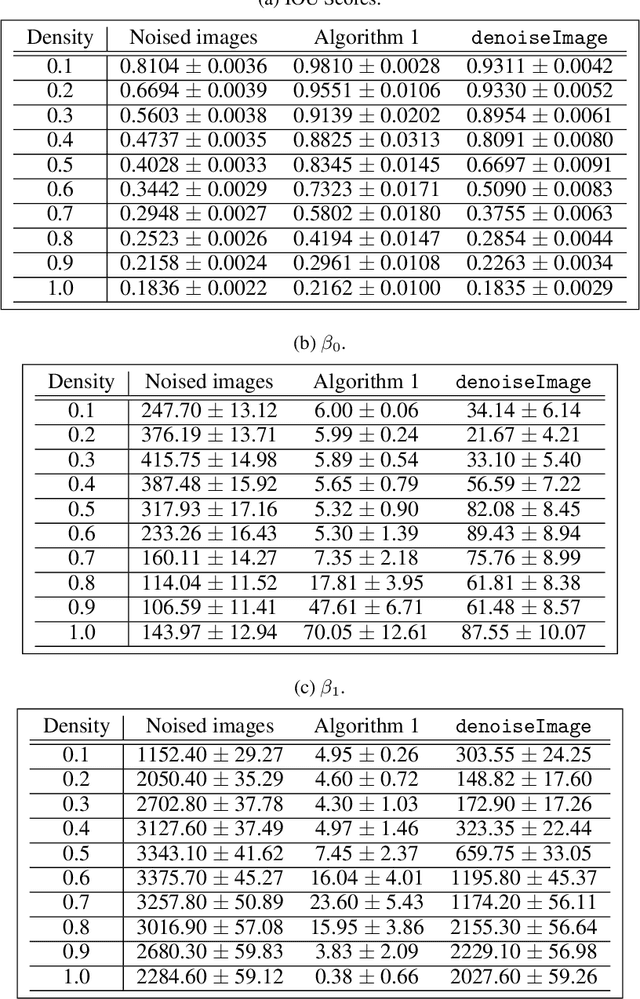
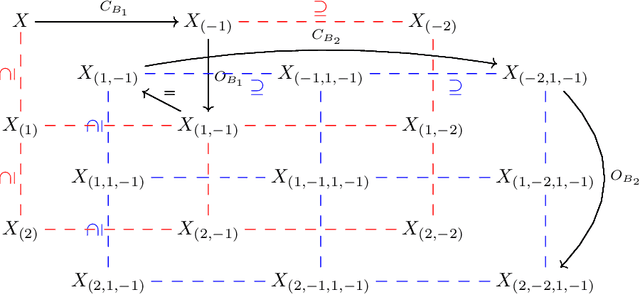
The field of mathematical morphology offers well-studied techniques for image processing. In this work, we view morphological operations through the lens of persistent homology, a tool at the heart of the field of topological data analysis. We demonstrate that morphological operations naturally form a multiparameter filtration and that persistent homology can then be used to extract information about both topology and geometry in the images as well as to automate methods for optimizing the study and rendering of structure in images. For illustration, we apply this framework to analyze noisy binary, grayscale, and color images.