Christopher M. Bishop
A Scientific Reasoning Model for Organic Synthesis Procedure Generation
Dec 15, 2025Abstract:Solving computer-aided synthesis planning is essential for enabling fully automated, robot-assisted synthesis workflows and improving the efficiency of drug discovery. A key challenge, however, is bridging the gap between computational route design and practical laboratory execution, particularly the accurate prediction of viable experimental procedures for each synthesis step. In this work, we present QFANG, a scientific reasoning language model capable of generating precise, structured experimental procedures directly from reaction equations, with explicit chain-of-thought reasoning. To develop QFANG, we curated a high-quality dataset comprising 905,990 chemical reactions paired with structured action sequences, extracted and processed from patent literature using large language models. We introduce a Chemistry-Guided Reasoning (CGR) framework that produces chain-of-thought data grounded in chemical knowledge at scale. The model subsequently undergoes supervised fine-tuning to elicit complex chemistry reasoning. Finally, we apply Reinforcement Learning from Verifiable Rewards (RLVR) to further enhance procedural accuracy. Experimental results demonstrate that QFANG outperforms advanced general-purpose reasoning models and nearest-neighbor retrieval baselines, measured by traditional NLP similarity metrics and a chemically aware evaluator using an LLM-as-a-judge. Moreover, QFANG generalizes to certain out-of-domain reaction classes and adapts to variations in laboratory conditions and user-specific constraints. We believe that QFANG's ability to generate high-quality synthesis procedures represents an important step toward bridging the gap between computational synthesis planning and fully automated laboratory synthesis.
Accurate and scalable exchange-correlation with deep learning
Jun 18, 2025Abstract:Density Functional Theory (DFT) is the most widely used electronic structure method for predicting the properties of molecules and materials. Although DFT is, in principle, an exact reformulation of the Schr\"odinger equation, practical applications rely on approximations to the unknown exchange-correlation (XC) functional. Most existing XC functionals are constructed using a limited set of increasingly complex, hand-crafted features that improve accuracy at the expense of computational efficiency. Yet, no current approximation achieves the accuracy and generality for predictive modeling of laboratory experiments at chemical accuracy -- typically defined as errors below 1 kcal/mol. In this work, we present Skala, a modern deep learning-based XC functional that bypasses expensive hand-designed features by learning representations directly from data. Skala achieves chemical accuracy for atomization energies of small molecules while retaining the computational efficiency typical of semi-local DFT. This performance is enabled by training on an unprecedented volume of high-accuracy reference data generated using computationally intensive wavefunction-based methods. Notably, Skala systematically improves with additional training data covering diverse chemistry. By incorporating a modest amount of additional high-accuracy data tailored to chemistry beyond atomization energies, Skala achieves accuracy competitive with the best-performing hybrid functionals across general main group chemistry, at the cost of semi-local DFT. As the training dataset continues to expand, Skala is poised to further enhance the predictive power of first-principles simulations.
Mixture Representations for Inference and Learning in Boltzmann Machines
Jan 30, 2013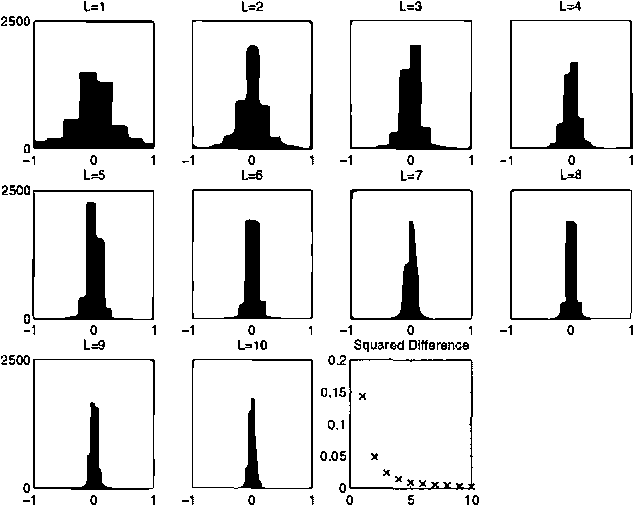
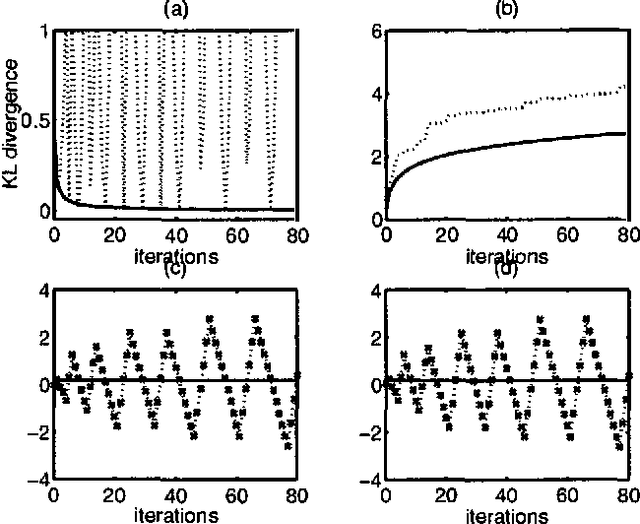
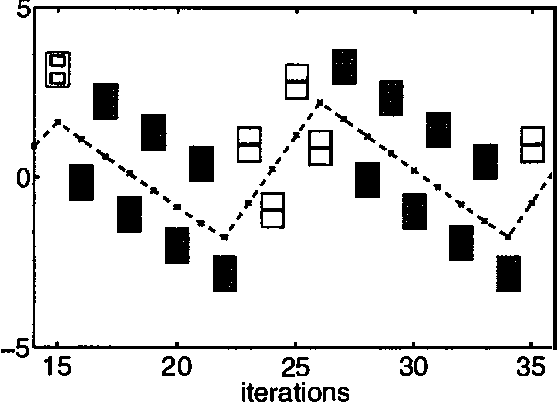
Abstract:Boltzmann machines are undirected graphical models with two-state stochastic variables, in which the logarithms of the clique potentials are quadratic functions of the node states. They have been widely studied in the neural computing literature, although their practical applicability has been limited by the difficulty of finding an effective learning algorithm. One well-established approach, known as mean field theory, represents the stochastic distribution using a factorized approximation. However, the corresponding learning algorithm often fails to find a good solution. We conjecture that this is due to the implicit uni-modality of the mean field approximation which is therefore unable to capture multi-modality in the true distribution. In this paper we use variational methods to approximate the stochastic distribution using multi-modal mixtures of factorized distributions. We present results for both inference and learning to demonstrate the effectiveness of this approach.
Variational Relevance Vector Machines
Jan 16, 2013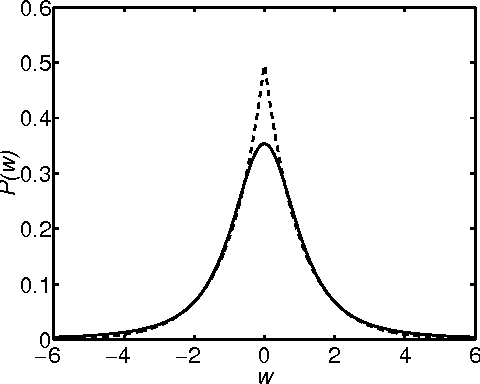

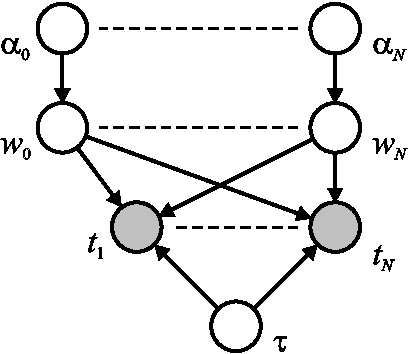
Abstract:The Support Vector Machine (SVM) of Vapnik (1998) has become widely established as one of the leading approaches to pattern recognition and machine learning. It expresses predictions in terms of a linear combination of kernel functions centred on a subset of the training data, known as support vectors. Despite its widespread success, the SVM suffers from some important limitations, one of the most significant being that it makes point predictions rather than generating predictive distributions. Recently Tipping (1999) has formulated the Relevance Vector Machine (RVM), a probabilistic model whose functional form is equivalent to the SVM. It achieves comparable recognition accuracy to the SVM, yet provides a full predictive distribution, and also requires substantially fewer kernel functions. The original treatment of the RVM relied on the use of type II maximum likelihood (the `evidence framework') to provide point estimates of the hyperparameters which govern model sparsity. In this paper we show how the RVM can be formulated and solved within a completely Bayesian paradigm through the use of variational inference, thereby giving a posterior distribution over both parameters and hyperparameters. We demonstrate the practicality and performance of the variational RVM using both synthetic and real world examples.
Bayesian Hierarchical Mixtures of Experts
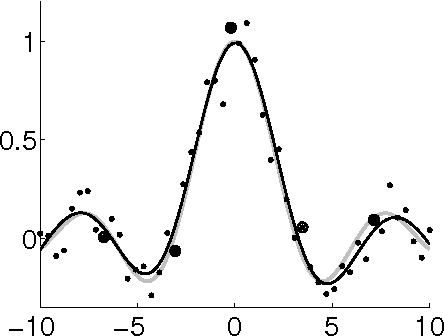
Oct 19, 2012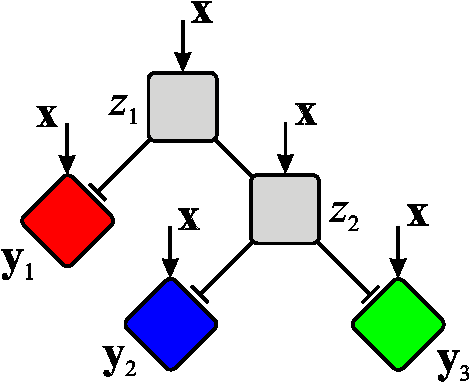
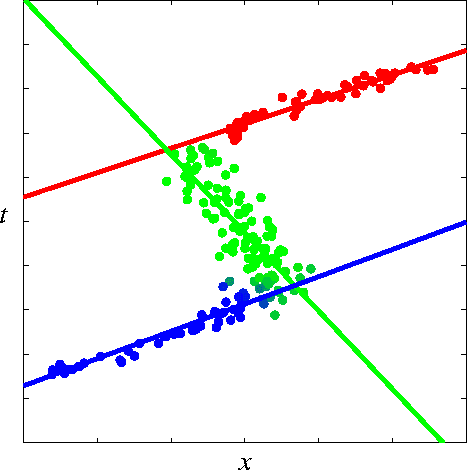
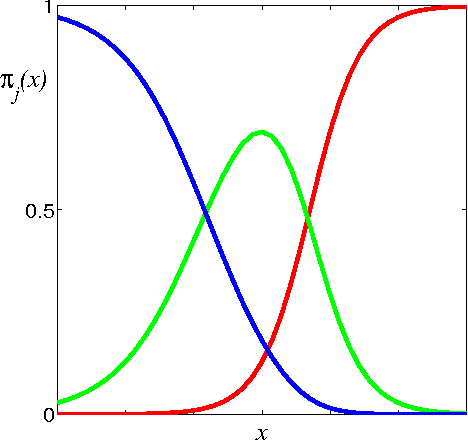
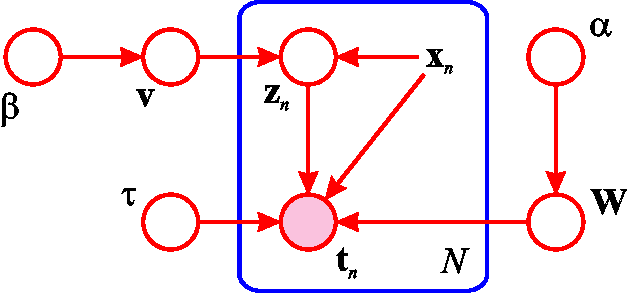
Abstract:The Hierarchical Mixture of Experts (HME) is a well-known tree-based model for regression and classification, based on soft probabilistic splits. In its original formulation it was trained by maximum likelihood, and is therefore prone to over-fitting. Furthermore the maximum likelihood framework offers no natural metric for optimizing the complexity and structure of the tree. Previous attempts to provide a Bayesian treatment of the HME model have relied either on ad-hoc local Gaussian approximations or have dealt with related models representing the joint distribution of both input and output variables. In this paper we describe a fully Bayesian treatment of the HME model based on variational inference. By combining local and global variational methods we obtain a rigourous lower bound on the marginal probability of the data under the model. This bound is optimized during the training phase, and its resulting value can be used for model order selection. We present results using this approach for a data set describing robot arm kinematics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge