Athanor: Local Search over Abstract Constraint Specifications

Local search is a common method for solving combinatorial optimisation problems. We focus on general-purpose local search solvers that accept as input a constraint model - a declarative description of a problem consisting of a set of decision variables under a set of constraints. Existing approaches typically take as input models written in solver-independent constraint modelling languages like MiniZinc. The Athanor solver we describe herein differs in that it begins from a specification of a problem in the abstract constraint specification language Essence, which allows problems to be described without commitment to low-level modelling decisions through its support for a rich set of abstract types. The advantage of proceeding from Essence is that the structure apparent in a concise, abstract specification of a problem can be exploited to generate high quality neighbourhoods automatically, avoiding the difficult task of identifying that structure in an equivalent constraint model. Based on the twin benefits of neighbourhoods derived from high level types and the scalability derived by searching directly over those types, our empirical results demonstrate strong performance in practice relative to existing solution methods.

Automatic Tabulation in Constraint Models

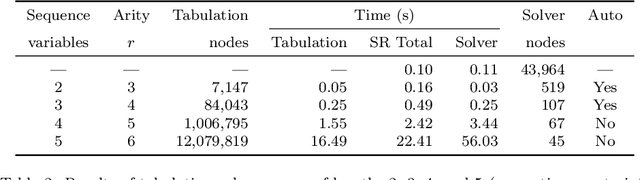
The performance of a constraint model can often be improved by converting a subproblem into a single table constraint. In this paper we study heuristics for identifying promising candidate subproblems, where converting the candidate into a table constraint is likely to improve solver performance. We propose a small set of heuristics to identify common cases, such as expressions that will propagate weakly. The process of discovering promising subproblems and tabulating them is entirely automated in the constraint modelling tool Savile Row. Caches are implemented to avoid tabulating equivalent subproblems many times. We give a simple algorithm to generate table constraints directly from a constraint expression in \savilerow. We demonstrate good performance on the benchmark problems used in earlier work on tabulation, and also for several new problem classes. In some cases, the entirely automated process leads to orders of magnitude improvements in solver performance.

Towards Reformulating Essence Specifications for Robustness

The Essence language allows a user to specify a constraint problem at a level of abstraction above that at which constraint modelling decisions are made. Essence specifications are refined into constraint models using the Conjure automated modelling tool, which employs a suite of refinement rules. However, Essence is a rich language in which there are many equivalent ways to specify a given problem. A user may therefore omit the use of domain attributes or abstract types, resulting in fewer refinement rules being applicable and therefore a reduced set of output models from which to select. This paper addresses the problem of recovering this information automatically to increase the robustness of the quality of the output constraint models in the face of variation in the input Essence specification. We present reformulation rules that can change the type of a decision variable or add attributes that shrink its domain. We demonstrate the efficacy of this approach in terms of the quantity and quality of models Conjure can produce from the transformed specification compared with the original.

Using Small MUSes to Explain How to Solve Pen and Paper Puzzles

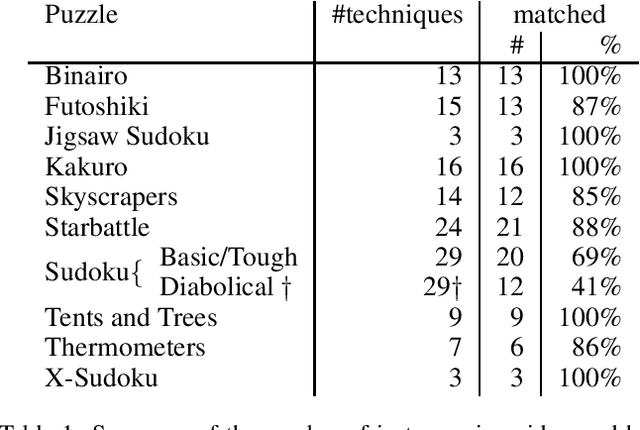
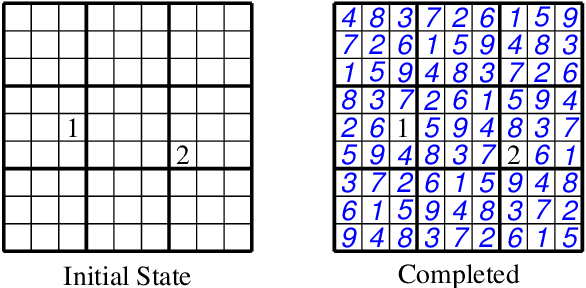
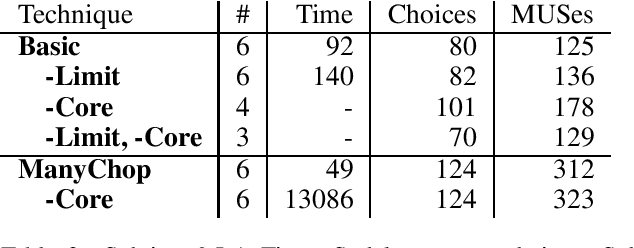
Pen and paper puzzles like Sudoku, Futoshiki and Skyscrapers are hugely popular. Solving such puzzles can be a trivial task for modern AI systems. However, most AI systems solve problems using a form of backtracking, while people try to avoid backtracking as much as possible. This means that existing AI systems do not output explanations about their reasoning that are meaningful to people. We present Demystify, a tool which allows puzzles to be expressed in a high-level constraint programming language and uses MUSes to allow us to produce descriptions of steps in the puzzle solving. We give several improvements to the existing techniques for solving puzzles with MUSes, which allow us to solve a range of significantly more complex puzzles and give higher quality explanations. We demonstrate the effectiveness and generality of Demystify by comparing its results to documented strategies for solving a range of pen and paper puzzles by hand, showing that our technique can find many of the same explanations.

Short and Long Supports for Constraint Propagation

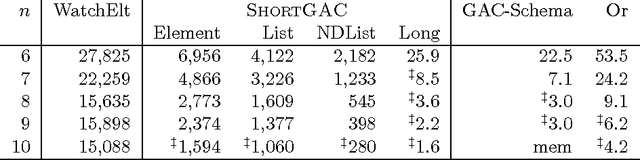
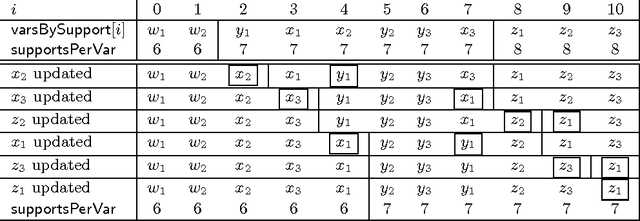
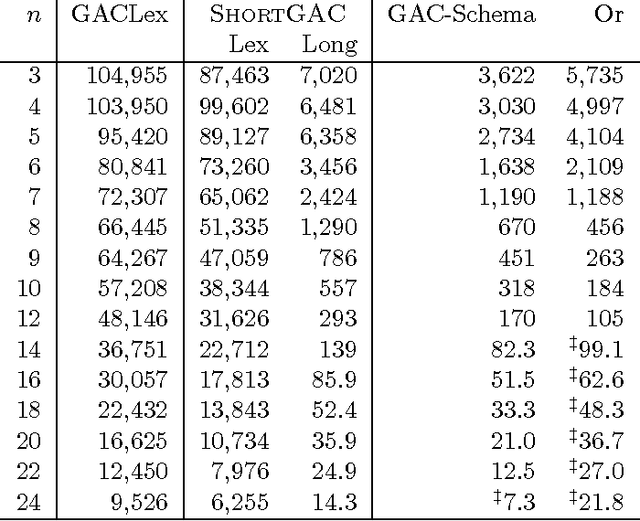
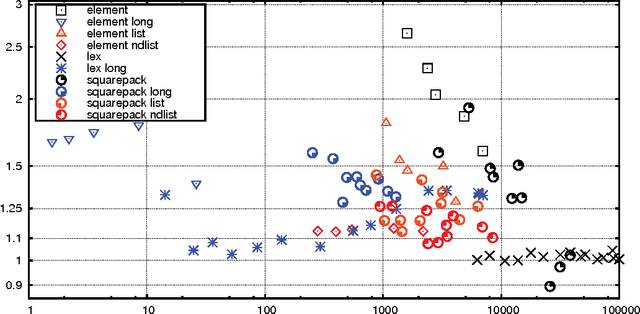
Special-purpose constraint propagation algorithms frequently make implicit use of short supports -- by examining a subset of the variables, they can infer support (a justification that a variable-value pair may still form part of an assignment that satisfies the constraint) for all other variables and values and save substantial work -- but short supports have not been studied in their own right. The two main contributions of this paper are the identification of short supports as important for constraint propagation, and the introduction of HaggisGAC, an efficient and effective general purpose propagation algorithm for exploiting short supports. Given the complexity of HaggisGAC, we present it as an optimised version of a simpler algorithm ShortGAC. Although experiments demonstrate the efficiency of ShortGAC compared with other general-purpose propagation algorithms where a compact set of short supports is available, we show theoretically and experimentally that HaggisGAC is even better. We also find that HaggisGAC performs better than GAC-Schema on full-length supports. We also introduce a variant algorithm HaggisGAC-Stable, which is adapted to avoid work on backtracking and in some cases can be faster and have significant reductions in memory use. All the proposed algorithms are excellent for propagating disjunctions of constraints. In all experiments with disjunctions we found our algorithms to be faster than Constructive Or and GAC-Schema by at least an order of magnitude, and up to three orders of magnitude.