Denoising Multi-Similarity Formulation: A Self-paced Curriculum-Driven Approach for Robust Metric Learning

Deep Metric Learning (DML) is a group of techniques that aim to measure the similarity between objects through the neural network. Although the number of DML methods has rapidly increased in recent years, most previous studies cannot effectively handle noisy data, which commonly exists in practical applications and often leads to serious performance deterioration. To overcome this limitation, in this paper, we build a connection between noisy samples and hard samples in the framework of self-paced learning, and propose a \underline{B}alanced \underline{S}elf-\underline{P}aced \underline{M}etric \underline{L}earning (BSPML) algorithm with a denoising multi-similarity formulation, where noisy samples are treated as extremely hard samples and adaptively excluded from the model training by sample weighting. Especially, due to the pairwise relationship and a new balance regularization term, the sub-problem \emph{w.r.t.} sample weights is a nonconvex quadratic function. To efficiently solve this nonconvex quadratic problem, we propose a doubly stochastic projection coordinate gradient algorithm. Importantly, we theoretically prove the convergence not only for the doubly stochastic projection coordinate gradient algorithm, but also for our BSPML algorithm. Experimental results on several standard data sets demonstrate that our BSPML algorithm has better generalization ability and robustness than the state-of-the-art robust DML approaches.

Balanced Self-Paced Learning for AUC Maximization

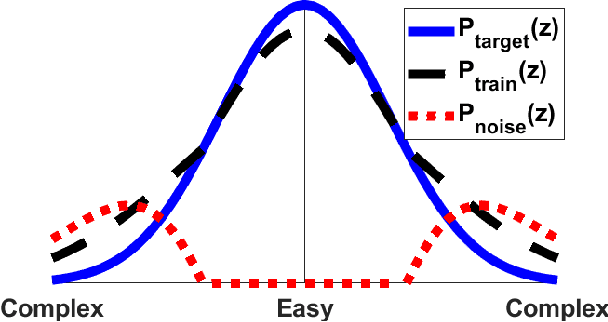
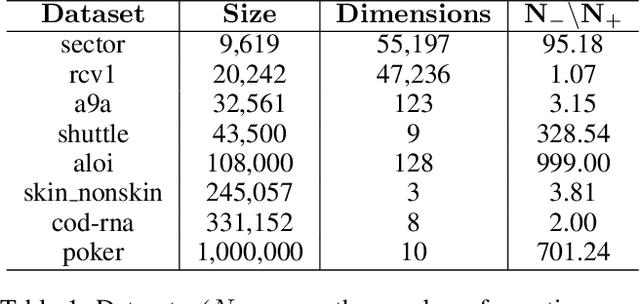
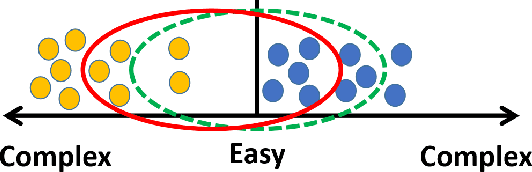
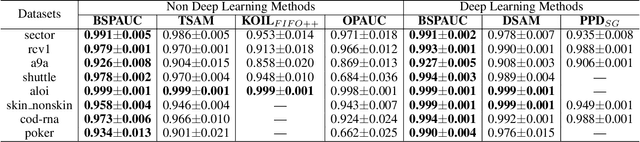
Learning to improve AUC performance is an important topic in machine learning. However, AUC maximization algorithms may decrease generalization performance due to the noisy data. Self-paced learning is an effective method for handling noisy data. However, existing self-paced learning methods are limited to pointwise learning, while AUC maximization is a pairwise learning problem. To solve this challenging problem, we innovatively propose a balanced self-paced AUC maximization algorithm (BSPAUC). Specifically, we first provide a statistical objective for self-paced AUC. Based on this, we propose our self-paced AUC maximization formulation, where a novel balanced self-paced regularization term is embedded to ensure that the selected positive and negative samples have proper proportions. Specially, the sub-problem with respect to all weight variables may be non-convex in our formulation, while the one is normally convex in existing self-paced problems. To address this, we propose a doubly cyclic block coordinate descent method. More importantly, we prove that the sub-problem with respect to all weight variables converges to a stationary point on the basis of closed-form solutions, and our BSPAUC converges to a stationary point of our fixed optimization objective under a mild assumption. Considering both the deep learning and kernel-based implementations, experimental results on several large-scale datasets demonstrate that our BSPAUC has a better generalization performance than existing state-of-the-art AUC maximization methods.