Neural Experts: Mixture of Experts for Implicit Neural Representations

Implicit neural representations (INRs) have proven effective in various tasks including image, shape, audio, and video reconstruction. These INRs typically learn the implicit field from sampled input points. This is often done using a single network for the entire domain, imposing many global constraints on a single function. In this paper, we propose a mixture of experts (MoE) implicit neural representation approach that enables learning local piece-wise continuous functions that simultaneously learns to subdivide the domain and fit locally. We show that incorporating a mixture of experts architecture into existing INR formulations provides a boost in speed, accuracy, and memory requirements. Additionally, we introduce novel conditioning and pretraining methods for the gating network that improves convergence to the desired solution. We evaluate the effectiveness of our approach on multiple reconstruction tasks, including surface reconstruction, image reconstruction, and audio signal reconstruction and show improved performance compared to non-MoE methods.

Exploiting Problem Structure in Deep Declarative Networks: Two Case Studies

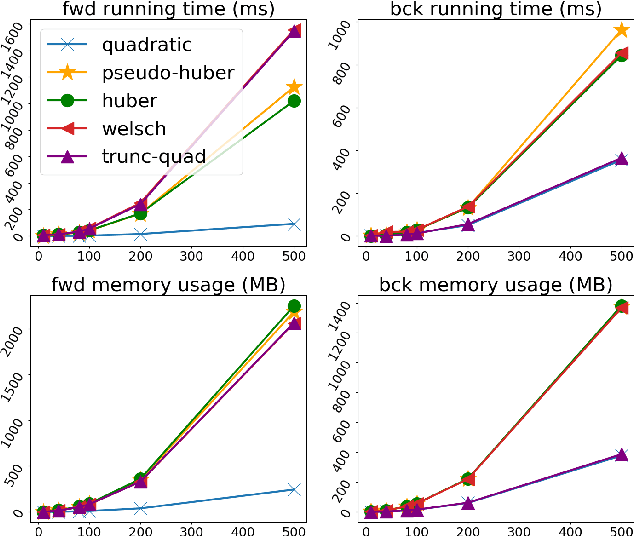
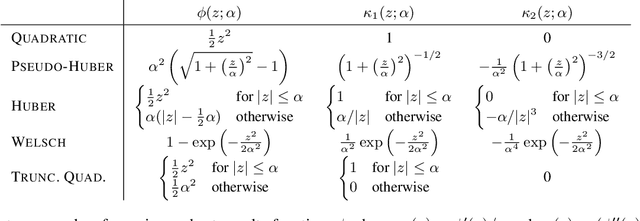
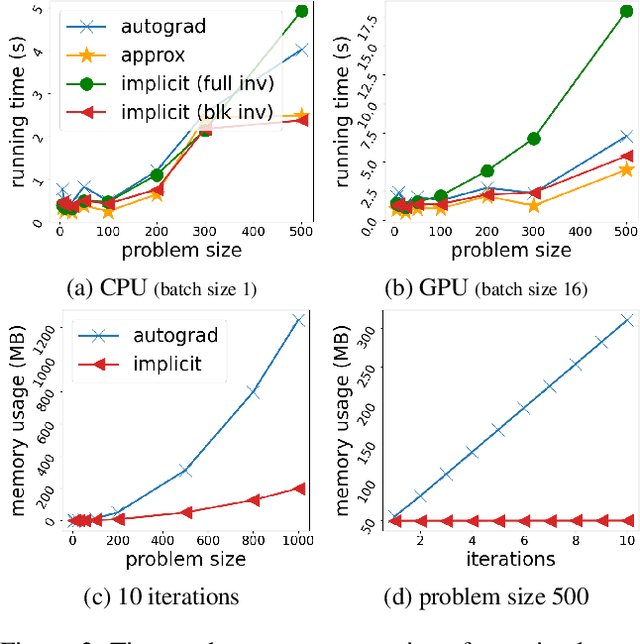
Deep declarative networks and other recent related works have shown how to differentiate the solution map of a (continuous) parametrized optimization problem, opening up the possibility of embedding mathematical optimization problems into end-to-end learnable models. These differentiability results can lead to significant memory savings by providing an expression for computing the derivative without needing to unroll the steps of the forward-pass optimization procedure during the backward pass. However, the results typically require inverting a large Hessian matrix, which is computationally expensive when implemented naively. In this work we study two applications of deep declarative networks -- robust vector pooling and optimal transport -- and show how problem structure can be exploited to obtain very efficient backward pass computations in terms of both time and memory. Our ideas can be used as a guide for improving the computational performance of other novel deep declarative nodes.

DiGS : Divergence guided shape implicit neural representation for unoriented point clouds

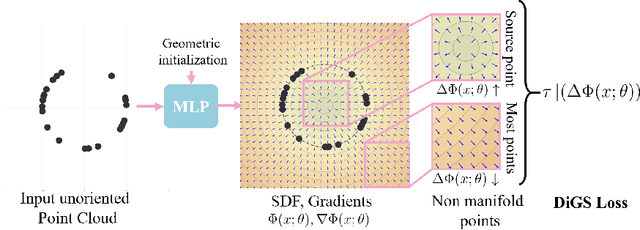
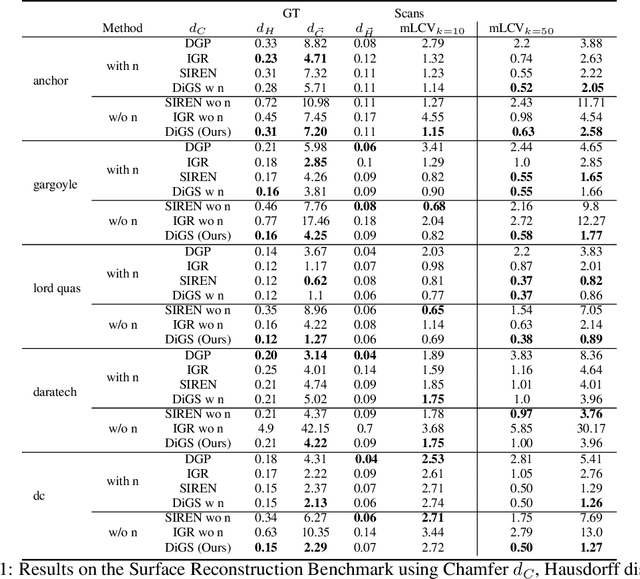
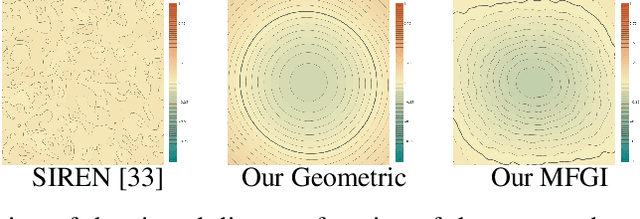
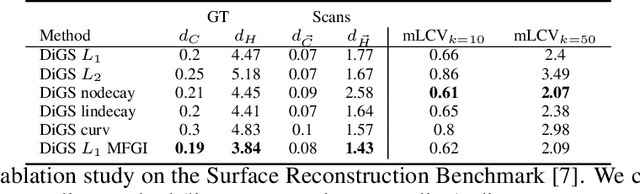
Neural shape representations have recently shown to be effective in shape analysis and reconstruction tasks. Existing neural network methods require point coordinates and corresponding normal vectors to learn the implicit level sets of the shape. Normal vectors are often not provided as raw data, therefore, approximation and reorientation are required as pre-processing stages, both of which can introduce noise. In this paper, we propose a divergence guided shape representation learning approach that does not require normal vectors as input. We show that incorporating a soft constraint on the divergence of the distance function favours smooth solutions that reliably orients gradients to match the unknown normal at each point, in some cases even better than approaches that use ground truth normal vectors directly. Additionally, we introduce a novel geometric initialization method for sinusoidal shape representation networks that further improves convergence to the desired solution. We evaluate the effectiveness of our approach on the task of surface reconstruction and show state-of-the-art performance compared to other unoriented methods and on-par performance compared to oriented methods.

Computer Assisted Composition in Continuous Time

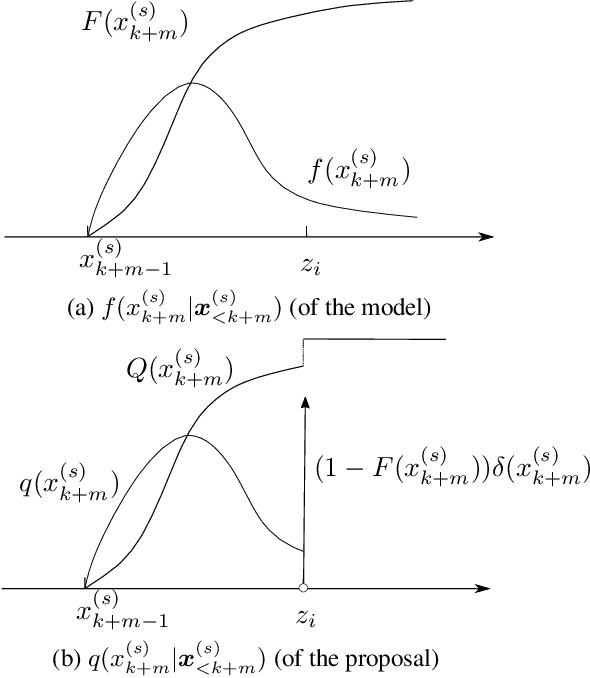
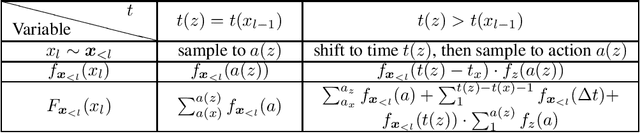
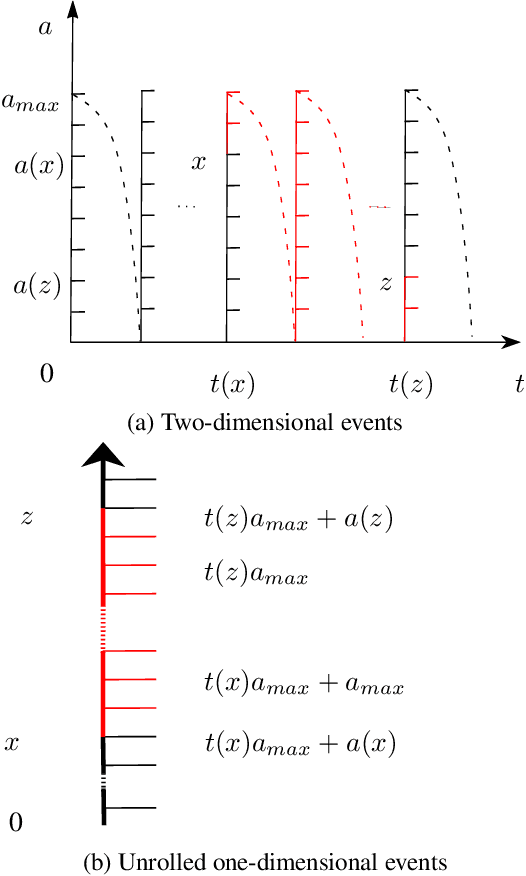
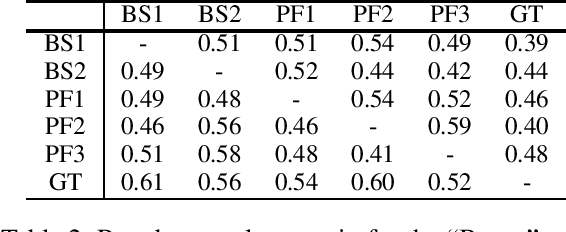
We address the problem of combining sequence models of symbolic music with user defined constraints. For typical models this is non-trivial as only the conditional distribution of each symbol given the earlier symbols is available, while the constraints correspond to arbitrary times. Previously this has been addressed by assuming a discrete time model of fixed rhythm. We generalise to continuous time and arbitrary rhythm by introducing a simple, novel, and efficient particle filter scheme, applicable to general continuous time point processes. Extensive experimental evaluations demonstrate that in comparison with a more traditional beam search baseline, the particle filter exhibits superior statistical properties and yields more agreeable results in an extensive human listening test experiment.