Deep Involutive Generative Models for Neural MCMC
Paper and Code
Jul 02, 2020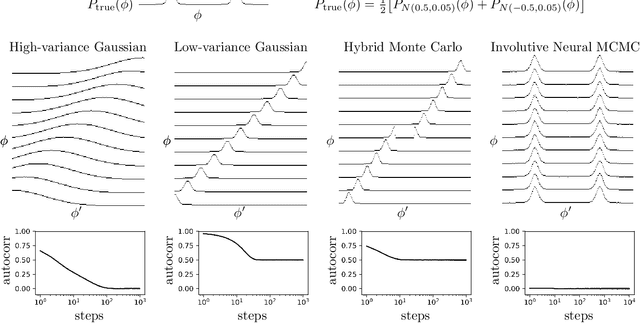
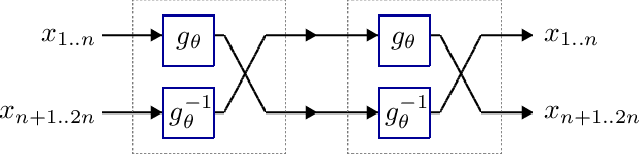
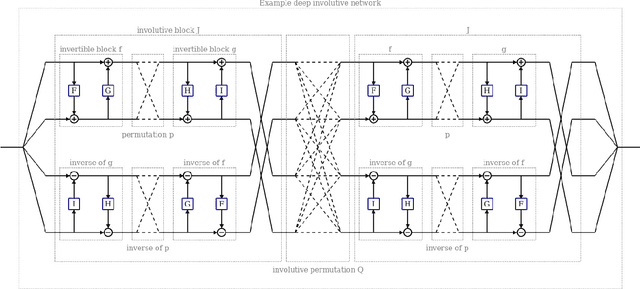

We introduce deep involutive generative models, a new architecture for deep generative modeling, and use them to define Involutive Neural MCMC, a new approach to fast neural MCMC. An involutive generative model represents a probability kernel $G(\phi \mapsto \phi')$ as an involutive (i.e., self-inverting) deterministic function $f(\phi, \pi)$ on an enlarged state space containing auxiliary variables $\pi$. We show how to make these models volume preserving, and how to use deep volume-preserving involutive generative models to make valid Metropolis-Hastings updates based on an auxiliary variable scheme with an easy-to-calculate acceptance ratio. We prove that deep involutive generative models and their volume-preserving special case are universal approximators for probability kernels. This result implies that with enough network capacity and training time, they can be used to learn arbitrarily complex MCMC updates. We define a loss function and optimization algorithm for training parameters given simulated data. We also provide initial experiments showing that Involutive Neural MCMC can efficiently explore multi-modal distributions that are intractable for Hybrid Monte Carlo, and can converge faster than A-NICE-MC, a recently introduced neural MCMC technique.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge