High dimensional stochastic linear contextual bandit with missing covariates

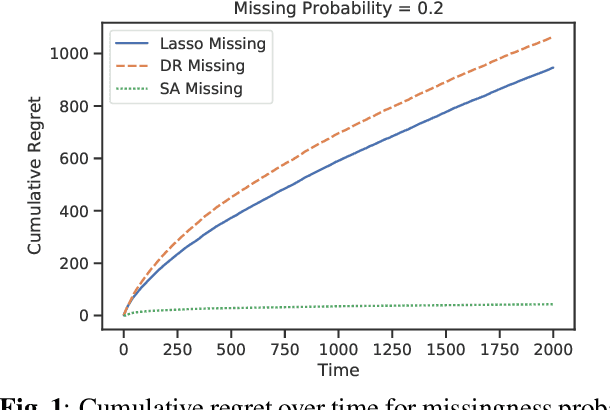
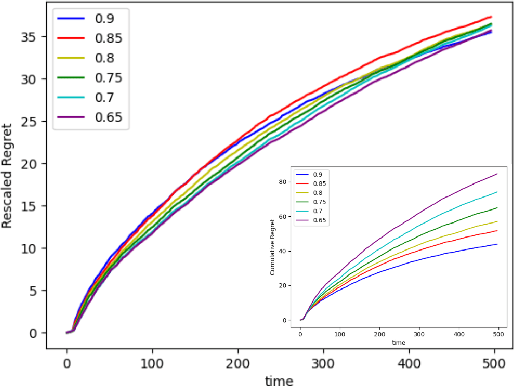
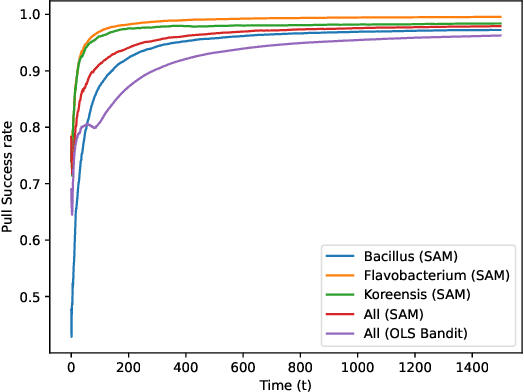
Recent works in bandit problems adopted lasso convergence theory in the sequential decision-making setting. Even with fully observed contexts, there are technical challenges that hinder the application of existing lasso convergence theory: 1) proving the restricted eigenvalue condition under conditionally sub-Gaussian noise and 2) accounting for the dependence between the context variables and the chosen actions. This paper studies the effect of missing covariates on regret for stochastic linear bandit algorithms. Our work provides a high-probability upper bound on the regret incurred by the proposed algorithm in terms of covariate sampling probabilities, showing that the regret degrades due to missingness by at most $\zeta_{min}^2$, where $\zeta_{min}$ is the minimum probability of observing covariates in the context vector. We illustrate our algorithm for the practical application of experimental design for collecting gene expression data by a sequential selection of class discriminating DNA probes.

The Sylvester Graphical Lasso (SyGlasso)

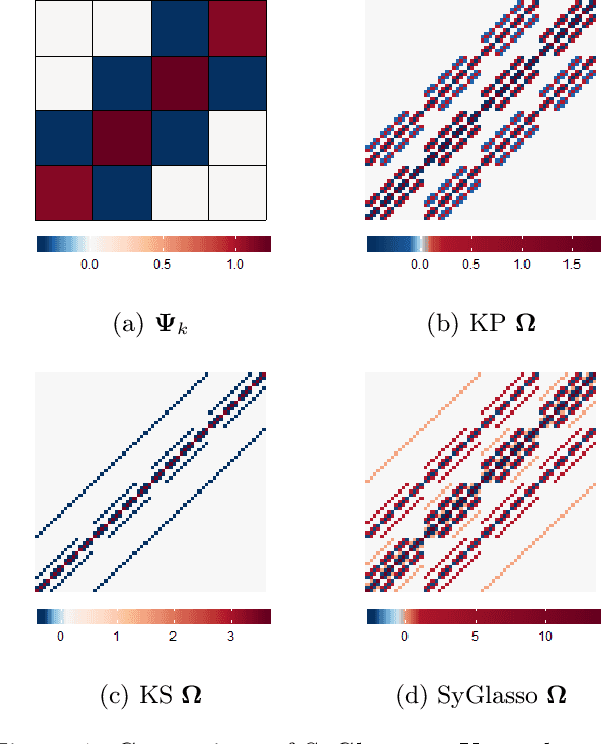
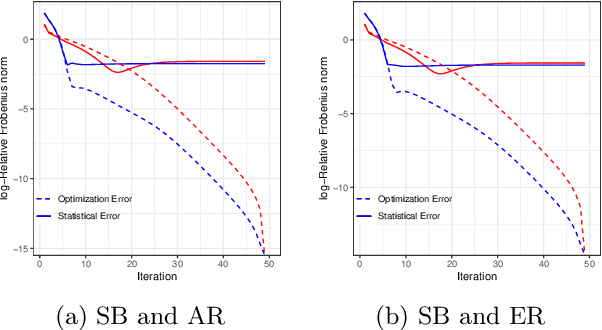
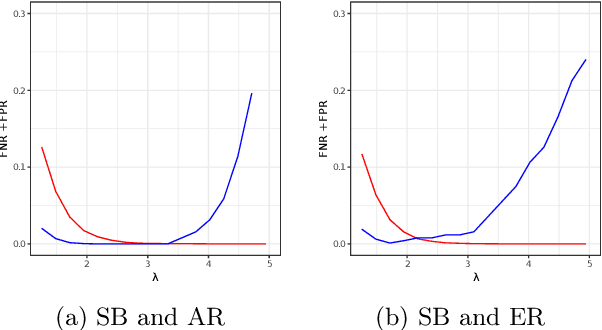
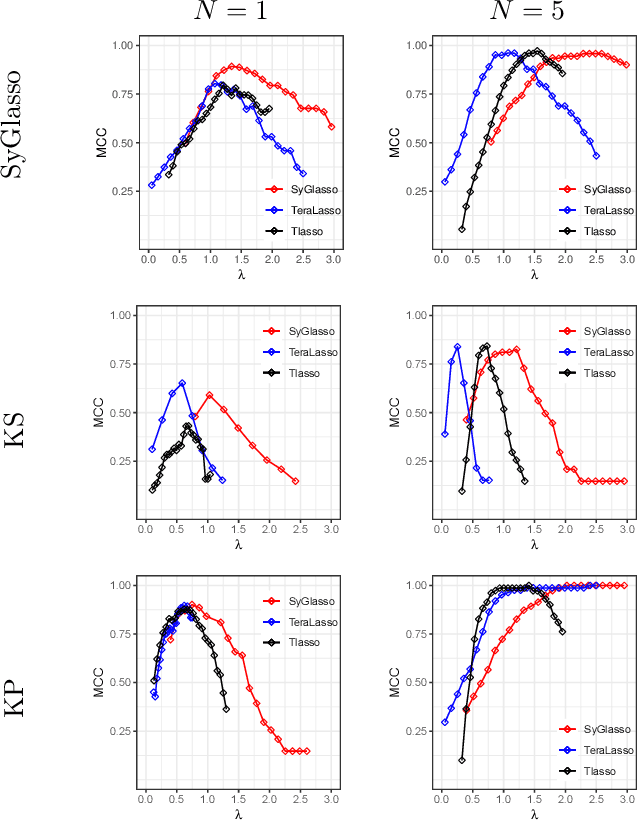
This paper introduces the Sylvester graphical lasso (SyGlasso) that captures multiway dependencies present in tensor-valued data. The model is based on the Sylvester equation that defines a generative model. The proposed model complements the tensor graphical lasso (Greenewald et al., 2019) that imposes a Kronecker sum model for the inverse covariance matrix by providing an alternative Kronecker sum model that is generative and interpretable. A nodewise regression approach is adopted for estimating the conditional independence relationships among variables. The statistical convergence of the method is established, and empirical studies are provided to demonstrate the recovery of meaningful conditional dependency graphs. We apply the SyGlasso to an electroencephalography (EEG) study to compare the brain connectivity of alcoholic and nonalcoholic subjects. We demonstrate that our model can simultaneously estimate both the brain connectivity and its temporal dependencies.

Precision Matrix Estimation with Noisy and Missing Data

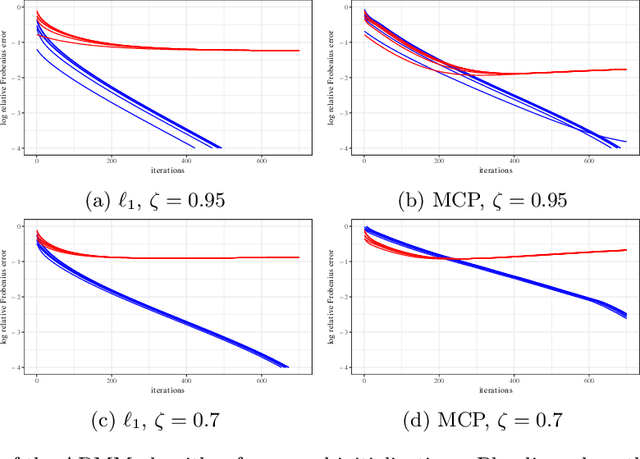
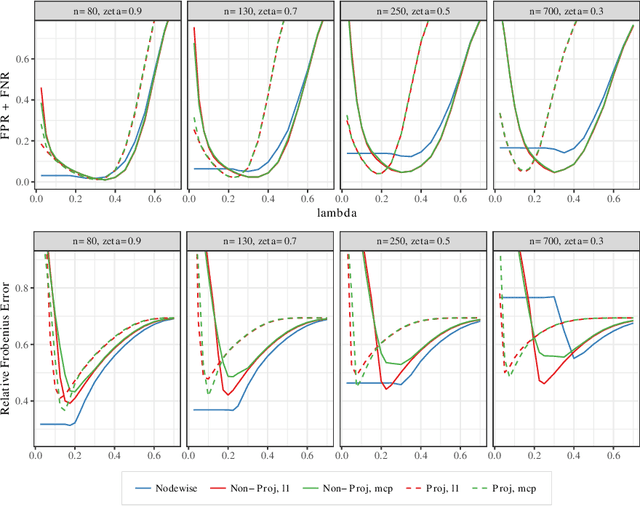
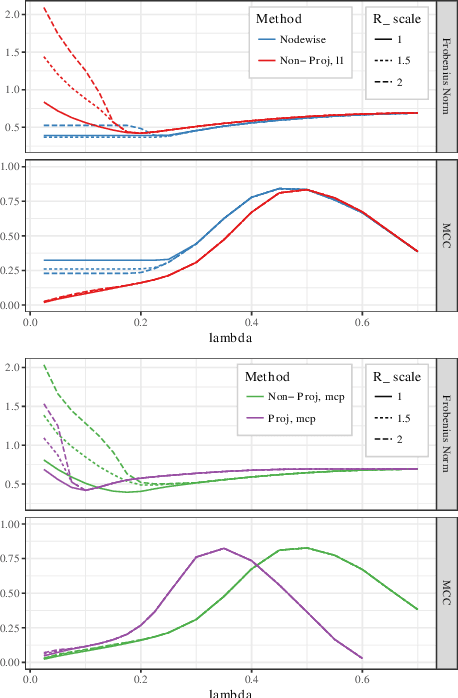
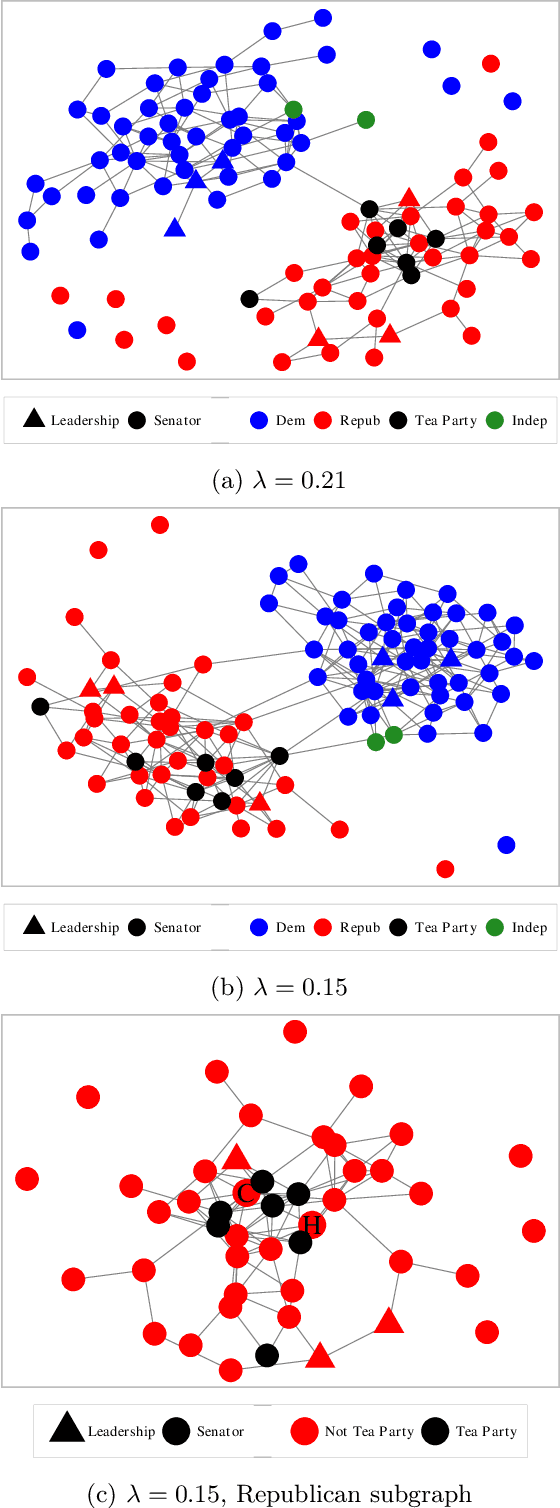
Estimating conditional dependence graphs and precision matrices are some of the most common problems in modern statistics and machine learning. When data are fully observed, penalized maximum likelihood-type estimators have become standard tools for estimating graphical models under sparsity conditions. Extensions of these methods to more complex settings where data are contaminated with additive or multiplicative noise have been developed in recent years. In these settings, however, the relative performance of different methods is not well understood and algorithmic gaps still exist. In particular, in high-dimensional settings these methods require using non-positive semidefinite matrices as inputs, presenting novel optimization challenges. We develop an alternating direction method of multipliers (ADMM) algorithm for these problems, providing a feasible algorithm to estimate precision matrices with indefinite input and potentially nonconvex penalties. We compare this method with existing alternative solutions and empirically characterize the tradeoffs between them. Finally, we use this method to explore the networks among US senators estimated from voting records data.

Minimum Volume Topic Modeling

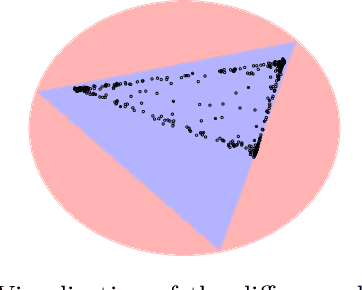
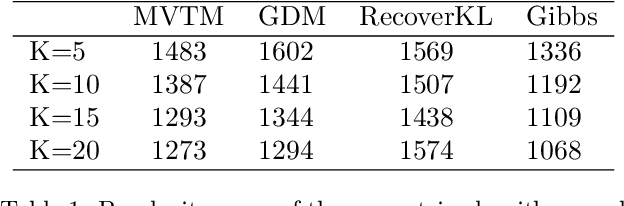
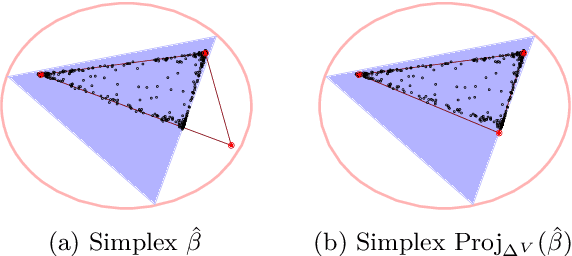
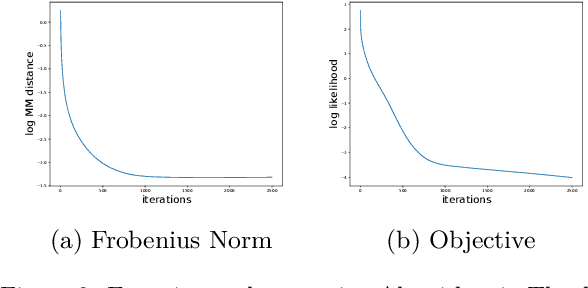
We propose a new topic modeling procedure that takes advantage of the fact that the Latent Dirichlet Allocation (LDA) log likelihood function is asymptotically equivalent to the logarithm of the volume of the topic simplex. This allows topic modeling to be reformulated as finding the probability simplex that minimizes its volume and encloses the documents that are represented as distributions over words. A convex relaxation of the minimum volume topic model optimization is proposed, and it is shown that the relaxed problem has the same global minimum as the original problem under the separability assumption and the sufficiently scattered assumption introduced by Arora et al. (2013) and Huang et al. (2016). A locally convergent alternating direction method of multipliers (ADMM) approach is introduced for solving the relaxed minimum volume problem. Numerical experiments illustrate the benefits of our approach in terms of computation time and topic recovery performance.