Contextures: Representations from Contexts

Despite the empirical success of foundation models, we do not have a systematic characterization of the representations that these models learn. In this paper, we establish the contexture theory. It shows that a large class of representation learning methods can be characterized as learning from the association between the input and a context variable. Specifically, we show that many popular methods aim to approximate the top-d singular functions of the expectation operator induced by the context, in which case we say that the representation learns the contexture. We demonstrate the generality of the contexture theory by proving that representation learning within various learning paradigms -- supervised, self-supervised, and manifold learning -- can all be studied from such a perspective. We also prove that the representations that learn the contexture are optimal on those tasks that are compatible with the context. One important implication of the contexture theory is that once the model is large enough to approximate the top singular functions, further scaling up the model size yields diminishing returns. Therefore, scaling is not all we need, and further improvement requires better contexts. To this end, we study how to evaluate the usefulness of a context without knowing the downstream tasks. We propose a metric and show by experiments that it correlates well with the actual performance of the encoder on many real datasets.

Score-based Causal Representation Learning with Interventions

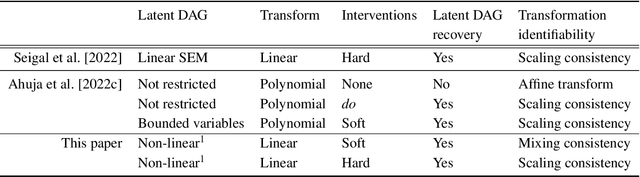
This paper studies causal representation learning problem when the latent causal variables are observed indirectly through an unknown linear transformation. The objectives are: (i) recovering the unknown linear transformation (up to scaling and ordering), and (ii) determining the directed acyclic graph (DAG) underlying the latent variables. Since identifiable representation learning is impossible based on only observational data, this paper uses both observational and interventional data. The interventional data is generated under distinct single-node randomized hard and soft interventions. These interventions are assumed to cover all nodes in the latent space. It is established that the latent DAG structure can be recovered under soft randomized interventions via the following two steps. First, a set of transformation candidates is formed by including all inverting transformations corresponding to which the \emph{score} function of the transformed variables has the minimal number of coordinates that change between an interventional and the observational environment summed over all pairs. Subsequently, this set is distilled using a simple constraint to recover the latent DAG structure. For the special case of hard randomized interventions, with an additional hypothesis testing step, one can also uniquely recover the linear transformation, up to scaling and a valid causal ordering. These results generalize the recent results that either assume deterministic hard interventions or linear causal relationships in the latent space.

Causal Bandits for Linear Structural Equation Models

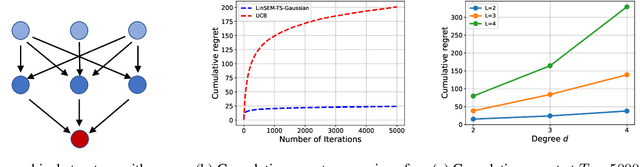
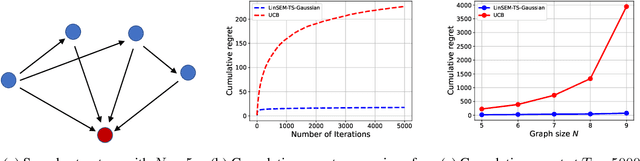
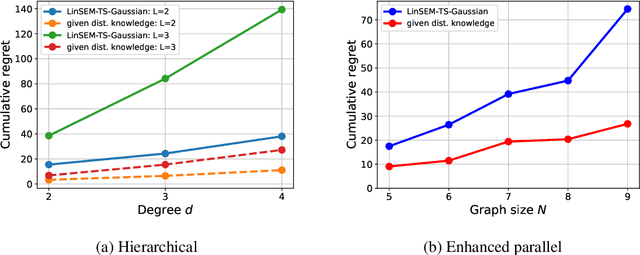
This paper studies the problem of designing an optimal sequence of interventions in a causal graphical model to minimize the cumulative regret with respect to the best intervention in hindsight. This is, naturally, posed as a causal bandit problem. The focus is on causal bandits for linear structural equation models (SEMs) and soft interventions. It is assumed that the graph's structure is known, and it has $N$ nodes. Two linear mechanisms, one soft intervention and one observational, are assumed for each node, giving rise to $2^N$ possible interventions. The existing causal bandit algorithms assume that at least the interventional distributions of the reward node's parents are fully specified. However, there are $2^N$ such distributions (one corresponding to each intervention), acquiring which becomes prohibitive even in moderate-sized graphs. This paper dispenses with the assumption of knowing these distributions. Two algorithms are proposed for the frequentist (UCB-based) and Bayesian (Thompson Sampling-based) settings. The key idea of these algorithms is to avoid directly estimating the $2^N$ reward distributions and instead estimate the parameters that fully specify the SEMs (linear in $N$) and use them to compute the rewards. In both algorithms, under boundedness assumptions on noise and the parameter space, the cumulative regrets scale as $\tilde{\cal O} ((2d)^L L \sqrt{T})$, where $d$ is the graph's maximum degree, and $L$ is the length of its longest causal path.

Scalable Intervention Target Estimation in Linear Models

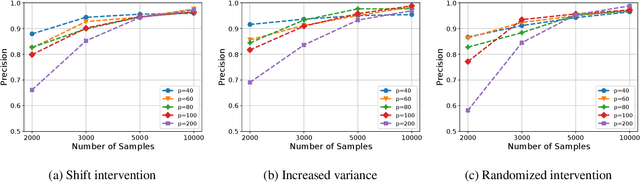
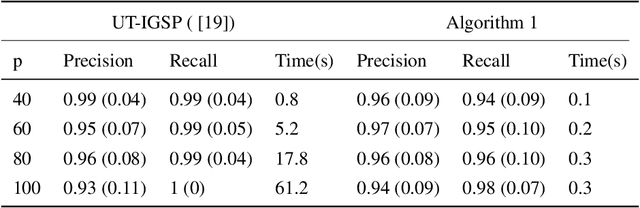
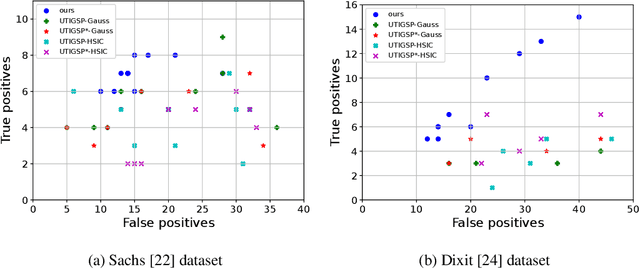
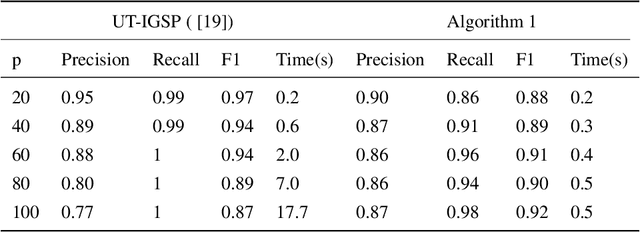
This paper considers the problem of estimating the unknown intervention targets in a causal directed acyclic graph from observational and interventional data. The focus is on soft interventions in linear structural equation models (SEMs). Current approaches to causal structure learning either work with known intervention targets or use hypothesis testing to discover the unknown intervention targets even for linear SEMs. This severely limits their scalability and sample complexity. This paper proposes a scalable and efficient algorithm that consistently identifies all intervention targets. The pivotal idea is to estimate the intervention sites from the difference between the precision matrices associated with the observational and interventional datasets. It involves repeatedly estimating such sites in different subsets of variables. The proposed algorithm can be used to also update a given observational Markov equivalence class into the interventional Markov equivalence class. Consistency, Markov equivalency, and sample complexity are established analytically. Finally, simulation results on both real and synthetic data demonstrate the gains of the proposed approach for scalable causal structure recovery. Implementation of the algorithm and the code to reproduce the simulation results are available at \url{https://github.com/bvarici/intervention-estimation}.