A Control Theory inspired Exploration Method for a Linear Bandit driven by a Linear Gaussian Dynamical System

The paper introduces a linear bandit environment where the reward is the output of a known Linear Gaussian Dynamical System (LGDS). In this environment, we address the fundamental challenge of balancing exploration -- gathering information about the environment -- and exploitation -- selecting to the action with the highest predicted reward. We propose two algorithms, Kalman filter Upper Confidence Bound (Kalman-UCB) and Information filter Directed Exploration Action-selection (IDEA). Kalman-UCB uses the principle of optimism in the face of uncertainty. IDEA selects actions that maximize the combination of the predicted reward and a term that quantifies how much an action minimizes the error of the Kalman filter state prediction, which depends on the LGDS property called observability. IDEA is motivated by applications such as hyperparameter optimization in machine learning. A major problem encountered in hyperparameter optimization is the large action spaces, which hinder the performance of methods inspired by principle of optimism in the face of uncertainty as they need to explore each action to lower reward prediction uncertainty. To predict if either Kalman-UCB or IDEA will perform better, a metric based on the LGDS properties is provided. This metric is validated with numerical results across a variety of randomly generated environments.

A Data-Integrated Framework for Learning Fractional-Order Nonlinear Dynamical Systems

This paper presents a data-integrated framework for learning the dynamics of fractional-order nonlinear systems in both discrete-time and continuous-time settings. The proposed framework consists of two main steps. In the first step, input-output experiments are designed to generate the necessary datasets for learning the system dynamics, including the fractional order, the drift vector field, and the control vector field. In the second step, these datasets, along with the memory-dependent property of fractional-order systems, are used to estimate the system's fractional order. The drift and control vector fields are then reconstructed using orthonormal basis functions. To validate the proposed approach, the algorithm is applied to four benchmark fractional-order systems. The results confirm the effectiveness of the proposed framework in learning the system dynamics accurately. Finally, the same datasets are used to learn equivalent integer-order models. The numerical comparisons demonstrate that fractional-order models better capture long-range dependencies, highlighting the limitations of integer-order representations.

HyperController: A Hyperparameter Controller for Fast and Stable Training of Reinforcement Learning Neural Networks

We introduce Hyperparameter Controller (HyperController), a computationally efficient algorithm for hyperparameter optimization during training of reinforcement learning neural networks. HyperController optimizes hyperparameters quickly while also maintaining improvement of the reinforcement learning neural network, resulting in faster training and deployment. It achieves this by modeling the hyperparameter optimization problem as an unknown Linear Gaussian Dynamical System, which is a system with a state that linearly changes. It then learns an efficient representation of the hyperparameter objective function using the Kalman filter, which is the optimal one-step predictor for a Linear Gaussian Dynamical System. To demonstrate the performance of HyperController, it is applied as a hyperparameter optimizer during training of reinforcement learning neural networks on a variety of OpenAI Gymnasium environments. In four out of the five Gymnasium environments, HyperController achieves highest median reward during evaluation compared to other algorithms. The results exhibit the potential of HyperController for efficient and stable training of reinforcement learning neural networks.

An Exploration-free Method for a Linear Stochastic Bandit Driven by a Linear Gaussian Dynamical System

In stochastic multi-armed bandits, a major problem the learner faces is the trade-off between exploration and exploitation. Recently, exploration-free methods -- methods that commit to the action predicted to return the highest reward -- have been studied from the perspective of linear bandits. In this paper, we introduce a linear bandit setting where the reward is the output of a linear Gaussian dynamical system. Motivated by a problem encountered in hyperparameter optimization for reinforcement learning, where the number of actions is much higher than the number of training iterations, we propose Kalman filter Observability Dependent Exploration (KODE), an exploration-free method that utilizes the Kalman filter predictions to select actions. Our major contribution of this work is our analysis of the performance of the proposed method, which is dependent on the observability properties of the underlying linear Gaussian dynamical system. We evaluate KODE via two different metrics: regret, which is the cumulative expected difference between the highest possible reward and the reward sampled by KODE, and action alignment, which measures how closely KODE's chosen action aligns with the linear Gaussian dynamical system's state variable. To provide intuition on the performance, we prove that KODE implicitly encourages the learner to explore actions depending on the observability of the linear Gaussian dynamical system. This method is compared to several well-known stochastic multi-armed bandit algorithms to validate our theoretical results.

Restless Bandit Problem with Rewards Generated by a Linear Gaussian Dynamical System

The stochastic multi-armed bandit problem studies decision-making under uncertainty. In the problem, the learner interacts with an environment by choosing an action at each round, where a round is an instance of an interaction. In response, the environment reveals a reward, which is sampled from a stochastic process, to the learner. The goal of the learner is to maximize cumulative reward. A specific variation of the stochastic multi-armed bandit problem is the restless bandit, where the reward for each action is sampled from a Markov chain. The restless bandit with a discrete state-space is a well-studied problem, but to the best of our knowledge, not many results exist for the continuous state-space version which has many applications such as hyperparameter optimization. In this work, we tackle the restless bandit with continuous state-space by assuming the rewards are the inner product of an action vector and a state vector generated by a linear Gaussian dynamical system. To predict the reward for each action, we propose a method that takes a linear combination of previously observed rewards for predicting each action's next reward. We show that, regardless of the sequence of previous actions chosen, the reward sampled for any previously chosen action can be used for predicting another action's future reward, i.e. the reward sampled for action 1 at round $t-1$ can be used for predicting the reward for action $2$ at round $t$. This is accomplished by designing a modified Kalman filter with a matrix representation that can be learned for reward prediction. Numerical evaluations are carried out on a set of linear Gaussian dynamical systems.

Beyond PCA: A Probabilistic Gram-Schmidt Approach to Feature Extraction

Linear feature extraction at the presence of nonlinear dependencies among the data is a fundamental challenge in unsupervised learning. We propose using a Probabilistic Gram-Schmidt (PGS) type orthogonalization process in order to detect and map out redundant dimensions. Specifically, by applying the PGS process over any family of functions which presumably captures the nonlinear dependencies in the data, we construct a series of covariance matrices that can either be used to remove those dependencies from the principal components, or to identify new large-variance directions. In the former case, we prove that under certain assumptions the resulting algorithms detect and remove nonlinear dependencies whenever those dependencies lie in the linear span of the chosen function family. In the latter, we provide information-theoretic guarantees in terms of entropy reduction. Both proposed methods extract linear features from the data while removing nonlinear redundancies. We provide simulation results on synthetic and real-world datasets which show improved performance over PCA and state-of-the-art linear feature extraction algorithms, both in terms of variance maximization of the extracted features, and in terms of improved performance of classification algorithms.

Towards Hyperparameter-Agnostic DNN Training via Dynamical System Insights

We present a stochastic first-order optimization method specialized for deep neural networks (DNNs), ECCO-DNN. This method models the optimization variable trajectory as a dynamical system and develops a discretization algorithm that adaptively selects step sizes based on the trajectory's shape. This provides two key insights: designing the dynamical system for fast continuous-time convergence and developing a time-stepping algorithm to adaptively select step sizes based on principles of numerical integration and neural network structure. The result is an optimizer with performance that is insensitive to hyperparameter variations and that achieves comparable performance to state-of-the-art optimizers including ADAM, SGD, RMSProp, and AdaGrad. We demonstrate this in training DNN models and datasets, including CIFAR-10 and CIFAR-100 using ECCO-DNN and find that ECCO-DNN's single hyperparameter can be changed by three orders of magnitude without affecting the trained models' accuracies. ECCO-DNN's insensitivity reduces the data and computation needed for hyperparameter tuning, making it advantageous for rapid prototyping and for applications with new datasets. To validate the efficacy of our proposed optimizer, we train an LSTM architecture on a household power consumption dataset with ECCO-DNN and achieve an optimal mean-square-error without tuning hyperparameters.

Model-Free Learning and Optimal Policy Design in Multi-Agent MDPs Under Probabilistic Agent Dropout

This work studies a multi-agent Markov decision process (MDP) that can undergo agent dropout and the computation of policies for the post-dropout system based on control and sampling of the pre-dropout system. The controller's objective is to find an optimal policy that maximizes the value of the expected system given a priori knowledge of the agents' dropout probabilities. Finding an optimal policy for any specific dropout realization is a special case of this problem. For MDPs with a certain transition independence and reward separability structure, we assume that removing agents from the system forms a new MDP comprised of the remaining agents with new state and action spaces, transition dynamics that marginalize the removed agents, and rewards that are independent of the removed agents. We first show that under these assumptions, the value of the expected post-dropout system can be represented by a single MDP; this "robust MDP" eliminates the need to evaluate all $2^N$ realizations of the system, where $N$ denotes the number of agents. More significantly, in a model-free context, it is shown that the robust MDP value can be estimated with samples generated by the pre-dropout system, meaning that robust policies can be found before dropout occurs. This fact is used to propose a policy importance sampling (IS) routine that performs policy evaluation for dropout scenarios while controlling the existing system with good pre-dropout policies. The policy IS routine produces value estimates for both the robust MDP and specific post-dropout system realizations and is justified with exponential confidence bounds. Finally, the utility of this approach is verified in simulation, showing how structural properties of agent dropout can help a controller find good post-dropout policies before dropout occurs.

Stochastic Multi-armed Bandits with Non-stationary Rewards Generated by a Linear Dynamical System

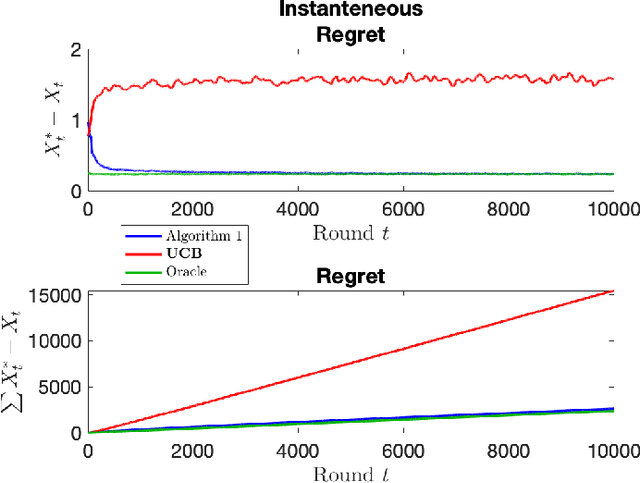
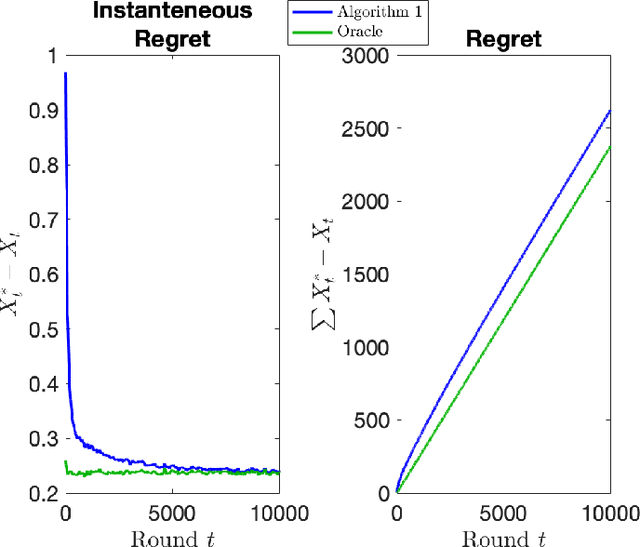
The stochastic multi-armed bandit has provided a framework for studying decision-making in unknown environments. We propose a variant of the stochastic multi-armed bandit where the rewards are sampled from a stochastic linear dynamical system. The proposed strategy for this stochastic multi-armed bandit variant is to learn a model of the dynamical system while choosing the optimal action based on the learned model. Motivated by mathematical finance areas such as Intertemporal Capital Asset Pricing Model proposed by Merton and Stochastic Portfolio Theory proposed by Fernholz that both model asset returns with stochastic differential equations, this strategy is applied to quantitative finance as a high-frequency trading strategy, where the goal is to maximize returns within a time period.

Toward Safe and Efficient Human-Robot Interaction via Behavior-Driven Danger Signaling

This paper introduces the notion of danger awareness in the context of Human-Robot Interaction (HRI), which decodes whether a human is aware of the existence of the robot, and illuminates whether the human is willing to engage in enforcing the safety. This paper also proposes a method to quantify this notion as a single binary variable, so-called danger awareness coefficient. By analyzing the effect of this coefficient on the human's actions, an online Bayesian learning method is proposed to update the belief about the value of the coefficient. It is shown that based upon the danger awareness coefficient and the proposed learning method, the robot can build a predictive human model to anticipate the human's future actions. In order to create a communication channel between the human and the robot, to enrich the observations and get informative data about the human, and to improve the efficiency of the robot, the robot is equipped with a danger signaling system. A predictive planning scheme, coupled with the predictive human model, is also proposed to provide an efficient and Probabilistically safe plan for the robot. The effectiveness of the proposed scheme is demonstrated through simulation studies on an interaction between a self-driving car and a pedestrian.