Learning Abduction under Partial Observability

Juba recently proposed a formulation of learning abductive reasoning from examples, in which both the relative plausibility of various explanations, as well as which explanations are valid, are learned directly from data. The main shortcoming of this formulation of the task is that it assumes access to full-information (i.e., fully specified) examples; relatedly, it offers no role for declarative background knowledge, as such knowledge is rendered redundant in the abduction task by complete information. In this work, we extend the formulation to utilize such partially specified examples, along with declarative background knowledge about the missing data. We show that it is possible to use implicitly learned rules together with the explicitly given declarative knowledge to support hypotheses in the course of abduction. We observe that when a small explanation exists, it is possible to obtain a much-improved guarantee in the challenging exception-tolerant setting. Such small, human-understandable explanations are of particular interest for potential applications of the task.

Efficient, Safe, and Probably Approximately Complete Learning of Action Models

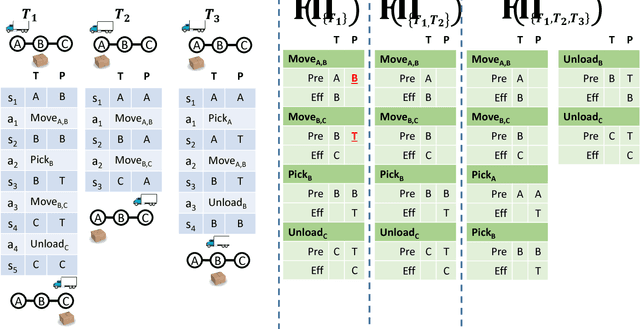
In this paper we explore the theoretical boundaries of planning in a setting where no model of the agent's actions is given. Instead of an action model, a set of successfully executed plans are given and the task is to generate a plan that is safe, i.e., guaranteed to achieve the goal without failing. To this end, we show how to learn a conservative model of the world in which actions are guaranteed to be applicable. This conservative model is then given to an off-the-shelf classical planner, resulting in a plan that is guaranteed to achieve the goal. However, this reduction from a model-free planning to a model-based planning is not complete: in some cases a plan will not be found even when such exists. We analyze the relation between the number of observed plans and the likelihood that our conservative approach will indeed fail to solve a solvable problem. Our analysis show that the number of trajectories needed scales gracefully.

Conditional Sparse Linear Regression

Machine learning and statistics typically focus on building models that capture the vast majority of the data, possibly ignoring a small subset of data as "noise" or "outliers." By contrast, here we consider the problem of jointly identifying a significant (but perhaps small) segment of a population in which there is a highly sparse linear regression fit, together with the coefficients for the linear fit. We contend that such tasks are of interest both because the models themselves may be able to achieve better predictions in such special cases, but also because they may aid our understanding of the data. We give algorithms for such problems under the sup norm, when this unknown segment of the population is described by a k-DNF condition and the regression fit is s-sparse for constant k and s. For the variants of this problem when the regression fit is not so sparse or using expected error, we also give a preliminary algorithm and highlight the question as a challenge for future work.

PAC Quasi-automatizability of Resolution over Restricted Distributions

We consider principled alternatives to unsupervised learning in data mining by situating the learning task in the context of the subsequent analysis task. Specifically, we consider a query-answering (hypothesis-testing) task: In the combined task, we decide whether an input query formula is satisfied over a background distribution by using input examples directly, rather than invoking a two-stage process in which (i) rules over the distribution are learned by an unsupervised learning algorithm and (ii) a reasoning algorithm decides whether or not the query formula follows from the learned rules. In a previous work (2013), we observed that the learning task could satisfy numerous desirable criteria in this combined context -- effectively matching what could be achieved by agnostic learning of CNFs from partial information -- that are not known to be achievable directly. In this work, we show that likewise, there are reasoning tasks that are achievable in such a combined context that are not known to be achievable directly (and indeed, have been seriously conjectured to be impossible, cf. (Alekhnovich and Razborov, 2008)). Namely, we test for a resolution proof of the query formula of a given size in quasipolynomial time (that is, "quasi-automatizing" resolution). The learning setting we consider is a partial-information, restricted-distribution setting that generalizes learning parities over the uniform distribution from partial information, another task that is known not to be achievable directly in various models (cf. (Ben-David and Dichterman, 1998) and (Michael, 2010)).

Learning implicitly in reasoning in PAC-Semantics

We consider the problem of answering queries about formulas of propositional logic based on background knowledge partially represented explicitly as other formulas, and partially represented as partially obscured examples independently drawn from a fixed probability distribution, where the queries are answered with respect to a weaker semantics than usual -- PAC-Semantics, introduced by Valiant (2000) -- that is defined using the distribution of examples. We describe a fairly general, efficient reduction to limited versions of the decision problem for a proof system (e.g., bounded space treelike resolution, bounded degree polynomial calculus, etc.) from corresponding versions of the reasoning problem where some of the background knowledge is not explicitly given as formulas, only learnable from the examples. Crucially, we do not generate an explicit representation of the knowledge extracted from the examples, and so the "learning" of the background knowledge is only done implicitly. As a consequence, this approach can utilize formulas as background knowledge that are not perfectly valid over the distribution---essentially the analogue of agnostic learning here.

On Learning Finite-State Quantum Sources

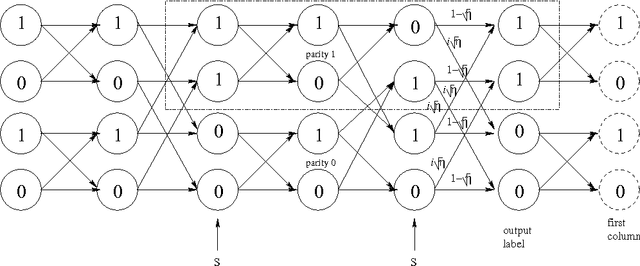
We examine the complexity of learning the distributions produced by finite-state quantum sources. We show how prior techniques for learning hidden Markov models can be adapted to the quantum generator model to find that the analogous state of affairs holds: information-theoretically, a polynomial number of samples suffice to approximately identify the distribution, but computationally, the problem is as hard as learning parities with noise, a notorious open question in computational learning theory.