Cross-channel Specific Emitter Identification and Verification via Signal Envelope

Specific emitter identification (SEI) determines which known emitter a received signal originates from, while specific emitter verification (SEV) determines whether the received signal genuinely comes from its claimed emitter. In this paper, we consider the effect of wireless fading channels on SEI and SEV. When the Rician $K$-factor varies, the resulting distribution shift induced by the channel degrades both identification and verification performance. To address this issue, we first theoretically prove that the coefficient of variation of the signal envelope is strictly monotonic with respect to the Rician $K$-factor. Motivated by this property, we propose an envelope-guided adaptive feature modulation (EAFM) identifier for SEI and an EAFM with Mahalanobis distance metric learning (EAFM-MD) verifier for SEV. Specifically, the proposed EAFM identifier adopts a dual-branch neural network to extract device-oriented features from the IQ-domain input and channel-conditioning features from the normalized signal envelope, and adaptively modulates the former via feature-wise linear modulation. Then, we extend the EAFM identifier to an EAFM-MD verifier. The device-fingerprint library is constructed by storing the feature centroid and covariance for each enrolled device, along with the within-device Mahalanobis distances of training signals. For verification, the Mahalanobis distance between the extracted test features and each stored centroid is computed using the stored covariance matrix, and the minimum distance is compared to the corresponding device threshold to make a decision. Finally, numerical results show that the proposed EAFM identifier improves cross-channel identification performance, while the proposed EAFM-MD verifier achieves superior detection performance against unknown spoofing attacks.

A Survey of Physical-layer Authentication Enhanced by Emerging Spatial Domain Technologies

This article surveys spatial-domain-enhanced Physical-layer Authentication (PLA), with Dual-polarized Antennas (DPA), Massive Multiple-Input Multiple-Output (MIMO), and Reconfigurable Intelligent Surfaces (RIS) as the primary focus. With the rapid growth of wireless deployments, authentication mechanisms face stringent requirements for high security, low overhead, and low latency. PLA offers lightweight identity verification by exploiting physical-layer characteristics. However, the effectiveness of PLA critically depends on how physical observations are constructed and validated under wireless channels. Unlike existing surveys that mainly organize PLA by authentication modality, feature source, and evaluation metrics, this work emphasizes the connection between spatial-domain enhancement mechanisms, the resulting feature representation, and the authentication procedure. We review how DPA, Massive MIMO, and RIS reshape PLA feature representation, and we summarize newly introduced security threats along with representative defense strategies. Case studies further illustrate the practical impact, such as representative detection-probability trends across Signal-to-Noise Ratio regimes and quantitative comparisons among representative schemes. Finally, we outline promising future opportunities enabled by Dynamic Metasurface Antennas, Extra-large MIMO, and spatial configuration with artificial intelligence.

Specific Multi-emitter Identification: Theoretical Limits and Low-complexity Design

Specific emitter identification (SEI) distinguishes emitters by utilizing hardware-induced signal imperfections. However, conventional SEI techniques are primarily designed for single-emitter scenarios. This poses a fundamental limitation in distributed wireless networks, where simultaneous transmissions from multiple emitters result in overlapping signals that conventional single-emitter identification methods cannot effectively handle. To overcome this limitation, we present a specific multi-emitter identification (SMEI) framework via multi-label learning, treating identification as a problem of directly decoding emitter states from overlapping signals. Theoretically, we establish performance bounds using Fano's inequality. Methodologically, the multi-label formulation reduces output dimensionality from exponential to linear scale, thereby substantially decreasing computational complexity. Additionally, we propose an improved SMEI (I-SMEI), which incorporates multi-head attention to effectively capture features in correlated signal combinations. Experimental results demonstrate that SMEI achieves high identification accuracy with a linear computational complexity. Furthermore, the proposed I-SMEI scheme significantly improves identification accuracy across various overlapping scenarios compared to the proposed SMEI and other advanced methods.

Specific multi-emitter identification via multi-label learning

Specific emitter identification leverages hardware-induced impairments to uniquely determine a specific transmitter. However, existing approaches fail to address scenarios where signals from multiple emitters overlap. In this paper, we propose a specific multi-emitter identification (SMEI) method via multi-label learning to determine multiple transmitters. Specifically, the multi-emitter fingerprint extractor is designed to mitigate the mutual interference among overlapping signals. Then, the multi-emitter decision maker is proposed to assign the all emitter identification using the previous extracted fingerprint. Experimental results demonstrate that, compared with baseline approach, the proposed SMEI scheme achieves comparable identification accuracy under various overlapping conditions, while operating at significantly lower complexity. The significance of this paper is to identify multiple emitters from overlapped signal with a low complexity.

Rethinking: Deep-learning-based Demodulation and Decoding

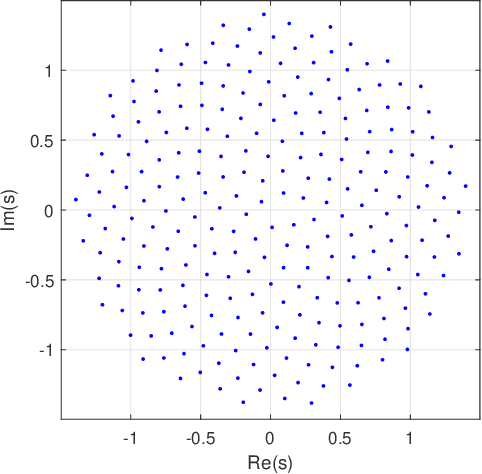
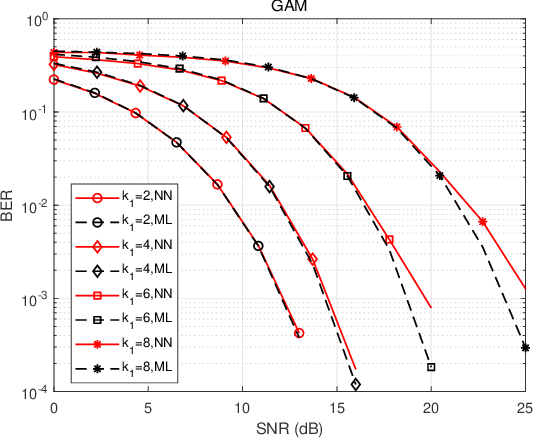
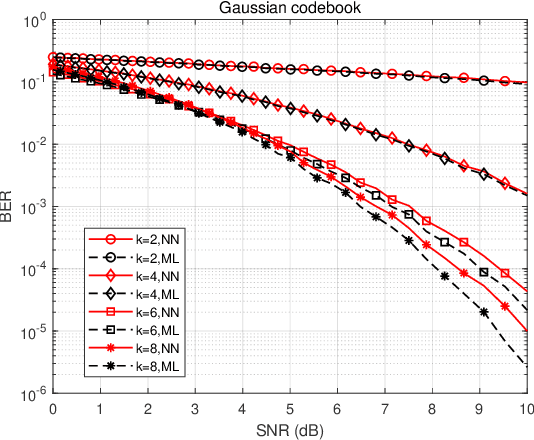
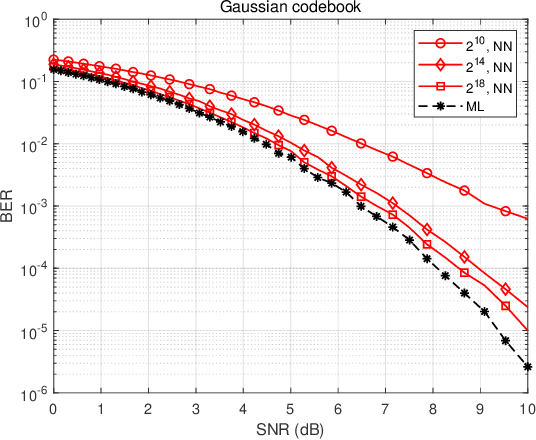
In this paper, we focus on the demodulation/decoding of the complex modulations/codes that approach the Shannon capacity. Theoretically, the maximum likelihood (ML) algorithm can achieve the optimal error performance whereas it has $\mathcal{O}(2^k)$ demodulation/decoding complexity with $k$ denoting the number of information bits. Recent progress in deep learning provides a new direction to tackle the demodulation and the decoding. The purpose of this paper is to analyze the feasibility of the neural network to demodulate/decode the complex modulations/codes close to the Shannon capacity and characterize the error performance and the complexity of the neural network. Regarding the neural network demodulator, we use the golden angle modulation (GAM), a promising modulation format that can offer the Shannon capacity approaching performance, to evaluate the demodulator. It is observed that the neural network demodulator can get a close performance to the ML-based method while it suffers from the lower complexity order in the low-order GAM. Regarding the neural network decoder, we use the Gaussian codebook, achieving the Shannon capacity, to evaluate the decoder. We also observe that the neural network decoder achieves the error performance close to the ML decoder with a much lower complexity order in the small Gaussian codebook. Limited by the current training resources, we cannot evaluate the performance of the high-order modulation and the long codeword. But, based on the results of the low-order GAM and the small Gaussian codebook, we boldly give our conjecture: the neural network demodulator/decoder is a strong candidate approach for demodulating/decoding the complex modulations/codes close to the Shannon capacity owing to the error performance of the near-ML algorithm and the lower complexity.