SpikeMatch: Semi-Supervised Learning with Temporal Dynamics of Spiking Neural Networks

Spiking neural networks (SNNs) have recently been attracting significant attention for their biological plausibility and energy efficiency, but semi-supervised learning (SSL) methods for SNN-based models remain underexplored compared to those for artificial neural networks (ANNs). In this paper, we introduce SpikeMatch, the first SSL framework for SNNs that leverages the temporal dynamics through the leakage factor of SNNs for diverse pseudo-labeling within a co-training framework. By utilizing agreement among multiple predictions from a single SNN, SpikeMatch generates reliable pseudo-labels from weakly-augmented unlabeled samples to train on strongly-augmented ones, effectively mitigating confirmation bias by capturing discriminative features with limited labels. Experiments show that SpikeMatch outperforms existing SSL methods adapted to SNN backbones across various standard benchmarks.

Design, analysis, and experimental validation of a stepped plate parametric array loudspeaker

This study investigates the design and analysis of a stepped plate parametric array loudspeaker (SPPAL) as an alternative to conventional array-based parametric loudspeakers. The SPPAL utilizes a single Langevin-type ultrasonic transducer coupled with a flexural stepped plate to generate narrow-beam audible sound via nonlinear acoustic interaction. To evaluate and optimize the performance of the SPPAL, an integrated modeling framework is developed, consisting of an approximate analytical 3D model for transducer dynamics, an equivalence ratio formulation to relate stepped plate and rigid piston behavior, and a spherical wave expansion method for nonlinear sound field simulation. The dual-resonance behavior of the transducer is optimized through multi-objective analysis to enhance low-frequency audio performance. Experimental validation includes frequency response and modal analysis of the transducer, as well as sound field measurements. The analytical methods are further verified through comparison with experimental data. Furthermore, combination resonance--an unintended structural excitation resulting from intermodulation--is identified as an inherent phenomenon in SPPAL operation. The findings offer practical guidance for the development of efficient, compact, and manufacturable parametric array loudspeakers employing plate-based flexural vibration.

An accurate measurement of parametric array using a spurious sound filter topologically equivalent to a half-wavelength resonator

Parametric arrays (PA) offer exceptional directivity and compactness compared to conventional loudspeakers, facilitating various acoustic applications. However, accurate measurement of audio signals generated by PA remains challenging due to spurious ultrasonic sounds arising from microphone nonlinearities. Existing filtering methods, including Helmholtz resonators, phononic crystals, polymer films, and grazing incidence techniques, exhibit practical constraints such as size limitations, fabrication complexity, or insufficient attenuation. To address these issues, we propose and demonstrate a novel acoustic filter based on the design of a half-wavelength resonator. The developed filter exploits the nodal plane in acoustic pressure distribution, effectively minimizing microphone exposure to targeted ultrasonic frequencies. Fabrication via stereolithography (SLA) 3D printing ensures high dimensional accuracy, which is crucial for high-frequency acoustic filters. Finite element method (FEM) simulations guided filter optimization for suppression frequencies at 40 kHz and 60 kHz, achieving high transmission loss (TL) around 60 dB. Experimental validations confirm the filter's superior performance in significantly reducing spurious acoustic signals, as reflected in frequency response, beam pattern, and propagation curve measurements. The proposed filter ensures stable and precise acoustic characterization, independent of measurement distances and incidence angles. This new approach not only improves measurement accuracy but also enhances reliability and reproducibility in parametric array research and development.

Gradient-Free Learning Based on the Kernel and the Range Space

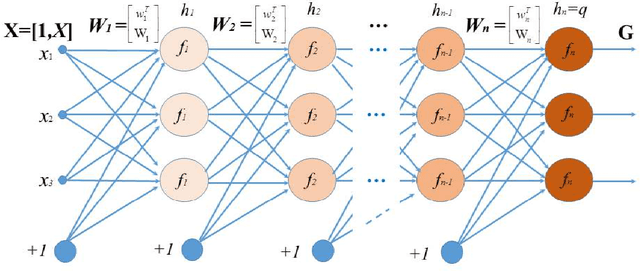
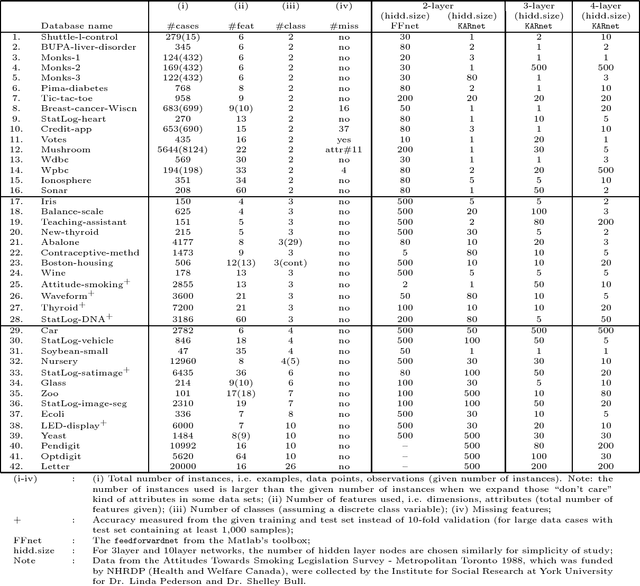
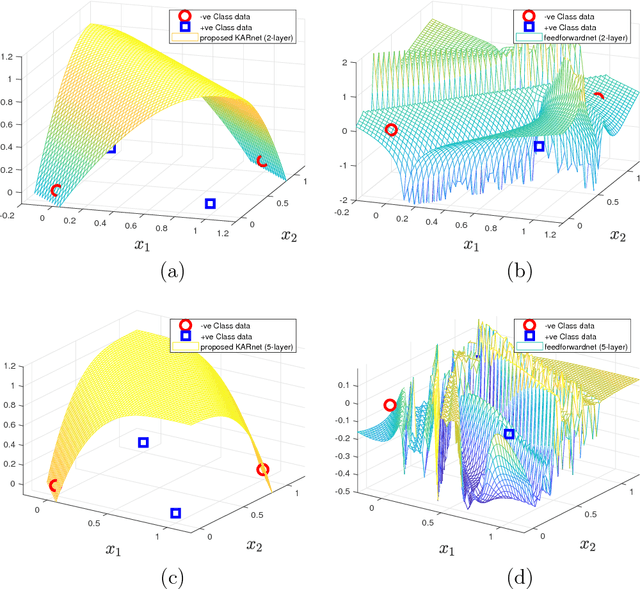
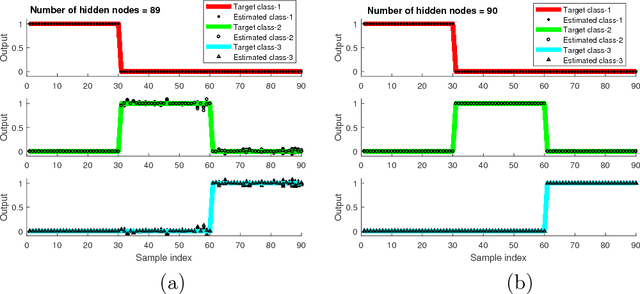
In this article, we show that solving the system of linear equations by manipulating the kernel and the range space is equivalent to solving the problem of least squares error approximation. This establishes the ground for a gradient-free learning search when the system can be expressed in the form of a linear matrix equation. When the nonlinear activation function is invertible, the learning problem of a fully-connected multilayer feedforward neural network can be easily adapted for this novel learning framework. By a series of kernel and range space manipulations, it turns out that such a network learning boils down to solving a set of cross-coupling equations. By having the weights randomly initialized, the equations can be decoupled and the network solution shows relatively good learning capability for real world data sets of small to moderate dimensions. Based on the structural information of the matrix equation, the network representation is found to be dependent on the number of data samples and the output dimension.