Parallel Correlation Clustering on Big Graphs

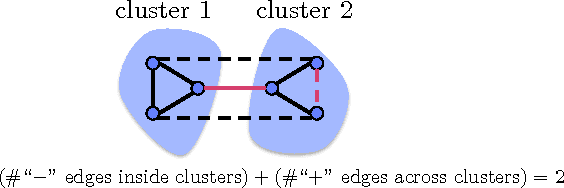
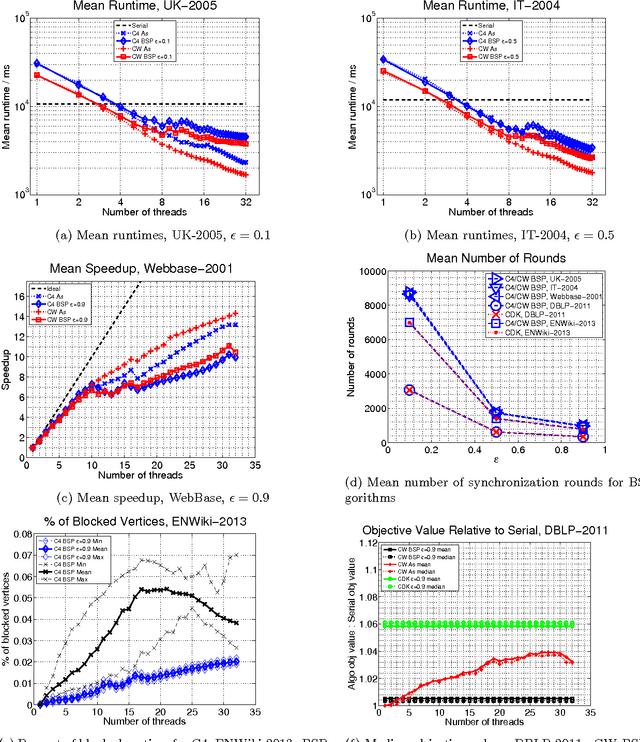
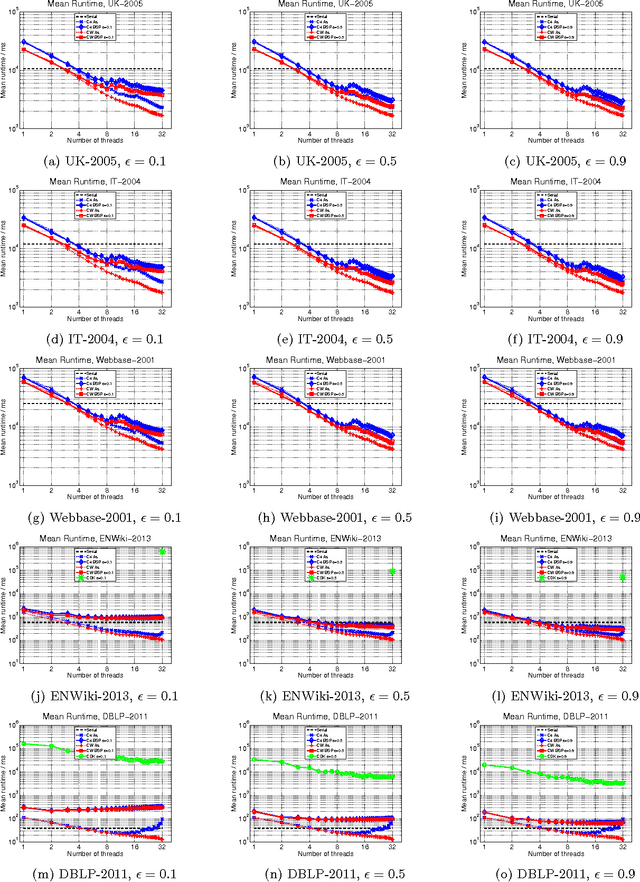
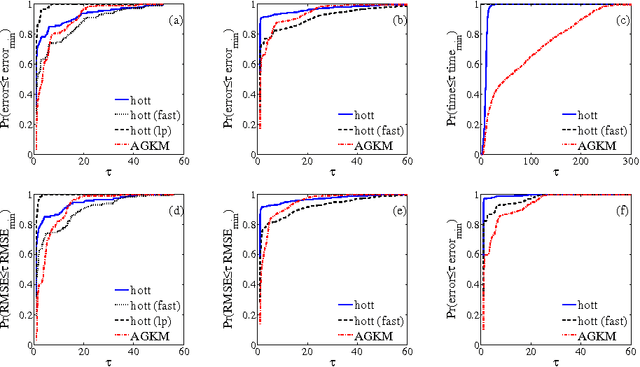
Given a similarity graph between items, correlation clustering (CC) groups similar items together and dissimilar ones apart. One of the most popular CC algorithms is KwikCluster: an algorithm that serially clusters neighborhoods of vertices, and obtains a 3-approximation ratio. Unfortunately, KwikCluster in practice requires a large number of clustering rounds, a potential bottleneck for large graphs. We present C4 and ClusterWild!, two algorithms for parallel correlation clustering that run in a polylogarithmic number of rounds and achieve nearly linear speedups, provably. C4 uses concurrency control to enforce serializability of a parallel clustering process, and guarantees a 3-approximation ratio. ClusterWild! is a coordination free algorithm that abandons consistency for the benefit of better scaling; this leads to a provably small loss in the 3-approximation ratio. We provide extensive experimental results for both algorithms, where we outperform the state of the art, both in terms of clustering accuracy and running time. We show that our algorithms can cluster billion-edge graphs in under 5 seconds on 32 cores, while achieving a 15x speedup.

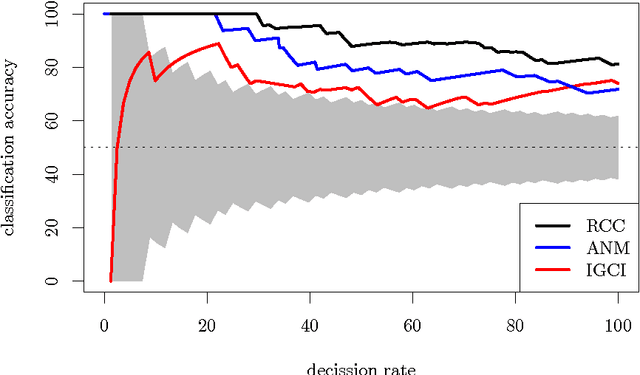
The Randomized Causation Coefficient

We are interested in learning causal relationships between pairs of random variables, purely from observational data. To effectively address this task, the state-of-the-art relies on strong assumptions regarding the mechanisms mapping causes to effects, such as invertibility or the existence of additive noise, which only hold in limited situations. On the contrary, this short paper proposes to learn how to perform causal inference directly from data, and without the need of feature engineering. In particular, we pose causality as a kernel mean embedding classification problem, where inputs are samples from arbitrary probability distributions on pairs of random variables, and labels are types of causal relationships. We validate the performance of our method on synthetic and real-world data against the state-of-the-art. Moreover, we submitted our algorithm to the ChaLearn's "Fast Causation Coefficient Challenge" competition, with which we won the fastest code prize and ranked third in the overall leaderboard.

Compressive classification and the rare eclipse problem

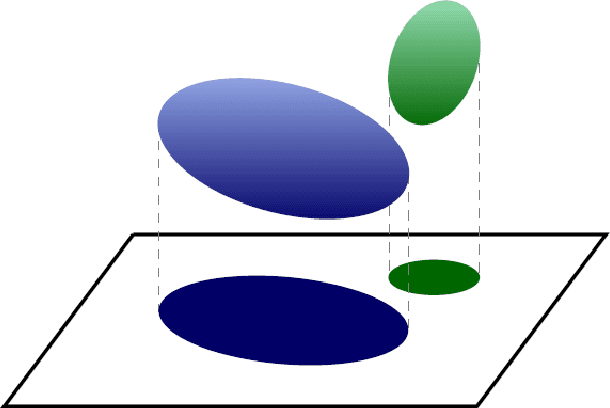
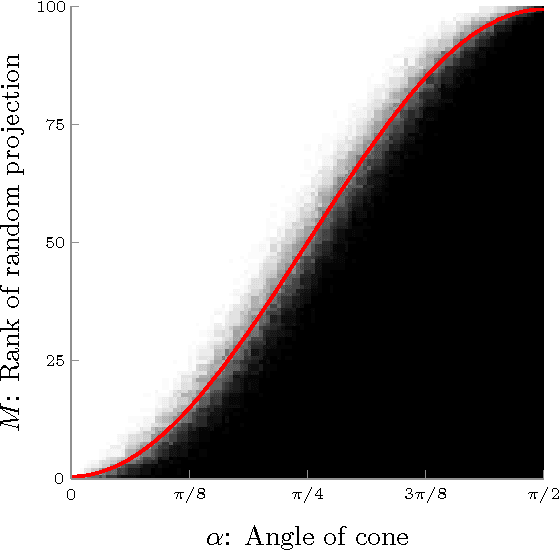
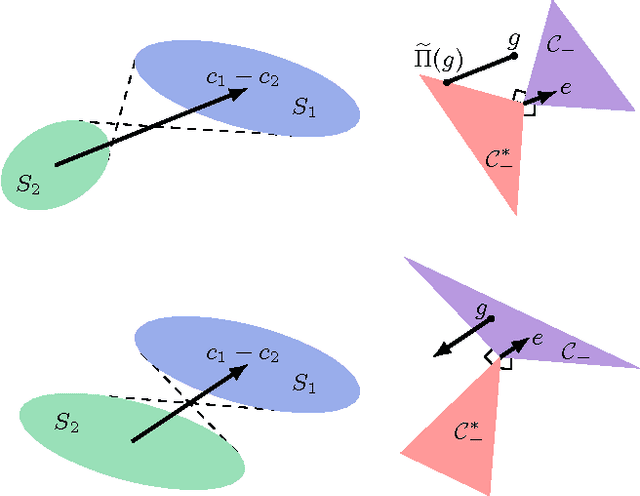
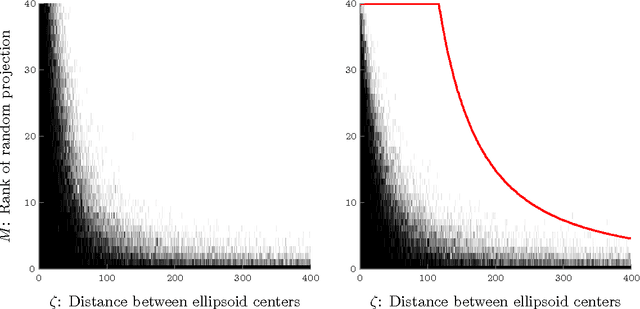
This paper addresses the fundamental question of when convex sets remain disjoint after random projection. We provide an analysis using ideas from high-dimensional convex geometry. For ellipsoids, we provide a bound in terms of the distance between these ellipsoids and simple functions of their polynomial coefficients. As an application, this theorem provides bounds for compressive classification of convex sets. Rather than assuming that the data to be classified is sparse, our results show that the data can be acquired via very few measurements yet will remain linearly separable. We demonstrate the feasibility of this approach in the context of hyperspectral imaging.

Factoring nonnegative matrices with linear programs

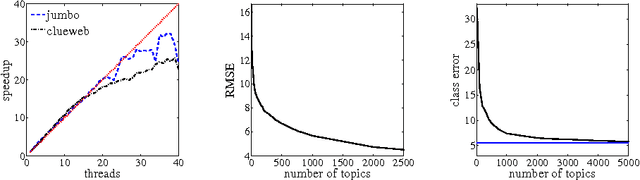
This paper describes a new approach, based on linear programming, for computing nonnegative matrix factorizations (NMFs). The key idea is a data-driven model for the factorization where the most salient features in the data are used to express the remaining features. More precisely, given a data matrix X, the algorithm identifies a matrix C such that X approximately equals CX and some linear constraints. The constraints are chosen to ensure that the matrix C selects features; these features can then be used to find a low-rank NMF of X. A theoretical analysis demonstrates that this approach has guarantees similar to those of the recent NMF algorithm of Arora et al. (2012). In contrast with this earlier work, the proposed method extends to more general noise models and leads to efficient, scalable algorithms. Experiments with synthetic and real datasets provide evidence that the new approach is also superior in practice. An optimized C++ implementation can factor a multigigabyte matrix in a matter of minutes.

Signal Recovery in Unions of Subspaces with Applications to Compressive Imaging

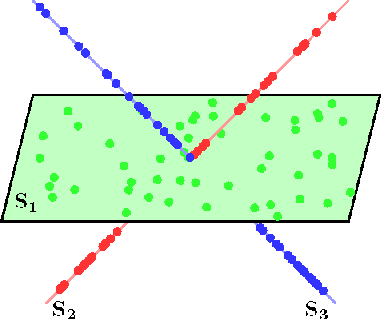
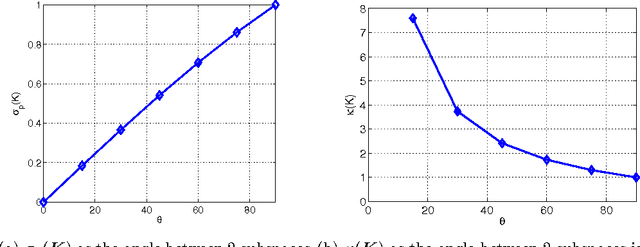
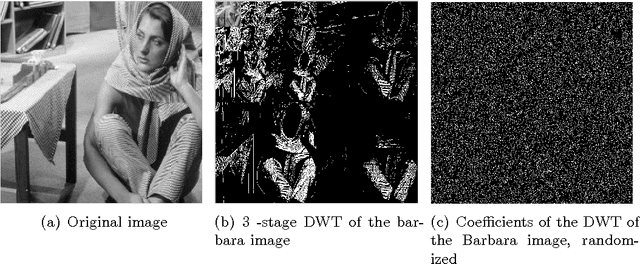
In applications ranging from communications to genetics, signals can be modeled as lying in a union of subspaces. Under this model, signal coefficients that lie in certain subspaces are active or inactive together. The potential subspaces are known in advance, but the particular set of subspaces that are active (i.e., in the signal support) must be learned from measurements. We show that exploiting knowledge of subspaces can further reduce the number of measurements required for exact signal recovery, and derive universal bounds for the number of measurements needed. The bound is universal in the sense that it only depends on the number of subspaces under consideration, and their orientation relative to each other. The particulars of the subspaces (e.g., compositions, dimensions, extents, overlaps, etc.) does not affect the results we obtain. In the process, we derive sample complexity bounds for the special case of the group lasso with overlapping groups (the latent group lasso), which is used in a variety of applications. Finally, we also show that wavelet transform coefficients of images can be modeled as lying in groups, and hence can be efficiently recovered using group lasso methods.

Query Complexity of Derivative-Free Optimization

This paper provides lower bounds on the convergence rate of Derivative Free Optimization (DFO) with noisy function evaluations, exposing a fundamental and unavoidable gap between the performance of algorithms with access to gradients and those with access to only function evaluations. However, there are situations in which DFO is unavoidable, and for such situations we propose a new DFO algorithm that is proved to be near optimal for the class of strongly convex objective functions. A distinctive feature of the algorithm is that it uses only Boolean-valued function comparisons, rather than function evaluations. This makes the algorithm useful in an even wider range of applications, such as optimization based on paired comparisons from human subjects, for example. We also show that regardless of whether DFO is based on noisy function evaluations or Boolean-valued function comparisons, the convergence rate is the same.

Beneath the valley of the noncommutative arithmetic-geometric mean inequality: conjectures, case-studies, and consequences

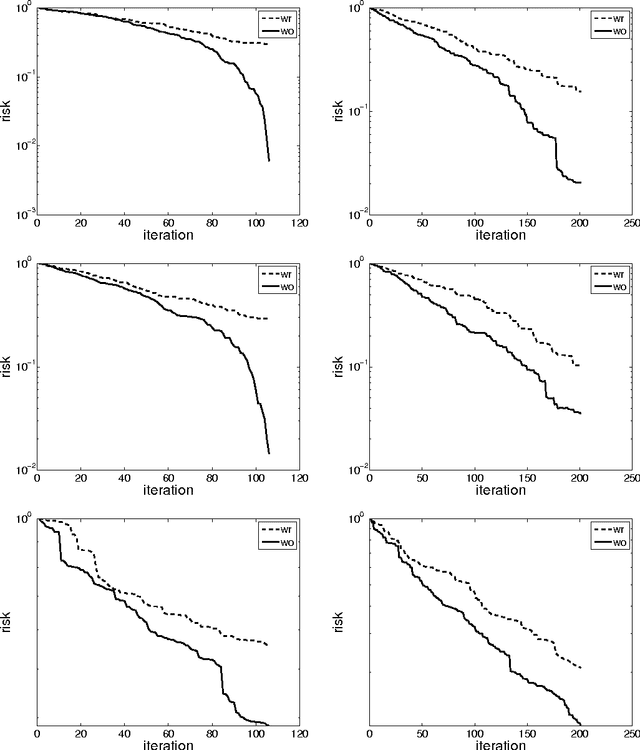
Randomized algorithms that base iteration-level decisions on samples from some pool are ubiquitous in machine learning and optimization. Examples include stochastic gradient descent and randomized coordinate descent. This paper makes progress at theoretically evaluating the difference in performance between sampling with- and without-replacement in such algorithms. Focusing on least means squares optimization, we formulate a noncommutative arithmetic-geometric mean inequality that would prove that the expected convergence rate of without-replacement sampling is faster than that of with-replacement sampling. We demonstrate that this inequality holds for many classes of random matrices and for some pathological examples as well. We provide a deterministic worst-case bound on the gap between the discrepancy between the two sampling models, and explore some of the impediments to proving this inequality in full generality. We detail the consequences of this inequality for stochastic gradient descent and the randomized Kaczmarz algorithm for solving linear systems.

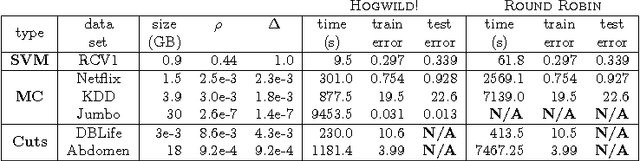
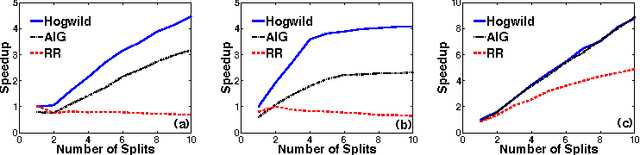
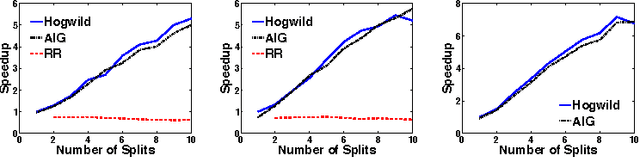
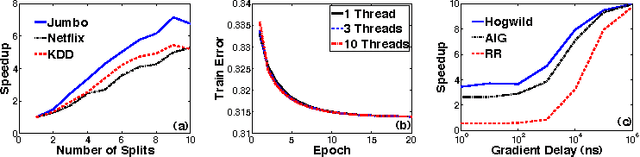
HOGWILD!: A Lock-Free Approach to Parallelizing Stochastic Gradient Descent

Stochastic Gradient Descent (SGD) is a popular algorithm that can achieve state-of-the-art performance on a variety of machine learning tasks. Several researchers have recently proposed schemes to parallelize SGD, but all require performance-destroying memory locking and synchronization. This work aims to show using novel theoretical analysis, algorithms, and implementation that SGD can be implemented without any locking. We present an update scheme called HOGWILD! which allows processors access to shared memory with the possibility of overwriting each other's work. We show that when the associated optimization problem is sparse, meaning most gradient updates only modify small parts of the decision variable, then HOGWILD! achieves a nearly optimal rate of convergence. We demonstrate experimentally that HOGWILD! outperforms alternative schemes that use locking by an order of magnitude.

Tight Measurement Bounds for Exact Recovery of Structured Sparse Signals

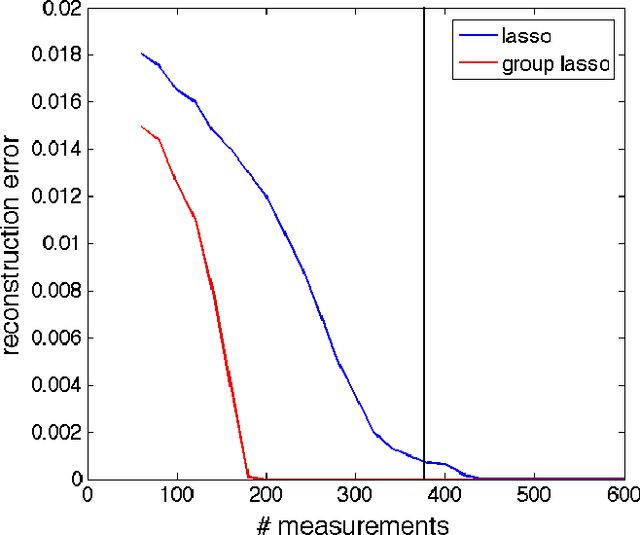
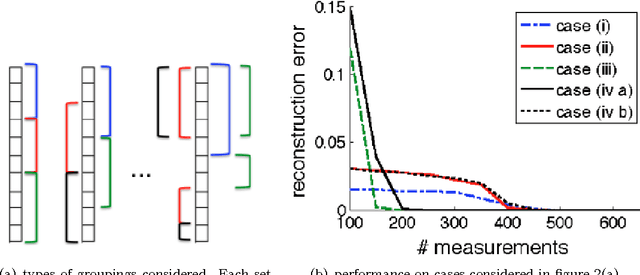
Standard compressive sensing results state that to exactly recover an s sparse signal in R^p, one requires O(s. log(p)) measurements. While this bound is extremely useful in practice, often real world signals are not only sparse, but also exhibit structure in the sparsity pattern. We focus on group-structured patterns in this paper. Under this model, groups of signal coefficients are active (or inactive) together. The groups are predefined, but the particular set of groups that are active (i.e., in the signal support) must be learned from measurements. We show that exploiting knowledge of groups can further reduce the number of measurements required for exact signal recovery, and derive universal bounds for the number of measurements needed. The bound is universal in the sense that it only depends on the number of groups under consideration, and not the particulars of the groups (e.g., compositions, sizes, extents, overlaps, etc.). Experiments show that our result holds for a variety of overlapping group configurations.

Online Identification and Tracking of Subspaces from Highly Incomplete Information

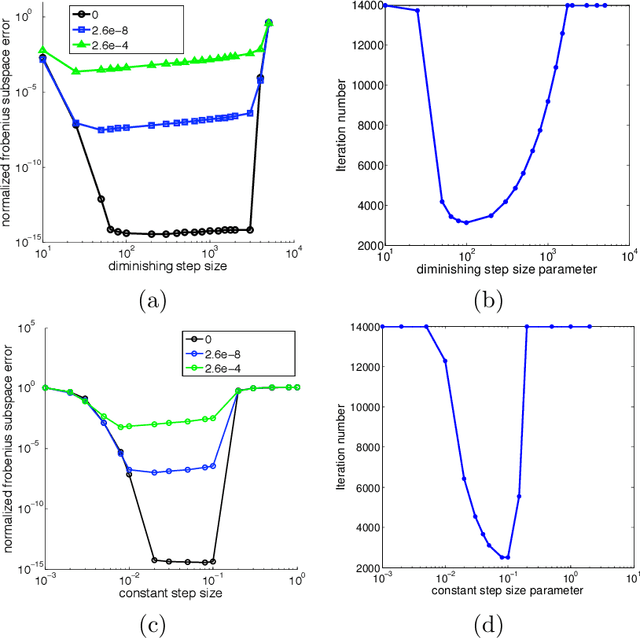
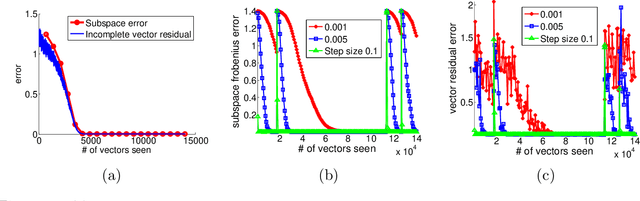
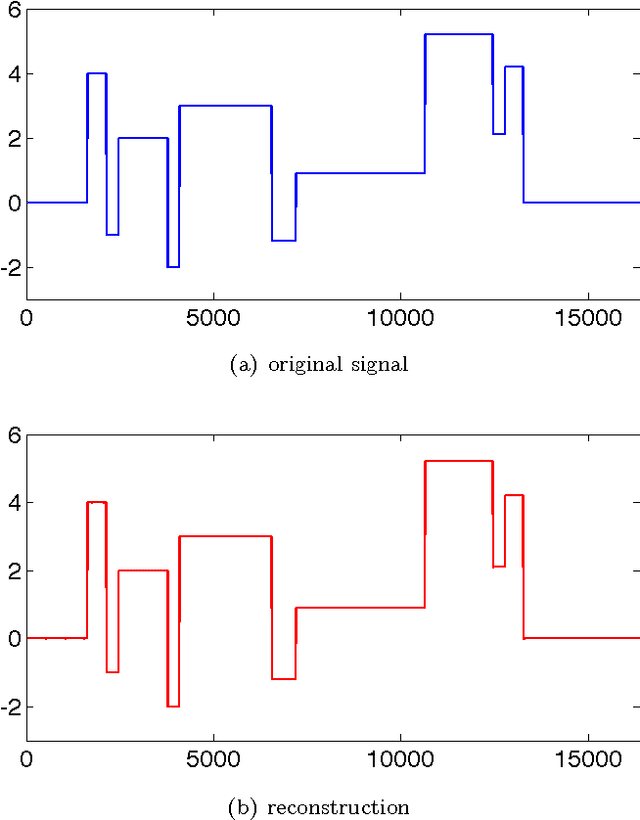
This work presents GROUSE (Grassmanian Rank-One Update Subspace Estimation), an efficient online algorithm for tracking subspaces from highly incomplete observations. GROUSE requires only basic linear algebraic manipulations at each iteration, and each subspace update can be performed in linear time in the dimension of the subspace. The algorithm is derived by analyzing incremental gradient descent on the Grassmannian manifold of subspaces. With a slight modification, GROUSE can also be used as an online incremental algorithm for the matrix completion problem of imputing missing entries of a low-rank matrix. GROUSE performs exceptionally well in practice both in tracking subspaces and as an online algorithm for matrix completion.