Variational Principles for Mirror Descent and Mirror Langevin Dynamics

Mirror descent, introduced by Nemirovski and Yudin in the 1970s, is a primal-dual convex optimization method that can be tailored to the geometry of the optimization problem at hand through the choice of a strongly convex potential function. It arises as a basic primitive in a variety of applications, including large-scale optimization, machine learning, and control. This paper proposes a variational formulation of mirror descent and of its stochastic variant, mirror Langevin dynamics. The main idea, inspired by the classic work of Brezis and Ekeland on variational principles for gradient flows, is to show that mirror descent emerges as a closed-loop solution for a certain optimal control problem, and the Bellman value function is given by the Bregman divergence between the initial condition and the global minimizer of the objective function.

A mean-field theory of lazy training in two-layer neural nets: entropic regularization and controlled McKean-Vlasov dynamics

We consider the problem of universal approximation of functions by two-layer neural nets with random weights that are "nearly Gaussian" in the sense of Kullback-Leibler divergence. This problem is motivated by recent works on lazy training, where the weight updates generated by stochastic gradient descent do not move appreciably from the i.i.d. Gaussian initialization. We first consider the mean-field limit, where the finite population of neurons in the hidden layer is replaced by a continual ensemble, and show that our problem can be phrased as global minimization of a free-energy functional on the space of probability measures over the weights. This functional trades off the $L^2$ approximation risk against the KL divergence with respect to a centered Gaussian prior. We characterize the unique global minimizer and then construct a controlled nonlinear dynamics in the space of probability measures over weights that solves a McKean--Vlasov optimal control problem. This control problem is closely related to the Schr\"odinger bridge (or entropic optimal transport) problem, and its value is proportional to the minimum of the free energy. Finally, we show that SGD in the lazy training regime (which can be ensured by jointly tuning the variance of the Gaussian prior and the entropic regularization parameter) serves as a greedy approximation to the optimal McKean--Vlasov distributional dynamics and provide quantitative guarantees on the $L^2$ approximation error.

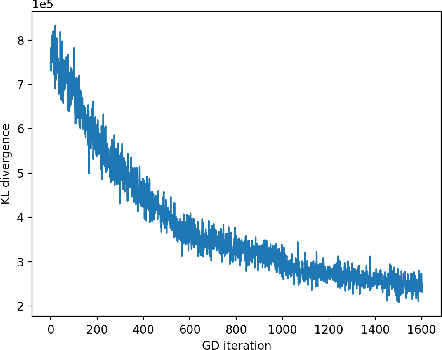
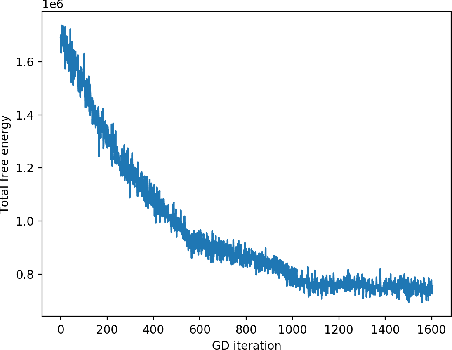
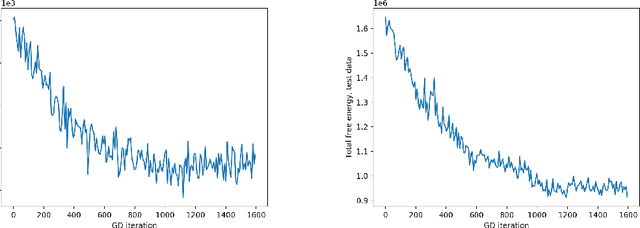
Neural Stochastic Differential Equations: Deep Latent Gaussian Models in the Diffusion Limit

In deep latent Gaussian models, the latent variable is generated by a time-inhomogeneous Markov chain, where at each time step we pass the current state through a parametric nonlinear map, such as a feedforward neural net, and add a small independent Gaussian perturbation. This work considers the diffusion limit of such models, where the number of layers tends to infinity, while the step size and the noise variance tend to zero. The limiting latent object is an It\^o diffusion process that solves a stochastic differential equation (SDE) whose drift and diffusion coefficient are implemented by neural nets. We develop a variational inference framework for these \textit{neural SDEs} via stochastic backpropagation in Wiener space, where the variational approximations to the posterior are obtained by Girsanov (mean-shift) transformation of the standard Wiener process and the computation of gradients is based on the theory of stochastic flows. This permits the use of black-box SDE solvers and automatic differentiation for end-to-end inference. Experimental results with synthetic data are provided.

Theoretical guarantees for sampling and inference in generative models with latent diffusions

We introduce and study a class of probabilistic generative models, where the latent object is a finite-dimensional diffusion process on a finite time interval and the observed variable is drawn conditionally on the terminal point of the diffusion. We make the following contributions: We provide a unified viewpoint on both sampling and variational inference in such generative models through the lens of stochastic control. We quantify the expressiveness of diffusion-based generative models. Specifically, we show that one can efficiently sample from a wide class of terminal target distributions by choosing the drift of the latent diffusion from the class of multilayer feedforward neural nets, with the accuracy of sampling measured by the Kullback-Leibler divergence to the target distribution. Finally, we present and analyze a scheme for unbiased simulation of generative models with latent diffusions and provide bounds on the variance of the resulting estimators. This scheme can be implemented as a deep generative model with a random number of layers.

Local Optimality and Generalization Guarantees for the Langevin Algorithm via Empirical Metastability

We study the detailed path-wise behavior of the discrete-time Langevin algorithm for non-convex Empirical Risk Minimization (ERM) through the lens of metastability, adopting some techniques from Berglund and Gentz (2003. For a particular local optimum of the empirical risk, with an arbitrary initialization, we show that, with high probability, at least one of the following two events will occur: (1) the Langevin trajectory ends up somewhere outside the $\varepsilon$-neighborhood of this particular optimum within a short recurrence time; (2) it enters this $\varepsilon$-neighborhood by the recurrence time and stays there until a potentially exponentially long escape time. We call this phenomenon empirical metastability. This two-timescale characterization aligns nicely with the existing literature in the following two senses. First, the effective recurrence time (i.e., number of iterations multiplied by stepsize) is dimension-independent, and resembles the convergence time of continuous-time deterministic Gradient Descent (GD). However unlike GD, the Langevin algorithm does not require strong conditions on local initialization, and has the possibility of eventually visiting all optima. Second, the scaling of the escape time is consistent with the Eyring-Kramers law, which states that the Langevin scheme will eventually visit all local minima, but it will take an exponentially long time to transit among them. We apply this path-wise concentration result in the context of statistical learning to examine local notions of generalization and optimality.