Repurposing Language Models into Embedding Models: Finding the Compute-Optimal Recipe

Text embeddings are essential for many tasks, such as document retrieval, clustering, and semantic similarity assessment. In this paper, we study how to contrastively train text embedding models in a compute-optimal fashion, given a suite of pre-trained decoder-only language models. Our innovation is an algorithm that produces optimal configurations of model sizes, data quantities, and fine-tuning methods for text-embedding models at different computational budget levels. The resulting recipe, which we obtain through extensive experiments, can be used by practitioners to make informed design choices for their embedding models. Specifically, our findings suggest that full fine-tuning and low-rank adaptation fine-tuning produce optimal models at lower and higher computational budgets respectively.

Machine-Learned Premise Selection for Lean

We introduce a machine-learning-based tool for the Lean proof assistant that suggests relevant premises for theorems being proved by a user. The design principles for the tool are (1) tight integration with the proof assistant, (2) ease of use and installation, (3) a lightweight and fast approach. For this purpose, we designed a custom version of the random forest model, trained in an online fashion. It is implemented directly in Lean, which was possible thanks to the rich and efficient metaprogramming features of Lean 4. The random forest is trained on data extracted from mathlib -- Lean's mathematics library. We experiment with various options for producing training features and labels. The advice from a trained model is accessible to the user via the suggest_premises tactic which can be called in an editor while constructing a proof interactively.

MizAR 60 for Mizar 50

As a present to Mizar on its 50th anniversary, we develop an AI/TP system that automatically proves about 60\% of the Mizar theorems in the hammer setting. We also automatically prove 75\% of the Mizar theorems when the automated provers are helped by using only the premises used in the human-written Mizar proofs. We describe the methods and large-scale experiments leading to these results. This includes in particular the E and Vampire provers, their ENIGMA and Deepire learning modifications, a number of learning-based premise selection methods, and the incremental loop that interleaves growing a corpus of millions of ATP proofs with training increasingly strong AI/TP systems on them. We also present a selection of Mizar problems that were proved automatically.

ProofNet: Autoformalizing and Formally Proving Undergraduate-Level Mathematics

We introduce ProofNet, a benchmark for autoformalization and formal proving of undergraduate-level mathematics. The ProofNet benchmarks consists of 371 examples, each consisting of a formal theorem statement in Lean 3, a natural language theorem statement, and a natural language proof. The problems are primarily drawn from popular undergraduate pure mathematics textbooks and cover topics such as real and complex analysis, linear algebra, abstract algebra, and topology. We intend for ProofNet to be a challenging benchmark that will drive progress in autoformalization and automatic theorem proving. We report baseline results on statement autoformalization via in-context learning. Moreover, we introduce two novel statement autoformalization methods: prompt retrieval and distilled backtranslation.

Online Machine Learning Techniques for Coq: A Comparison

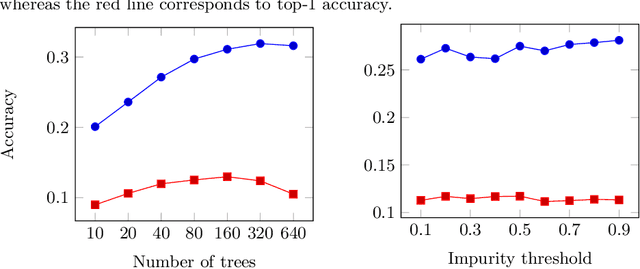
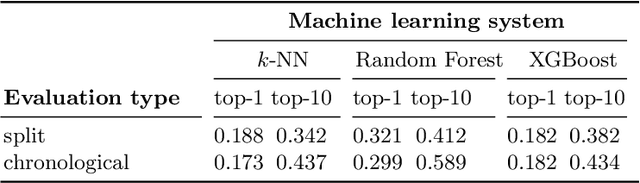
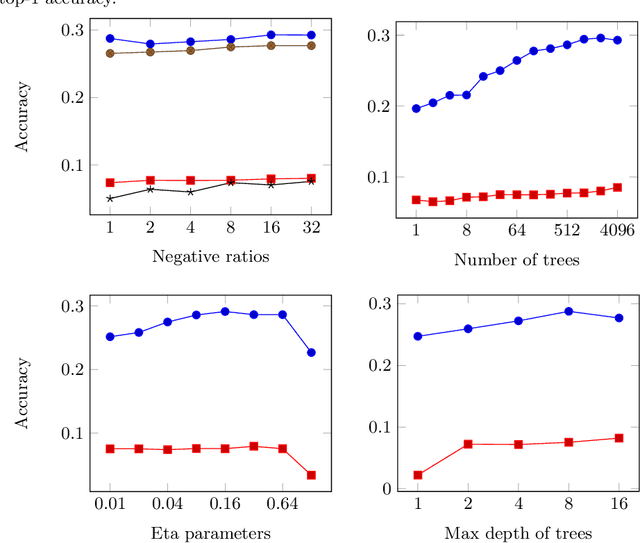
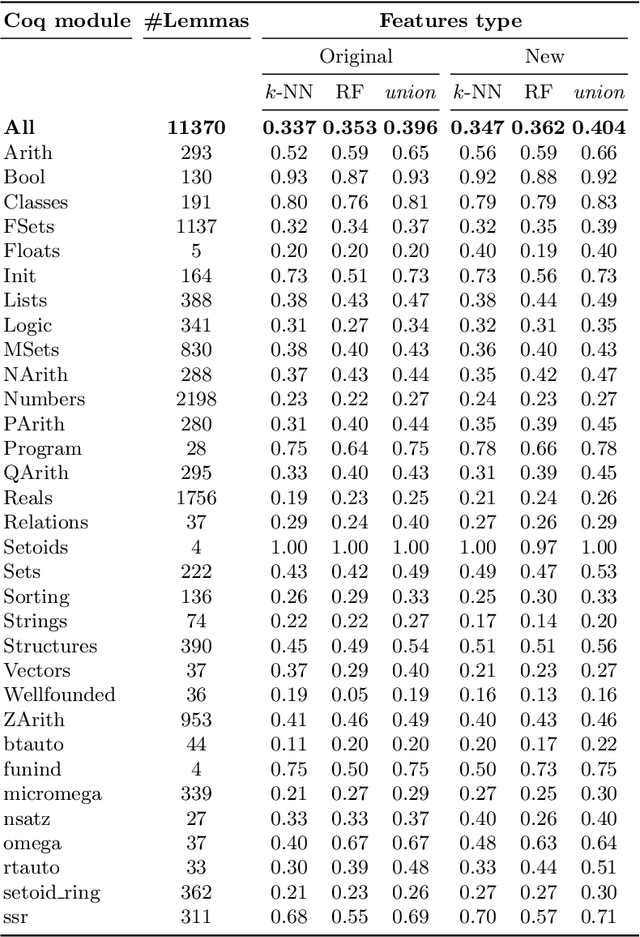
We present a comparison of several online machine learning techniques for tactical learning and proving in the Coq proof assistant. This work builds on top of Tactician, a plugin for Coq that learns from proofs written by the user to synthesize new proofs. This learning happens in an online manner -- meaning that Tactician's machine learning model is updated immediately every time the user performs a step in an interactive proof. This has important advantages compared to the more studied offline learning systems: (1) it provides the user with a seamless, interactive experience with Tactician and, (2) it takes advantage of locality of proof similarity, which means that proofs similar to the current proof are likely to be found close by. We implement two online methods, namely approximate $k$-nearest neighbors based on locality sensitive hashing forests and random decision forests. Additionally, we conduct experiments with gradient boosted trees in an offline setting using XGBoost. We compare the relative performance of Tactician using these three learning methods on Coq's standard library.

Stateful Premise Selection by Recurrent Neural Networks

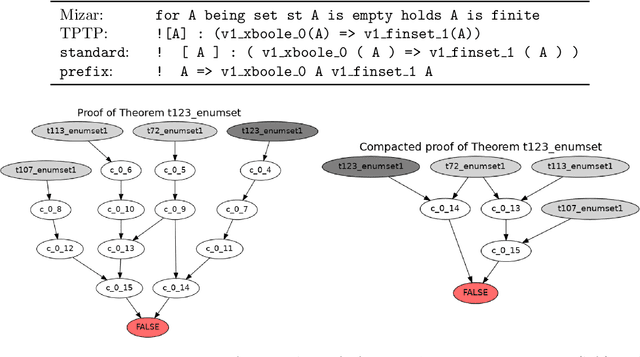
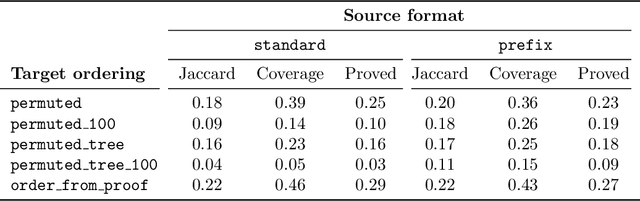
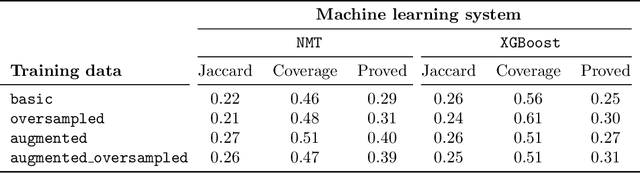
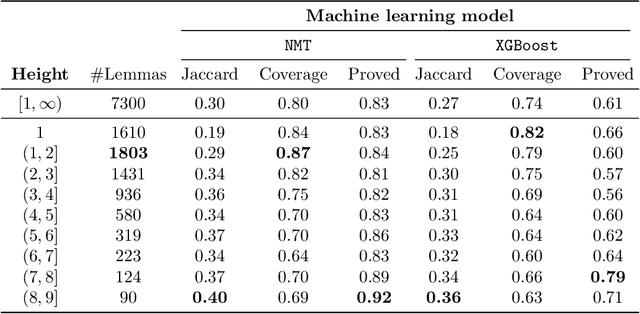
In this work, we develop a new learning-based method for selecting facts (premises) when proving new goals over large formal libraries. Unlike previous methods that choose sets of facts independently of each other by their rank, the new method uses the notion of \emph{state} that is updated each time a choice of a fact is made. Our stateful architecture is based on recurrent neural networks which have been recently very successful in stateful tasks such as language translation. The new method is combined with data augmentation techniques, evaluated in several ways on a standard large-theory benchmark, and compared to state-of-the-art premise approach based on gradient boosted trees. It is shown to perform significantly better and to solve many new problems.

ENIGMA Anonymous: Symbol-Independent Inference Guiding Machine (system description)

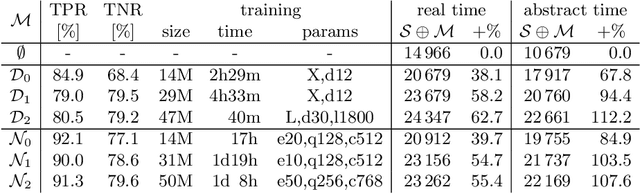
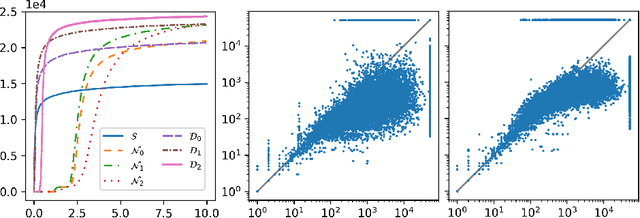
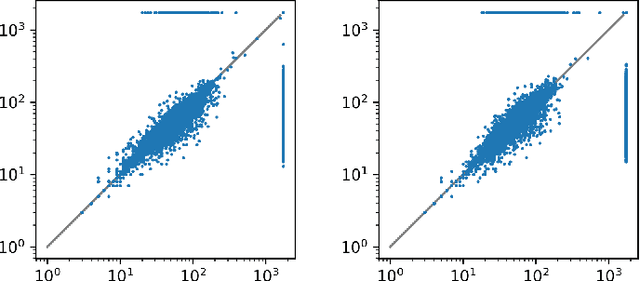
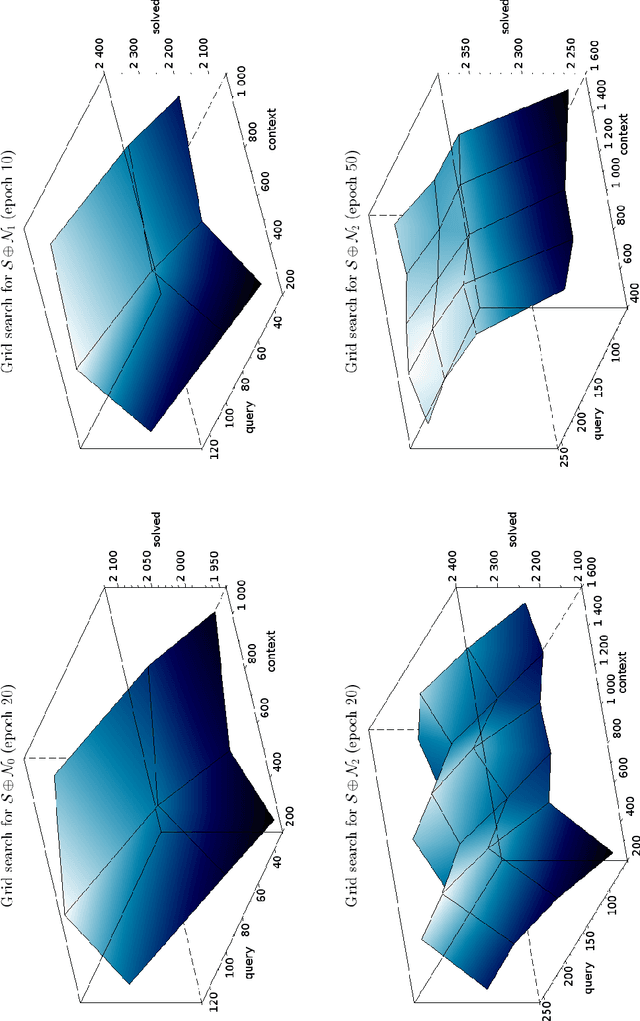
We describe an implementation of gradient boosting and neural guidance of saturation-style automated theorem provers that does not depend on consistent symbol names across problems. For the gradient-boosting guidance, we manually create abstracted features by considering arity-based encodings of formulas. For the neural guidance, we use symbol-independent graph neural networks and their embedding of the terms and clauses. The two methods are efficiently implemented in the E prover and its ENIGMA learning-guided framework and evaluated on the MPTP large-theory benchmark. Both methods are shown to achieve comparable real-time performance to state-of-the-art symbol-based methods.

Can Neural Networks Learn Symbolic Rewriting?

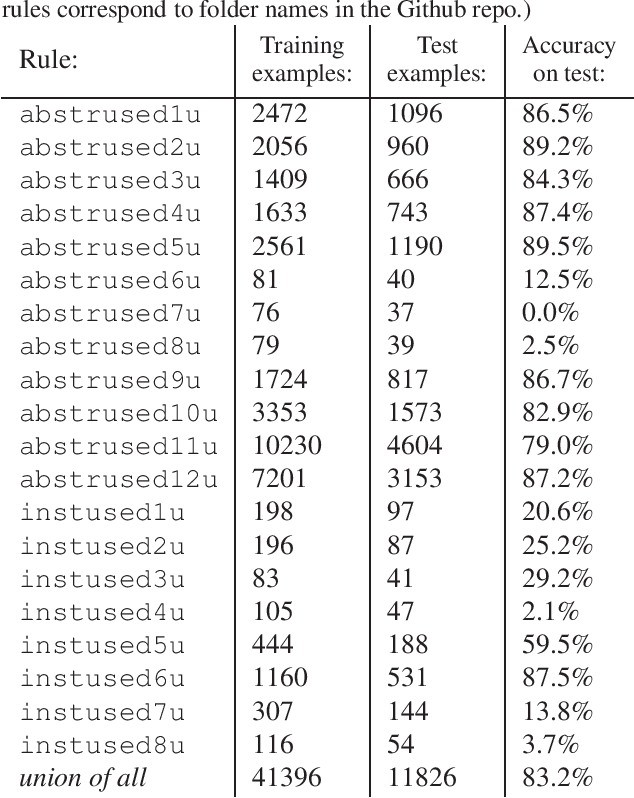
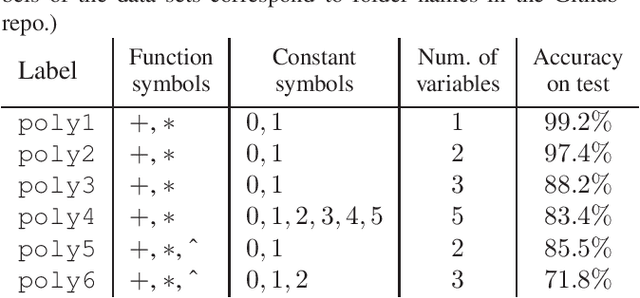
This work investigates if the current neural architectures are adequate for learning symbolic rewriting. Two kinds of data sets are proposed for this research -- one based on automated proofs and the other being a synthetic set of polynomial terms. The experiments with use of the current neural machine translation models are performed and its results are discussed. Ideas for extending this line of research are proposed and its relevance is motivated.

Guiding Theorem Proving by Recurrent Neural Networks

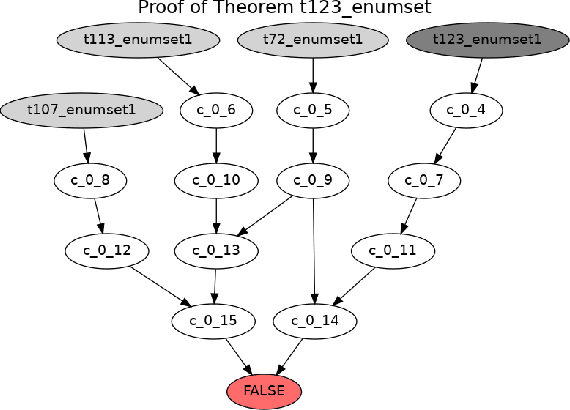
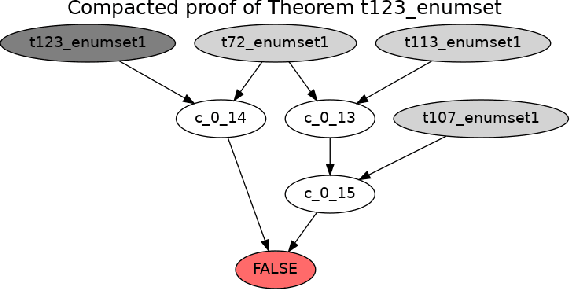
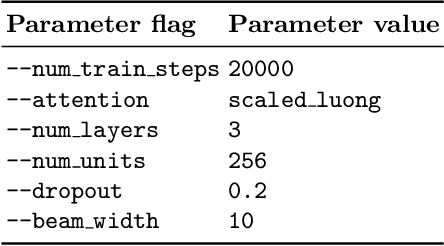
We describe two theorem proving tasks -- premise selection and internal guidance -- for which machine learning has been recently used with some success. We argue that the existing methods however do not correspond to the way how humans approach these tasks. In particular, the existing methods so far lack the notion of a state that is updated each time a choice in the reasoning process is made. To address that, we propose an analogy with tasks such as machine translation, where stateful architectures such as recurrent neural networks have been recently very successful. Then we develop and publish a series of sequence-to-sequence data sets that correspond to the theorem proving tasks using several encodings, and provide the first experimental evaluation of the performance of recurrent neural networks on such tasks.

ATPboost: Learning Premise Selection in Binary Setting with ATP Feedback

ATPboost is a system for solving sets of large-theory problems by interleaving ATP runs with state-of-the-art machine learning of premise selection from the proofs. Unlike many previous approaches that use multi-label setting, the learning is implemented as binary classification that estimates the pairwise-relevance of (theorem, premise) pairs. ATPboost uses for this the XGBoost gradient boosting algorithm, which is fast and has state-of-the-art performance on many tasks. Learning in the binary setting however requires negative examples, which is nontrivial due to many alternative proofs. We discuss and implement several solutions in the context of the ATP/ML feedback loop, and show that ATPboost with such methods significantly outperforms the k-nearest neighbors multilabel classifier.