A GREAT Architecture for Edge-Based Graph Problems Like TSP

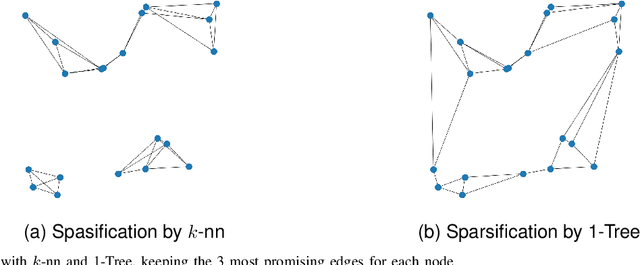
In the last years, many neural network-based approaches have been proposed to tackle combinatorial optimization problems such as routing problems. Many of these approaches are based on graph neural networks (GNNs) or related transformers, operating on the Euclidean coordinates representing the routing problems. However, GNNs are inherently not well suited to operate on dense graphs, such as in routing problems. Furthermore, models operating on Euclidean coordinates cannot be applied to non-Euclidean versions of routing problems that are often found in real-world settings. To overcome these limitations, we propose a novel GNN-related edge-based neural model called Graph Edge Attention Network (GREAT). We evaluate the performance of GREAT in the edge-classification task to predict optimal edges in the Traveling Salesman Problem (TSP). We can use such a trained GREAT model to produce sparse TSP graph instances, keeping only the edges GREAT finds promising. Compared to other, non-learning-based methods to sparsify TSP graphs, GREAT can produce very sparse graphs while keeping most of the optimal edges. Furthermore, we build a reinforcement learning-based GREAT framework which we apply to Euclidean and non-Euclidean asymmetric TSP. This framework achieves state-of-the-art results.

Less Is More -- On the Importance of Sparsification for Transformers and Graph Neural Networks for TSP

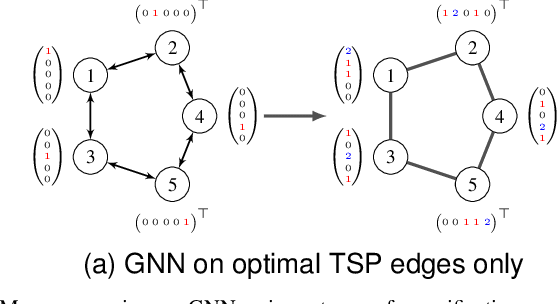
Most of the recent studies tackling routing problems like the Traveling Salesman Problem (TSP) with machine learning use a transformer or Graph Neural Network (GNN) based encoder architecture. However, many of them apply these encoders naively by allowing them to aggregate information over the whole TSP instances. We, on the other hand, propose a data preprocessing method that allows the encoders to focus on the most relevant parts of the TSP instances only. In particular, we propose graph sparsification for TSP graph representations passed to GNNs and attention masking for TSP instances passed to transformers where the masks correspond to the adjacency matrices of the sparse TSP graph representations. Furthermore, we propose ensembles of different sparsification levels allowing models to focus on the most promising parts while also allowing information flow between all nodes of a TSP instance. In the experimental studies, we show that for GNNs appropriate sparsification and ensembles of different sparsification levels lead to substantial performance increases of the overall architecture. We also design a new, state-of-the-art transformer encoder with ensembles of attention masking. These transformers increase model performance from a gap of $0.16\%$ to $0.10\%$ for TSP instances of size 100 and from $0.02\%$ to $0.00\%$ for TSP instances of size 50.

Critical Zones for Comfortable Collision Avoidance with a Leading Vehicle

This paper provides a general framework for efficiently obtaining the appropriate intervention time for collision avoidance systems to just avoid a rear-end crash. The proposed framework incorporates a driver comfort model and a vehicle model. We show that there is a relationship between driver steering manoeuvres based on acceleration and jerk, and steering angle and steering angle rate profiles. We investigate how four different vehicle models influence the time when steering needs to be initiated to avoid a rear-end collision. The models assessed were: a dynamic bicycle model (DM), a steady-state cornering model (SSCM), a kinematic model (KM) and a point mass model (PMM). We show that all models can be described by a parameter-varying linear system. We provide three algorithms for steering that use a linear system to compute the intervention time efficiently for all four vehicle models. Two of the algorithms use backward reachability simulation and one uses forward simulation. Results show that the SSCM, KM and PMM do not accurately estimate the intervention time for a certain set of vehicle conditions. Due to its fast computation time, DM with a backward reachability algorithm can be used for rapid offline safety benefit assessment, while DM with a forward simulation algorithm is better suited for online real-time usage.

Controlled Descent Training

In this work, a novel and model-based artificial neural network (ANN) training method is developed supported by optimal control theory. The method augments training labels in order to robustly guarantee training loss convergence and improve training convergence rate. Dynamic label augmentation is proposed within the framework of gradient descent training where the convergence of training loss is controlled. First, we capture the training behavior with the help of empirical Neural Tangent Kernels (NTK) and borrow tools from systems and control theory to analyze both the local and global training dynamics (e.g. stability, reachability). Second, we propose to dynamically alter the gradient descent training mechanism via fictitious labels as control inputs and an optimal state feedback policy. In this way, we enforce locally $\mathcal{H}_2$ optimal and convergent training behavior. The novel algorithm, \textit{Controlled Descent Training} (CDT), guarantees local convergence. CDT unleashes new potentials in the analysis, interpretation, and design of ANN architectures. The applicability of the method is demonstrated on standard regression and classification problems.

Deep Q-learning: a robust control approach

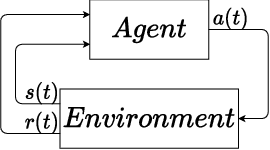
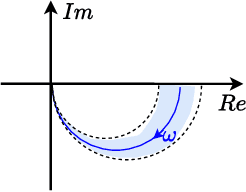
In this paper, we place deep Q-learning into a control-oriented perspective and study its learning dynamics with well-established techniques from robust control. We formulate an uncertain linear time-invariant model by means of the neural tangent kernel to describe learning. We show the instability of learning and analyze the agent's behavior in frequency-domain. Then, we ensure convergence via robust controllers acting as dynamical rewards in the loss function. We synthesize three controllers: state-feedback gain scheduling $\mathcal{H}_2$, dynamic $\mathcal{H}_\infty$, and constant gain $\mathcal{H}_\infty$ controllers. Setting up the learning agent with a control-oriented tuning methodology is more transparent and has well-established literature compared to the heuristics in reinforcement learning. In addition, our approach does not use a target network and randomized replay memory. The role of the target network is overtaken by the control input, which also exploits the temporal dependency of samples (opposed to a randomized memory buffer). Numerical simulations in different OpenAI Gym environments suggest that the $\mathcal{H}_\infty$ controlled learning performs slightly better than Double deep Q-learning.

Short-term traffic prediction using physics-aware neural networks

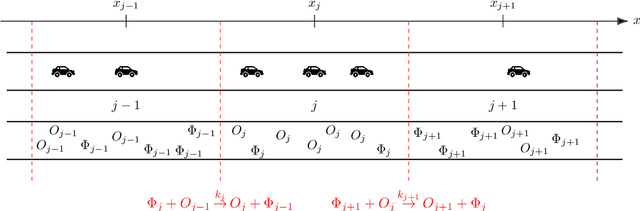
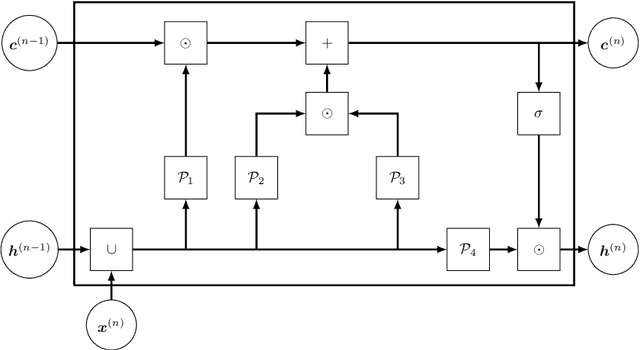
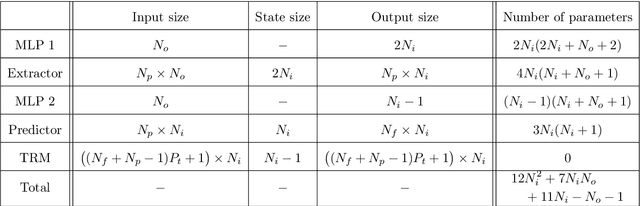
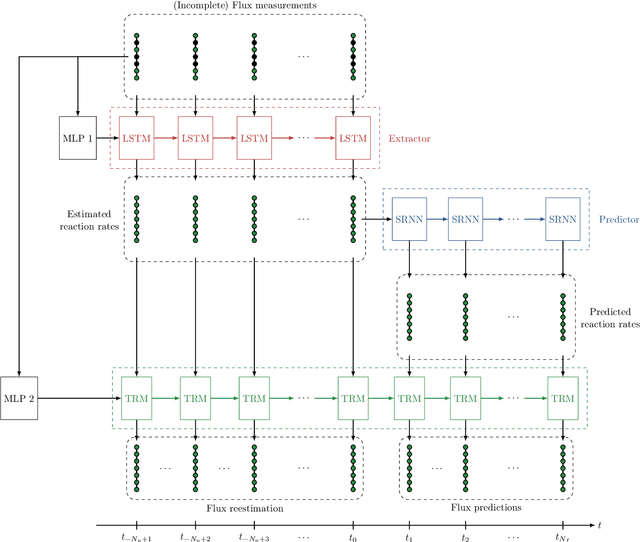
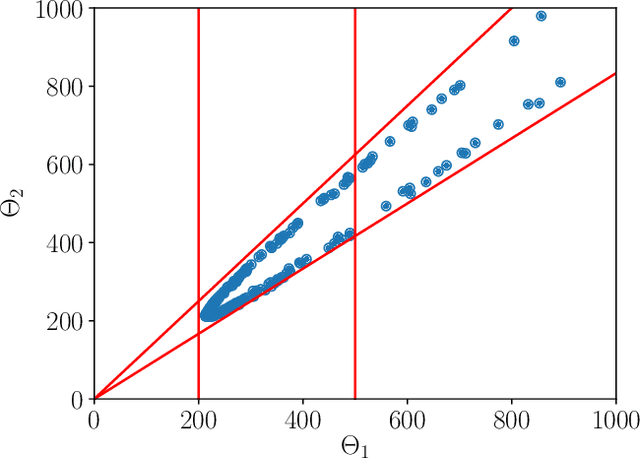
In this work, we propose an algorithm performing short-term predictions of the flux of vehicles on a stretch of road, using past measurements of the flux. This algorithm is based on a physics-aware recurrent neural network. A discretization of a macroscopic traffic flow model (using the so-called Traffic Reaction Model) is embedded in the architecture of the network and yields flux predictions based on estimated and predicted space-time dependent traffic parameters. These parameters are themselves obtained using a succession of LSTM ans simple recurrent neural networks. Besides, on top of the predictions, the algorithm yields a smoothing of its inputs which is also physically-constrained by the macroscopic traffic flow model. The algorithm is tested on raw flux measurements obtained from loop detectors.

Constrained Policy Gradient Method for Safe and Fast Reinforcement Learning: a Neural Tangent Kernel Based Approach

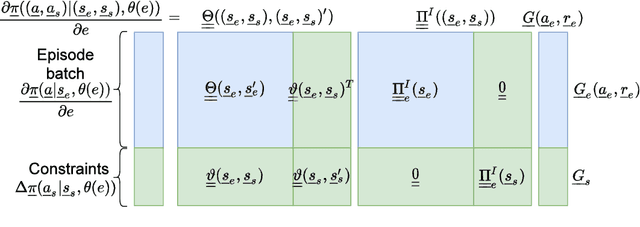
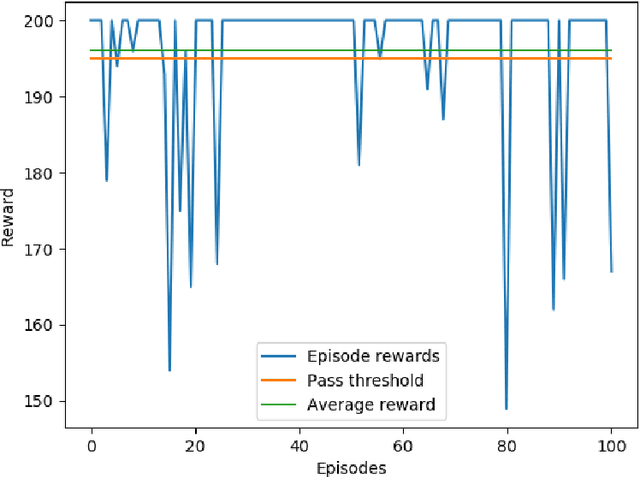
This paper presents a constrained policy gradient algorithm. We introduce constraints for safe learning with the following steps. First, learning is slowed down (lazy learning) so that the episodic policy change can be computed with the help of the policy gradient theorem and the neural tangent kernel. Then, this enables us the evaluation of the policy at arbitrary states too. In the same spirit, learning can be guided, ensuring safety via augmenting episode batches with states where the desired action probabilities are prescribed. Finally, exogenous discounted sum of future rewards (returns) can be computed at these specific state-action pairs such that the policy network satisfies constraints. Computing the returns is based on solving a system of linear equations (equality constraints) or a constrained quadratic program (inequality constraints). Simulation results suggest that adding constraints (external information) to the learning can improve learning in terms of speed and safety reasonably if constraints are appropriately selected. The efficiency of the constrained learning was demonstrated with a shallow and wide ReLU network in the Cartpole and Lunar Lander OpenAI gym environments. The main novelty of the paper is giving a practical use of the neural tangent kernel in reinforcement learning.

Parameter and density estimation from real-world traffic data: A kinetic compartmental approach

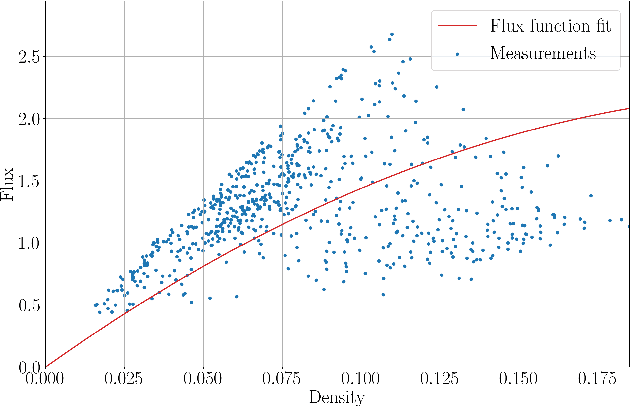
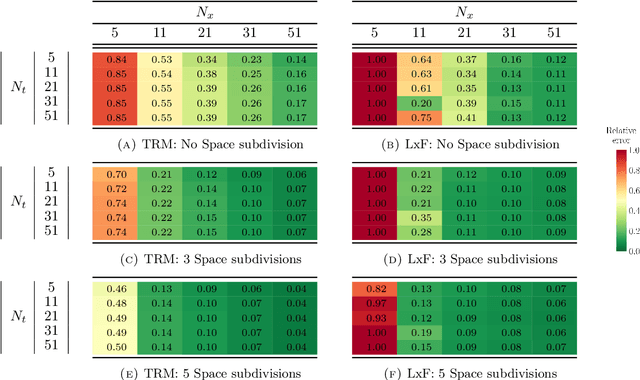
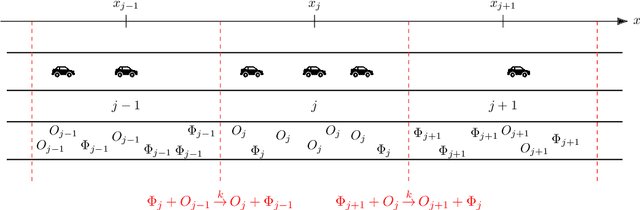
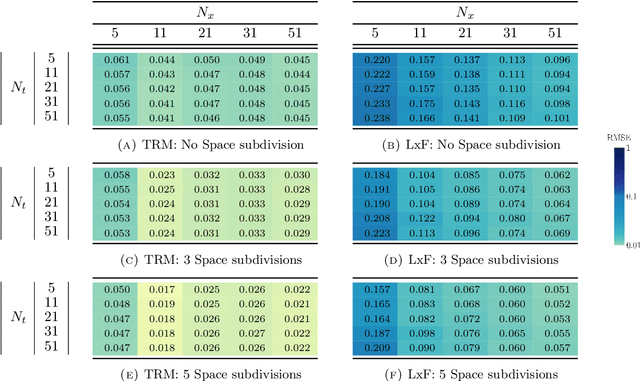
The main motivation of this work is to assess the validity of a LWR traffic flow model to model measurements obtained from trajectory data, and propose extensions of this model to improve it. A formulation for a discrete dynamical system is proposed aiming at reproducing the evolution in time of the density of vehicles along a road, as observed in the measurements. This system is formulated as a chemical reaction network where road cells are interpreted as compartments, the transfer of vehicles from one cell to the other is seen as a chemical reaction between adjacent compartment and the density of vehicles is seen as a concentration of reactant. Several degrees of flexibility on the parameters of this system, which basically consist of the reaction rates between the compartments, can be considered: a constant value or a function depending on time and/or space. Density measurements coming from trajectory data are then interpreted as observations of the states of this system at consecutive times. Optimal reaction rates for the system are then obtained by minimizing the discrepancy between the output of the system and the state measurements. This approach was tested both on simulated and real data, proved successful in recreating the complexity of traffic flows despite the assumptions on the flux-density relation.