Contextual Continuum Bandits: Static Versus Dynamic Regret

We study the contextual continuum bandits problem, where the learner sequentially receives a side information vector and has to choose an action in a convex set, minimizing a function associated to the context. The goal is to minimize all the underlying functions for the received contexts, leading to a dynamic (contextual) notion of regret, which is stronger than the standard static regret. Assuming that the objective functions are H\"older with respect to the contexts, we demonstrate that any algorithm achieving a sub-linear static regret can be extended to achieve a sub-linear dynamic regret. We further study the case of strongly convex and smooth functions when the observations are noisy. Inspired by the interior point method and employing self-concordant barriers, we propose an algorithm achieving a sub-linear dynamic regret. Lastly, we present a minimax lower bound, implying two key facts. First, no algorithm can achieve sub-linear dynamic regret over functions that are not continuous with respect to the context. Second, for strongly convex and smooth functions, the algorithm that we propose achieves, up to a logarithmic factor, the minimax optimal rate of dynamic regret as a function of the number of queries.

Gradient-free optimization of highly smooth functions: improved analysis and a new algorithm

This work studies minimization problems with zero-order noisy oracle information under the assumption that the objective function is highly smooth and possibly satisfies additional properties. We consider two kinds of zero-order projected gradient descent algorithms, which differ in the form of the gradient estimator. The first algorithm uses a gradient estimator based on randomization over the $\ell_2$ sphere due to Bach and Perchet (2016). We present an improved analysis of this algorithm on the class of highly smooth and strongly convex functions studied in the prior work, and we derive rates of convergence for two more general classes of non-convex functions. Namely, we consider highly smooth functions satisfying the Polyak-{\L}ojasiewicz condition and the class of highly smooth functions with no additional property. The second algorithm is based on randomization over the $\ell_1$ sphere, and it extends to the highly smooth setting the algorithm that was recently proposed for Lipschitz convex functions in Akhavan et al. (2022). We show that, in the case of noiseless oracle, this novel algorithm enjoys better bounds on bias and variance than the $\ell_2$ randomization and the commonly used Gaussian randomization algorithms, while in the noisy case both $\ell_1$ and $\ell_2$ algorithms benefit from similar improved theoretical guarantees. The improvements are achieved thanks to a new proof techniques based on Poincar\'e type inequalities for uniform distributions on the $\ell_1$ or $\ell_2$ spheres. The results are established under weak (almost adversarial) assumptions on the noise. Moreover, we provide minimax lower bounds proving optimality or near optimality of the obtained upper bounds in several cases.

Estimating the minimizer and the minimum value of a regression function under passive design

We propose a new method for estimating the minimizer $\boldsymbol{x}^*$ and the minimum value $f^*$ of a smooth and strongly convex regression function $f$ from the observations contaminated by random noise. Our estimator $\boldsymbol{z}_n$ of the minimizer $\boldsymbol{x}^*$ is based on a version of the projected gradient descent with the gradient estimated by a regularized local polynomial algorithm. Next, we propose a two-stage procedure for estimation of the minimum value $f^*$ of regression function $f$. At the first stage, we construct an accurate enough estimator of $\boldsymbol{x}^*$, which can be, for example, $\boldsymbol{z}_n$. At the second stage, we estimate the function value at the point obtained in the first stage using a rate optimal nonparametric procedure. We derive non-asymptotic upper bounds for the quadratic risk and optimization error of $\boldsymbol{z}_n$, and for the risk of estimating $f^*$. We establish minimax lower bounds showing that, under certain choice of parameters, the proposed algorithms achieve the minimax optimal rates of convergence on the class of smooth and strongly convex functions.

Group Meritocratic Fairness in Linear Contextual Bandits

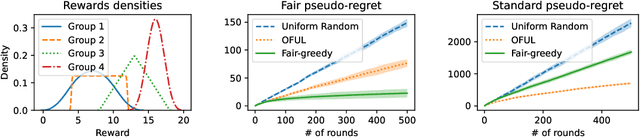
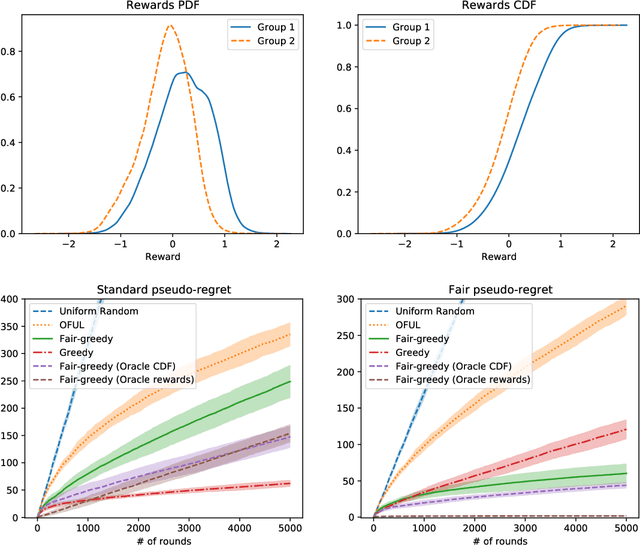
We study the linear contextual bandit problem where an agent has to select one candidate from a pool and each candidate belongs to a sensitive group. In this setting, candidates' rewards may not be directly comparable between groups, for example when the agent is an employer hiring candidates from different ethnic groups and some groups have a lower reward due to discriminatory bias and/or social injustice. We propose a notion of fairness that states that the agent's policy is fair when it selects a candidate with highest relative rank, which measures how good the reward is when compared to candidates from the same group. This is a very strong notion of fairness, since the relative rank is not directly observed by the agent and depends on the underlying reward model and on the distribution of rewards. Thus we study the problem of learning a policy which approximates a fair policy under the condition that the contexts are independent between groups and the distribution of rewards of each group is absolutely continuous. In particular, we design a greedy policy which at each round constructs a ridge regression estimator from the observed context-reward pairs, and then computes an estimate of the relative rank of each candidate using the empirical cumulative distribution function. We prove that the greedy policy achieves, after $T$ rounds, up to log factors and with high probability, a fair pseudo-regret of order $\sqrt{dT}$, where $d$ is the dimension of the context vectors. The policy also satisfies demographic parity at each round when averaged over all possible information available before the selection. We finally show with a proof of concept simulation that our policy achieves sub-linear fair pseudo-regret also in practice.

A gradient estimator via L1-randomization for online zero-order optimization with two point feedback

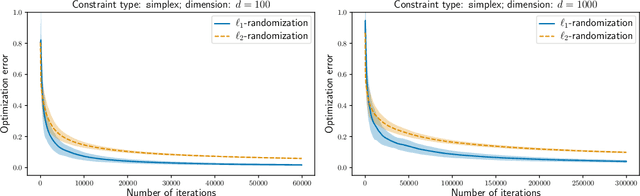
This work studies online zero-order optimization of convex and Lipschitz functions. We present a novel gradient estimator based on two function evaluation and randomization on the $\ell_1$-sphere. Considering different geometries of feasible sets and Lipschitz assumptions we analyse online mirror descent algorithm with our estimator in place of the usual gradient. We consider two types of assumptions on the noise of the zero-order oracle: canceling noise and adversarial noise. We provide an anytime and completely data-driven algorithm, which is adaptive to all parameters of the problem. In the case of canceling noise that was previously studied in the literature, our guarantees are either comparable or better than state-of-the-art bounds obtained by~\citet{duchi2015} and \citet{Shamir17} for non-adaptive algorithms. Our analysis is based on deriving a new Poincar\'e type inequality for the uniform measure on the $\ell_1$-sphere with explicit constants, which may be of independent interest.

Exploiting Higher Order Smoothness in Derivative-free Optimization and Continuous Bandits

We study the problem of zero-order optimization of a strongly convex function. The goal is to find the minimizer of the function by a sequential exploration of its values, under measurement noise. We study the impact of higher order smoothness properties of the function on the optimization error and on the cumulative regret. To solve this problem we consider a randomized approximation of the projected gradient descent algorithm. The gradient is estimated by a randomized procedure involving two function evaluations and a smoothing kernel. We derive upper bounds for this algorithm both in the constrained and unconstrained settings and prove minimax lower bounds for any sequential search method. Our results imply that the zero-order algorithm is nearly optimal in terms of sample complexity and the problem parameters. Based on this algorithm, we also propose an estimator of the minimum value of the function achieving almost sharp oracle behavior. We compare our results with the state-of-the-art, highlighting a number of key improvements.