A Physically Driven Long Short Term Memory Model for Estimating Snow Water Equivalent over the Continental United States

Snow is an essential input for various land surface models. Seasonal snow estimates are available as snow water equivalent (SWE) from process-based reanalysis products or locally from in situ measurements. While the reanalysis products are computationally expensive and available at only fixed spatial and temporal resolutions, the in situ measurements are highly localized and sparse. To address these issues and enable the analysis of the effect of a large suite of physical, morphological, and geological conditions on the presence and amount of snow, we build a Long Short-Term Memory (LSTM) network, which is able to estimate the SWE based on time series input of the various physical/meteorological factors as well static spatial/morphological factors. Specifically, this model breaks down the SWE estimation into two separate tasks: (i) a classification task that indicates the presence/absence of snow on a specific day and (ii) a regression task that indicates the height of the SWE on a specific day in the case of snow presence. The model is trained using physical/in situ SWE measurements from the SNOw TELemetry (SNOTEL) snow pillows in the western United States. We will show that trained LSTM models have a classification accuracy of $\geq 93\%$ for the presence of snow and a coefficient of correlation of $\sim 0.9$ concerning their SWE estimates. We will also demonstrate that the models can generalize both spatially and temporally to previously unseen data.

On Clustering and Embedding Mixture Manifolds using a Low Rank Neighborhood Approach

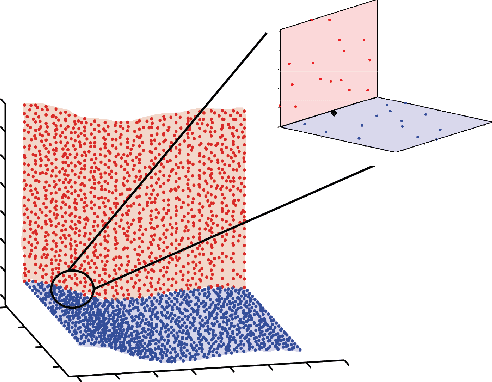
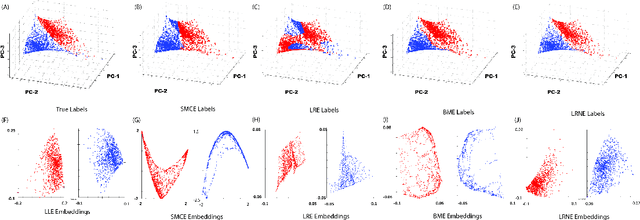
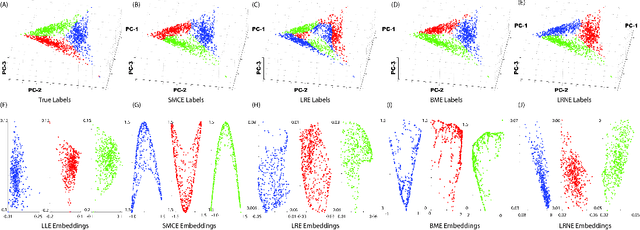
Samples from intimate (non-linear) mixtures are generally modeled as being drawn from a smooth manifold. Scenarios where the data contains multiple intimate mixtures with some constituent materials in common can be thought of as manifolds which share a boundary. Two important steps in the processing of such data are (i) to identify (cluster) the different mixture-manifolds present in the data and (ii) to eliminate the non-linearities present the data by mapping each mixture-manifold into some low-dimensional euclidean space (embedding). Manifold clustering and embedding techniques appear to be an ideal tool for this task, but the present state-of-the-art algorithms perform poorly for hyperspectral data, particularly in the embedding task. We propose a novel reconstruction-based algorithm for improved clustering and embedding of mixture-manifolds. The algorithms attempts to reconstruct each target-point as an affine combination of its nearest neighbors with an additional rank penalty on the neighborhood to ensure that only neighbors on the same manifold as the target-point are used in the reconstruction. The reconstruction matrix generated by using this technique is block-diagonal and can be used for clustering (using spectral clustering) and embedding. The improved performance of the algorithms vis-a-vis its competitors is exhibited on a variety of simulated and real mixture datasets.