Formal Model of Uncertainty for Possibilistic Rules

Given a universe of discourse X-a domain of possible outcomes-an experiment may consist of selecting one of its elements, subject to the operation of chance, or of observing the elements, subject to imprecision. A priori uncertainty about the actual result of the experiment may be quantified, representing either the likelihood of the choice of :r_X or the degree to which any such X would be suitable as a description of the outcome. The former case corresponds to a probability distribution, while the latter gives a possibility assignment on X. The study of such assignments and their properties falls within the purview of possibility theory [DP88, Y80, Z783. It, like probability theory, assigns values between 0 and 1 to express likelihoods of outcomes. Here, however, the similarity ends. Possibility theory uses the maximum and minimum functions to combine uncertainties, whereas probability theory uses the plus and times operations. This leads to very dissimilar theories in terms of analytical framework, even though they share several semantic concepts. One of the shared concepts consists of expressing quantitatively the uncertainty associated with a given distribution. In probability theory its value corresponds to the gain of information that would result from conducting an experiment and ascertaining an actual result. This gain of information can equally well be viewed as a decrease in uncertainty about the outcome of an experiment. In this case the standard measure of information, and thus uncertainty, is Shannon entropy [AD75, G77]. It enjoys several advantages-it is characterized uniquely by a few, very natural properties, and it can be conveniently used in decision processes. This application is based on the principle of maximum entropy; it has become a popular method of relating decisions to uncertainty. This paper demonstrates that an equally integrated theory can be built on the foundation of possibility theory. We first show how to define measures of in formation and uncertainty for possibility assignments. Next we construct an information-based metric on the space of all possibility distributions defined on a given domain. It allows us to capture the notion of proximity in information content among the distributions. Lastly, we show that all the above constructions can be carried out for continuous distributions-possibility assignments on arbitrary measurable domains. We consider this step very significant-finite domains of discourse are but approximations of the real-life infinite domains. If possibility theory is to represent real world situations, it must handle continuous distributions both directly and through finite approximations. In the last section we discuss a principle of maximum uncertainty for possibility distributions. We show how such a principle could be formalized as an inference rule. We also suggest it could be derived as a consequence of simple assumptions about combining information. We would like to mention that possibility assignments can be viewed as fuzzy sets and that every fuzzy set gives rise to an assignment of possibilities. This correspondence has far reaching consequences in logic and in control theory. Our treatment here is independent of any special interpretation; in particular we speak of possibility distributions and possibility measures, defining them as measurable mappings into the interval [0, 1]. Our presentation is intended as a self-contained, albeit terse summary. Topics discussed were selected with care, to demonstrate both the completeness and a certain elegance of the theory. Proofs are not included; we only offer illustrative examples.

Embedding conditional event algebras into temporal calculus of conditionals

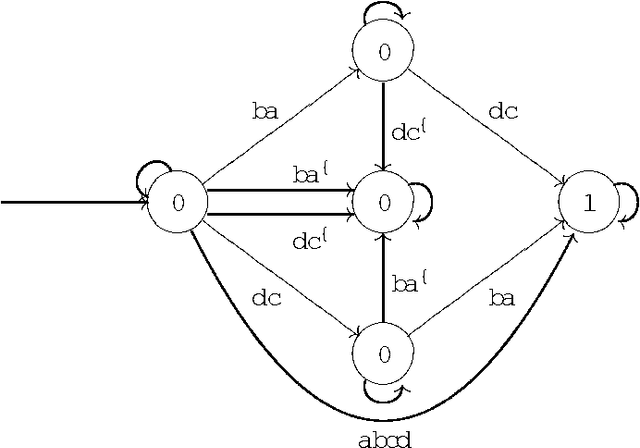
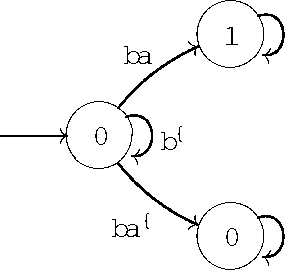
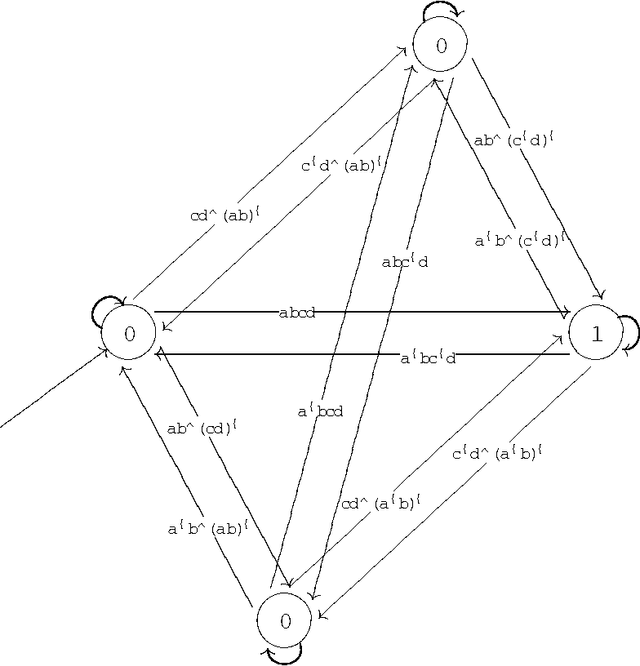
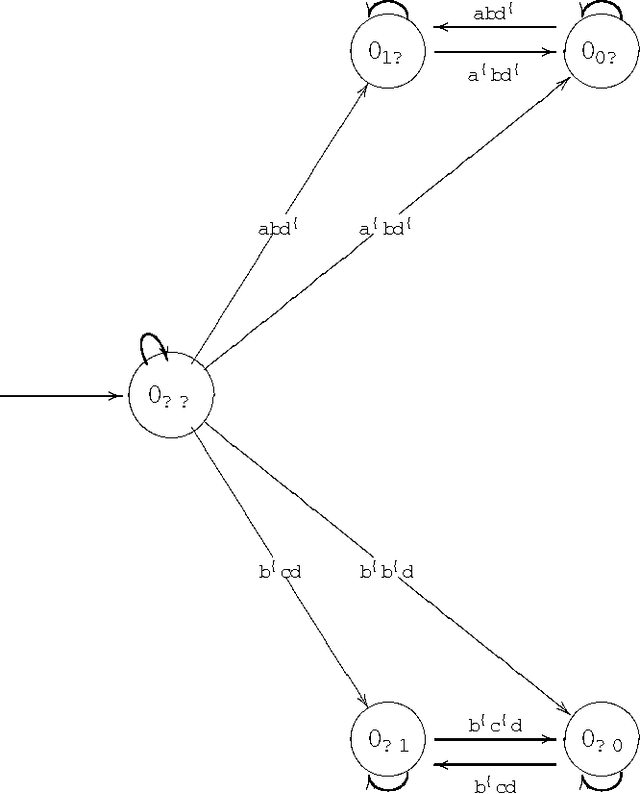
In this paper we prove that all the existing conditional event algebras embed into a three-valued extension of temporal logic of discrete past time, which the authors of this paper have proposed in anothe paper as a general model of conditional events. First of all, we discuss the descriptive incompleteness of the cea's. In this direction, we show that some important notions, like independence of conditional events, cannot be properly addressed in the framework of conditional event algebras, while they can be precisely formulated and analyzed in the temporal setting. We also demonstrate that the embeddings allow one to use Markov chain algorithms (suitable for the temporal calculus) for computing probabilities of complex conditional expressions of the embedded conditional event algebras, and that these algorithms can outperform those previously known.

The temporal calculus of conditional objects and conditional events

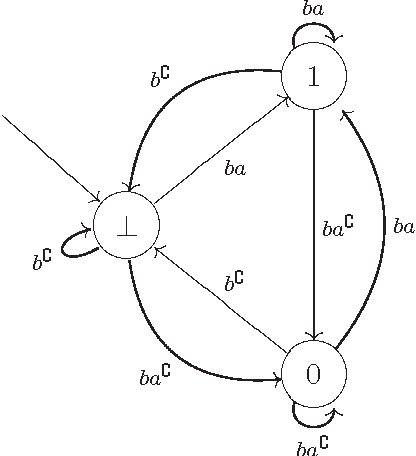
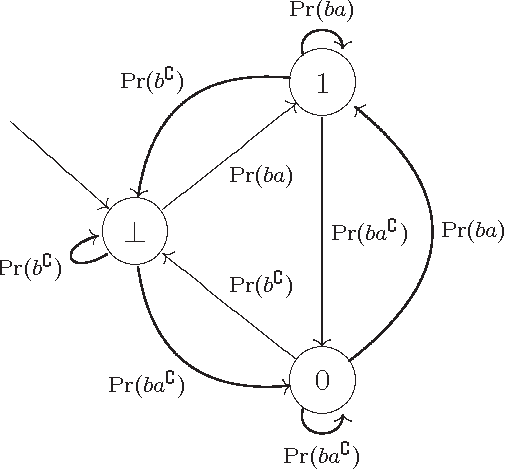
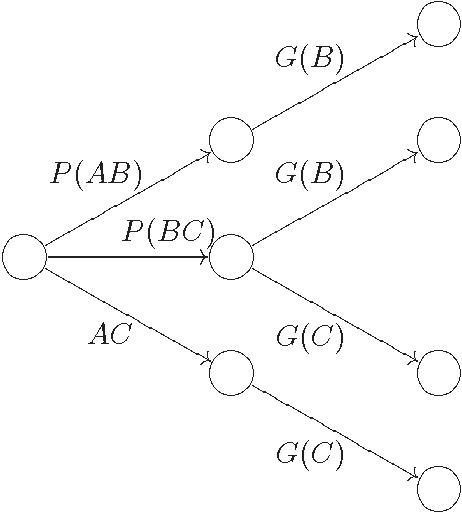
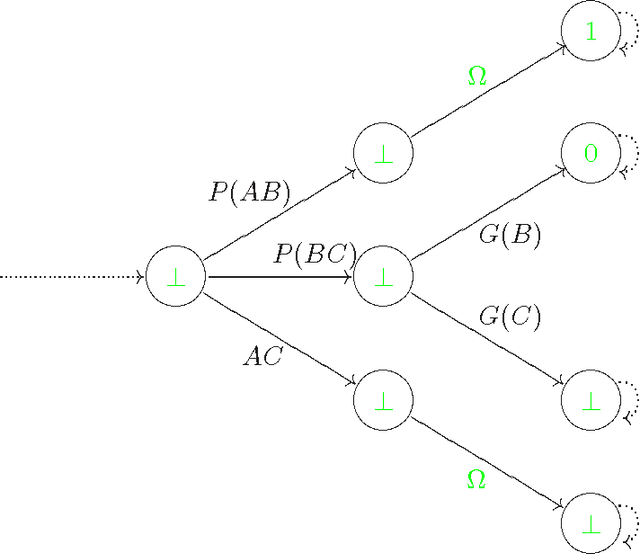
We consider the problem of defining conditional objects (a|b), which would allow one to regard the conditional probability Pr(a|b) as a probability of a well-defined event rather than as a shorthand for Pr(ab)/Pr(b). The next issue is to define boolean combinations of conditional objects, and possibly also the operator of further conditioning. These questions have been investigated at least since the times of George Boole, leading to a number of formalisms proposed for conditional objects, mostly of syntactical, proof-theoretic vein. We propose a unifying, semantical approach, in which conditional events are (projections of) Markov chains, definable in the three-valued extension of the past tense fragment of propositional linear time logic, or, equivalently, by three-valued counter-free Moore machines. Thus our conditional objects are indeed stochastic processes, one of the central notions of modern probability theory. Our model fulfills early ideas of Bruno de Finetti and, moreover, as we show in a separate paper, all the previously proposed algebras of conditional events can be isomorphically embedded in our model.