Proceedings of the Pacific Knowledge Acquisition Workshop 2004

Artificial intelligence (AI) research has evolved over the last few decades and knowledge acquisition research is at the core of AI research. PKAW-04 is one of three international knowledge acquisition workshops held in the Pacific-Rim, Canada and Europe over the last two decades. PKAW-04 has a strong emphasis on incremental knowledge acquisition, machine learning, neural nets and active mining. The proceedings contain 19 papers that were selected by the program committee among 24 submitted papers. All papers were peer reviewed by at least two reviewers. The papers in these proceedings cover the methods and tools as well as the applications related to develop expert systems or knowledge based systems.

Embedding conditional event algebras into temporal calculus of conditionals

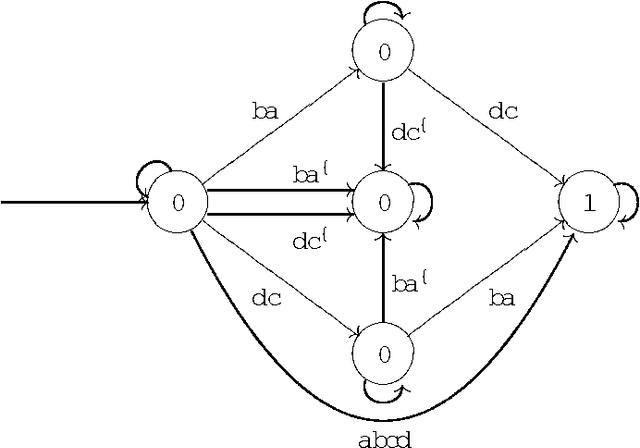
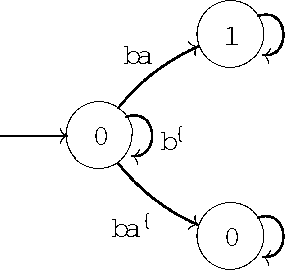
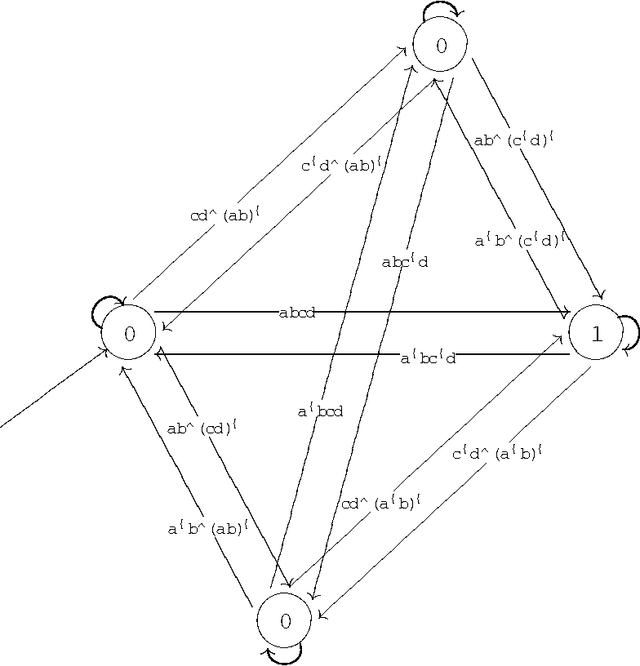
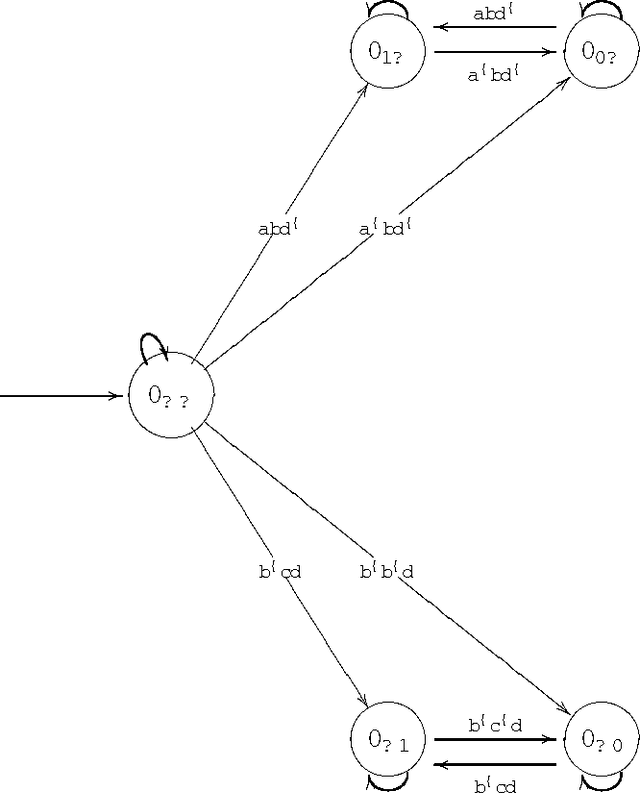
In this paper we prove that all the existing conditional event algebras embed into a three-valued extension of temporal logic of discrete past time, which the authors of this paper have proposed in anothe paper as a general model of conditional events. First of all, we discuss the descriptive incompleteness of the cea's. In this direction, we show that some important notions, like independence of conditional events, cannot be properly addressed in the framework of conditional event algebras, while they can be precisely formulated and analyzed in the temporal setting. We also demonstrate that the embeddings allow one to use Markov chain algorithms (suitable for the temporal calculus) for computing probabilities of complex conditional expressions of the embedded conditional event algebras, and that these algorithms can outperform those previously known.

The temporal calculus of conditional objects and conditional events

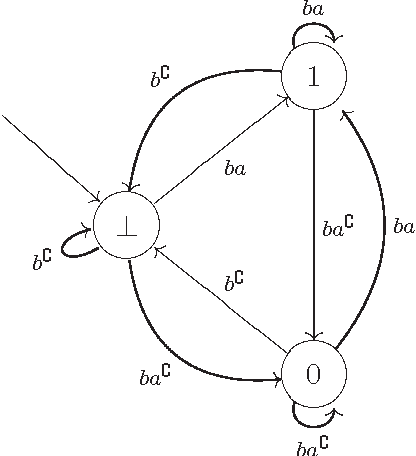
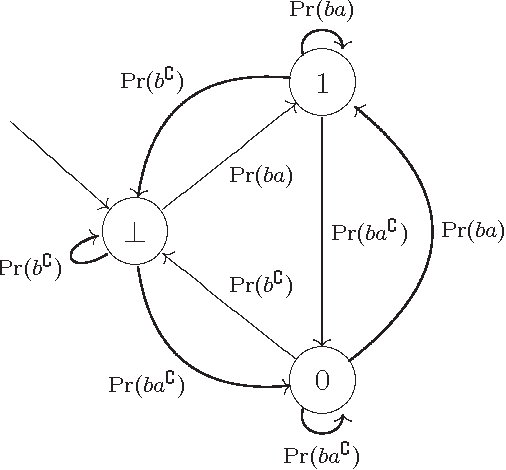
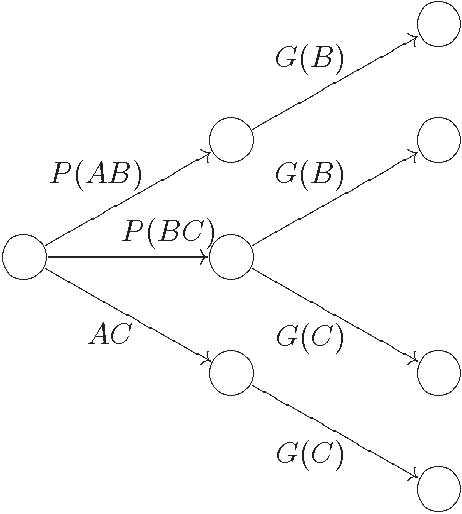
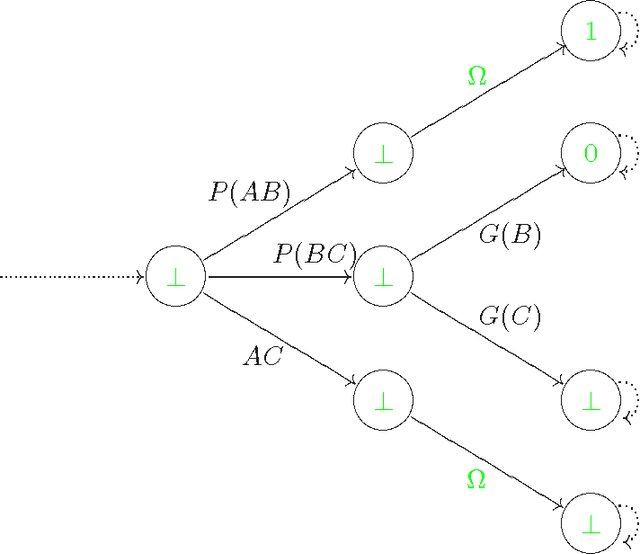
We consider the problem of defining conditional objects (a|b), which would allow one to regard the conditional probability Pr(a|b) as a probability of a well-defined event rather than as a shorthand for Pr(ab)/Pr(b). The next issue is to define boolean combinations of conditional objects, and possibly also the operator of further conditioning. These questions have been investigated at least since the times of George Boole, leading to a number of formalisms proposed for conditional objects, mostly of syntactical, proof-theoretic vein. We propose a unifying, semantical approach, in which conditional events are (projections of) Markov chains, definable in the three-valued extension of the past tense fragment of propositional linear time logic, or, equivalently, by three-valued counter-free Moore machines. Thus our conditional objects are indeed stochastic processes, one of the central notions of modern probability theory. Our model fulfills early ideas of Bruno de Finetti and, moreover, as we show in a separate paper, all the previously proposed algebras of conditional events can be isomorphically embedded in our model.