The temporal calculus of conditional objects and conditional events
Paper and Code
Oct 01, 2001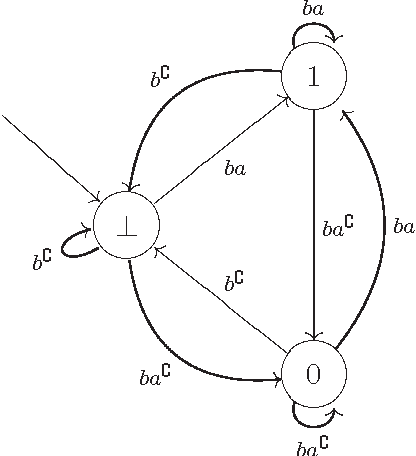
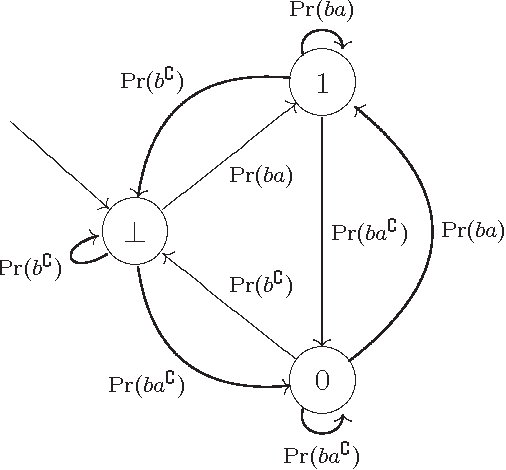
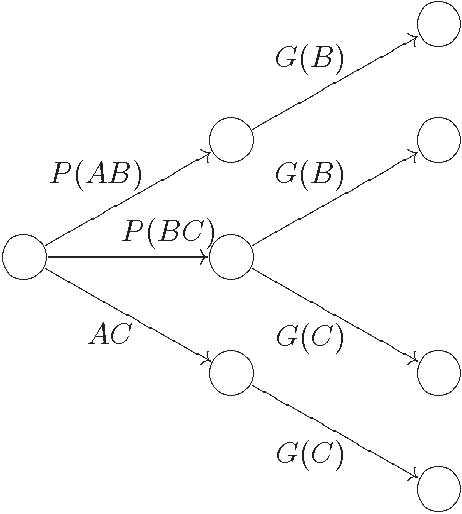
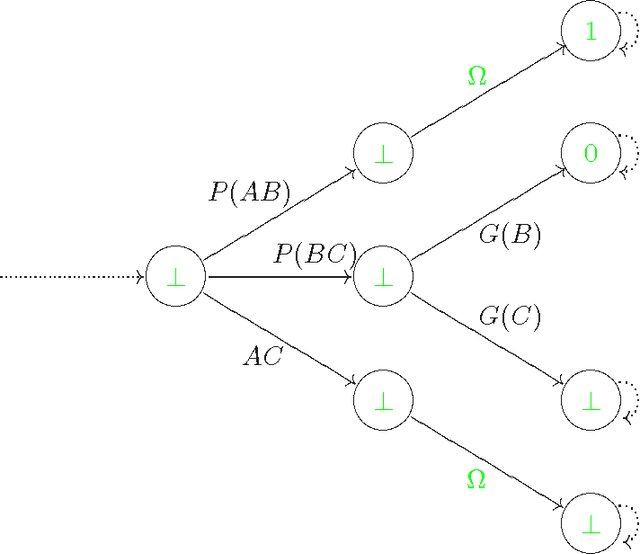
We consider the problem of defining conditional objects (a|b), which would allow one to regard the conditional probability Pr(a|b) as a probability of a well-defined event rather than as a shorthand for Pr(ab)/Pr(b). The next issue is to define boolean combinations of conditional objects, and possibly also the operator of further conditioning. These questions have been investigated at least since the times of George Boole, leading to a number of formalisms proposed for conditional objects, mostly of syntactical, proof-theoretic vein. We propose a unifying, semantical approach, in which conditional events are (projections of) Markov chains, definable in the three-valued extension of the past tense fragment of propositional linear time logic, or, equivalently, by three-valued counter-free Moore machines. Thus our conditional objects are indeed stochastic processes, one of the central notions of modern probability theory. Our model fulfills early ideas of Bruno de Finetti and, moreover, as we show in a separate paper, all the previously proposed algebras of conditional events can be isomorphically embedded in our model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge