Universal Online Optimization in Dynamic Environments via Uniclass Prediction

Recently, several universal methods have been proposed for online convex optimization which can handle convex, strongly convex and exponentially concave cost functions simultaneously. However, most of these algorithms have been designed with static regret minimization in mind, but this notion of regret may not be suitable for changing environments. To address this shortcoming, we propose a novel and intuitive framework for universal online optimization in dynamic environments. Unlike existing universal algorithms, our strategy does not rely on the construction of a set of experts and an accompanying meta-algorithm. Instead, we show that the problem of dynamic online optimization can be reduced to a uniclass prediction problem. By leaving the choice of uniclass loss function in the user's hands, they are able to control and optimize dynamic regret bounds, which in turn carry over into the original problem. To the best of our knowledge, this is the first paper proposing a universal approach with state-of-the-art dynamic regret guarantees even for general convex cost functions.

Practical Bayesian Learning of Neural Networks via Adaptive Subgradient Methods

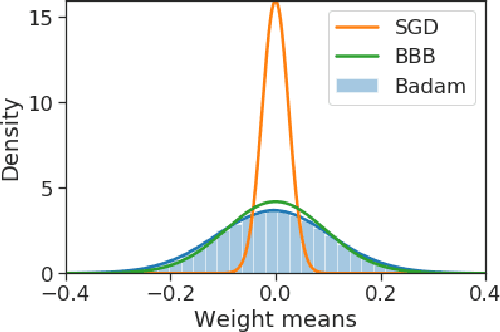
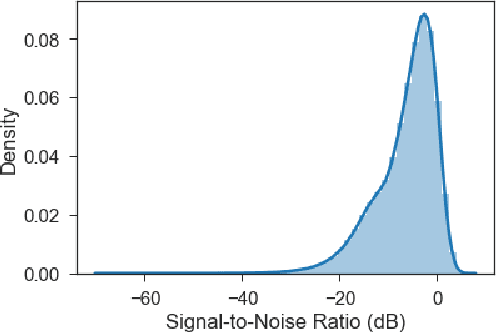
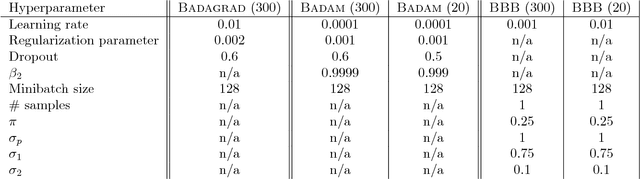
We introduce a novel framework for the estimation of the posterior distribution of the weights of a neural network, based on a new probabilistic interpretation of adaptive subgradient algorithms such as AdaGrad and Adam. Having a confidence measure of the weights allows several shortcomings of neural networks to be addressed. In particular, the robustness of the network can be improved by performing weight pruning based on signal-to-noise ratios from the weight posterior distribution. Using the MNIST dataset, we demonstrate that the empirical performance of Badam, a particular instance of our framework based on Adam, is competitive in comparison to related Bayesian approaches such as Bayes By Backprop.

A Variational Bayesian State-Space Approach to Online Passive-Aggressive Regression

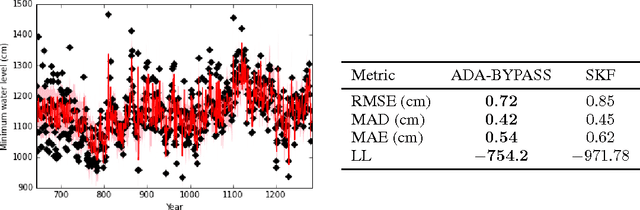
Online Passive-Aggressive (PA) learning is a class of online margin-based algorithms suitable for a wide range of real-time prediction tasks, including classification and regression. PA algorithms are formulated in terms of deterministic point-estimation problems governed by a set of user-defined hyperparameters: the approach fails to capture model/prediction uncertainty and makes their performance highly sensitive to hyperparameter configurations. In this paper, we introduce a novel PA learning framework for regression that overcomes the above limitations. We contribute a Bayesian state-space interpretation of PA regression, along with a novel online variational inference scheme, that not only produces probabilistic predictions, but also offers the benefit of automatic hyperparameter tuning. Experiments with various real-world data sets show that our approach performs significantly better than a more standard, linear Gaussian state-space model.