Bi-Level Policy Optimization with Nyström Hypergradients

The dependency of the actor on the critic in actor-critic (AC) reinforcement learning means that AC can be characterized as a bilevel optimization (BLO) problem, also called a Stackelberg game. This characterization motivates two modifications to vanilla AC algorithms. First, the critic's update should be nested to learn a best response to the actor's policy. Second, the actor should update according to a hypergradient that takes changes in the critic's behavior into account. Computing this hypergradient involves finding an inverse Hessian vector product, a process that can be numerically unstable. We thus propose a new algorithm, Bilevel Policy Optimization with Nystr\"om Hypergradients (BLPO), which uses nesting to account for the nested structure of BLO, and leverages the Nystr\"om method to compute the hypergradient. Theoretically, we prove BLPO converges to (a point that satisfies the necessary conditions for) a local strong Stackelberg equilibrium in polynomial time with high probability, assuming a linear parametrization of the critic's objective. Empirically, we demonstrate that BLPO performs on par with or better than PPO on a variety of discrete and continuous control tasks.

On the Fairness of 'Fake' Data in Legal AI

The economics of smaller budgets and larger case numbers necessitates the use of AI in legal proceedings. We examine the concept of disparate impact and how biases in the training data lead to the search for fairer AI. This paper seeks to begin the discourse on what such an implementation would actually look like with a criticism of pre-processing methods in a legal context . We outline how pre-processing is used to correct biased data and then examine the legal implications of effectively changing cases in order to achieve a fairer outcome including the black box problem and the slow encroachment on legal precedent. Finally we present recommendations on how to avoid the pitfalls of pre-processed data with methods that either modify the classifier or correct the output in the final step.

Clustering volatility regimes for dynamic trading strategies

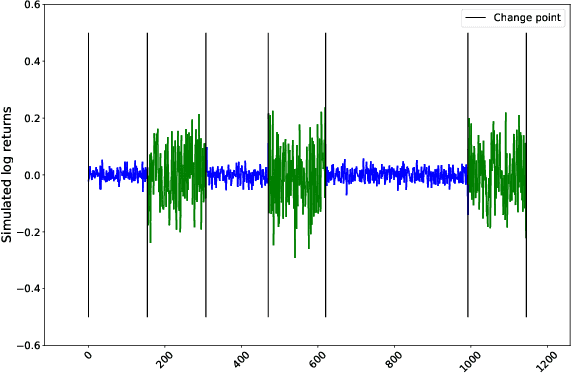
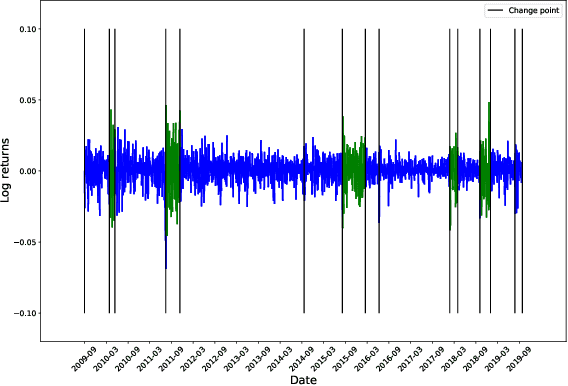
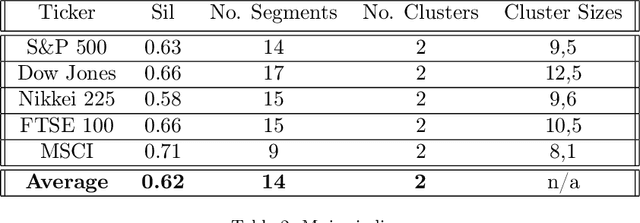
We develop a new method to find the number of volatility regimes in a non-stationary financial time series. We use change point detection to partition a time series into locally stationary segments, then estimate the distributions of each piece. The distributions are clustered into a learned number of discrete volatility regimes via an optimisation routine. Using this method, we investigate and determine a clustering structure for indices, large cap equities and exchange-traded funds. Finally, we create and validate a dynamic portfolio allocation strategy that learns the optimal match between the current distribution of a time series with its past regimes, thereby making online risk-avoidance decisions in the present.