Axiomatic Explainer Globalness via Optimal Transport

Explainability methods are often challenging to evaluate and compare. With a multitude of explainers available, practitioners must often compare and select explainers based on quantitative evaluation metrics. One particular differentiator between explainers is the diversity of explanations for a given dataset; i.e. whether all explanations are identical, unique and uniformly distributed, or somewhere between these two extremes. In this work, we define a complexity measure for explainers, globalness, which enables deeper understanding of the distribution of explanations produced by feature attribution and feature selection methods for a given dataset. We establish the axiomatic properties that any such measure should possess and prove that our proposed measure, Wasserstein Globalness, meets these criteria. We validate the utility of Wasserstein Globalness using image, tabular, and synthetic datasets, empirically showing that it both facilitates meaningful comparison between explainers and improves the selection process for explainability methods.

SmoothHess: ReLU Network Feature Interactions via Stein's Lemma

Several recent methods for interpretability model feature interactions by looking at the Hessian of a neural network. This poses a challenge for ReLU networks, which are piecewise-linear and thus have a zero Hessian almost everywhere. We propose SmoothHess, a method of estimating second-order interactions through Stein's Lemma. In particular, we estimate the Hessian of the network convolved with a Gaussian through an efficient sampling algorithm, requiring only network gradient calls. SmoothHess is applied post-hoc, requires no modifications to the ReLU network architecture, and the extent of smoothing can be controlled explicitly. We provide a non-asymptotic bound on the sample complexity of our estimation procedure. We validate the superior ability of SmoothHess to capture interactions on benchmark datasets and a real-world medical spirometry dataset.

Explanations of Black-Box Models based on Directional Feature Interactions

As machine learning algorithms are deployed ubiquitously to a variety of domains, it is imperative to make these often black-box models transparent. Several recent works explain black-box models by capturing the most influential features for prediction per instance; such explanation methods are univariate, as they characterize importance per feature. We extend univariate explanation to a higher-order; this enhances explainability, as bivariate methods can capture feature interactions in black-box models, represented as a directed graph. Analyzing this graph enables us to discover groups of features that are equally important (i.e., interchangeable), while the notion of directionality allows us to identify the most influential features. We apply our bivariate method on Shapley value explanations, and experimentally demonstrate the ability of directional explanations to discover feature interactions. We show the superiority of our method against state-of-the-art on CIFAR10, IMDB, Census, Divorce, Drug, and gene data.

Geometry of Score Based Generative Models

In this work, we look at Score-based generative models (also called diffusion generative models) from a geometric perspective. From a new view point, we prove that both the forward and backward process of adding noise and generating from noise are Wasserstein gradient flow in the space of probability measures. We are the first to prove this connection. Our understanding of Score-based (and Diffusion) generative models have matured and become more complete by drawing ideas from different fields like Bayesian inference, control theory, stochastic differential equation and Schrodinger bridge. However, many open questions and challenges remain. One problem, for example, is how to decrease the sampling time? We demonstrate that looking from geometric perspective enables us to answer many of these questions and provide new interpretations to some known results. Furthermore, geometric perspective enables us to devise an intuitive geometric solution to the problem of faster sampling. By augmenting traditional score-based generative models with a projection step, we show that we can generate high quality images with significantly fewer sampling-steps.

Divide and Compose with Score Based Generative Models

While score based generative models, or diffusion models, have found success in image synthesis, they are often coupled with text data or image label to be able to manipulate and conditionally generate images. Even though manipulation of images by changing the text prompt is possible, our understanding of the text embedding and our ability to modify it to edit images is quite limited. Towards the direction of having more control over image manipulation and conditional generation, we propose to learn image components in an unsupervised manner so that we can compose those components to generate and manipulate images in informed manner. Taking inspiration from energy based models, we interpret different score components as the gradient of different energy functions. We show how score based learning allows us to learn interesting components and we can visualize them through generation. We also show how this novel decomposition allows us to compose, generate and modify images in interesting ways akin to dreaming. We make our code available at https://github.com/sandeshgh/Score-based-disentanglement

Inv-SENnet: Invariant Self Expression Network for clustering under biased data

Subspace clustering algorithms are used for understanding the cluster structure that explains the dataset well. These methods are extensively used for data-exploration tasks in various areas of Natural Sciences. However, most of these methods fail to handle unwanted biases in datasets. For datasets where a data sample represents multiple attributes, naively applying any clustering approach can result in undesired output. To this end, we propose a novel framework for jointly removing unwanted attributes (biases) while learning to cluster data points in individual subspaces. Assuming we have information about the bias, we regularize the clustering method by adversarially learning to minimize the mutual information between the data and the unwanted attributes. Our experimental result on synthetic and real-world datasets demonstrate the effectiveness of our approach.

Explanation Uncertainty with Decision Boundary Awareness

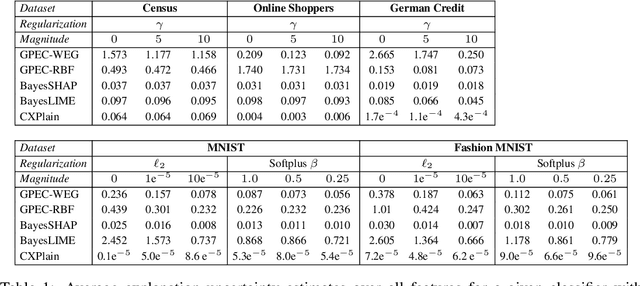
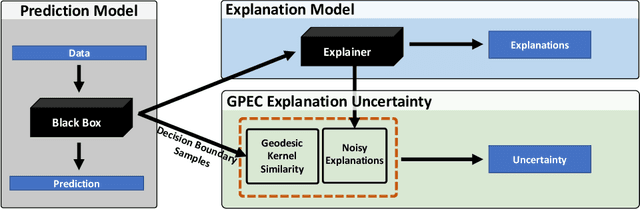
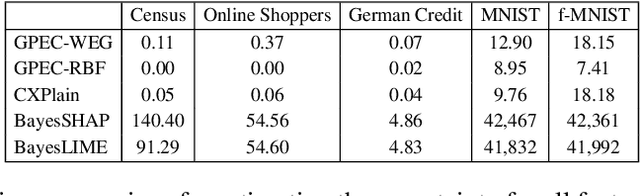
Post-hoc explanation methods have become increasingly depended upon for understanding black-box classifiers in high-stakes applications, precipitating a need for reliable explanations. While numerous explanation methods have been proposed, recent works have shown that many existing methods can be inconsistent or unstable. In addition, high-performing classifiers are often highly nonlinear and can exhibit complex behavior around the decision boundary, leading to brittle or misleading local explanations. Therefore, there is an impending need to quantify the uncertainty of such explanation methods in order to understand when explanations are trustworthy. We introduce a novel uncertainty quantification method parameterized by a Gaussian Process model, which combines the uncertainty approximation of existing methods with a novel geodesic-based similarity which captures the complexity of the target black-box decision boundary. The proposed framework is highly flexible; it can be used with any black-box classifier and feature attribution method to amortize uncertainty estimates for explanations. We show theoretically that our proposed geodesic-based kernel similarity increases with the complexity of the decision boundary. Empirical results on multiple tabular and image datasets show that our decision boundary-aware uncertainty estimate improves understanding of explanations as compared to existing methods.

Analyzing the Effects of Classifier Lipschitzness on Explainers

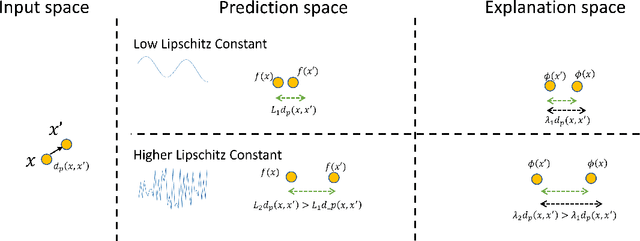
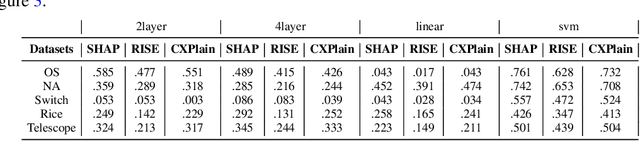
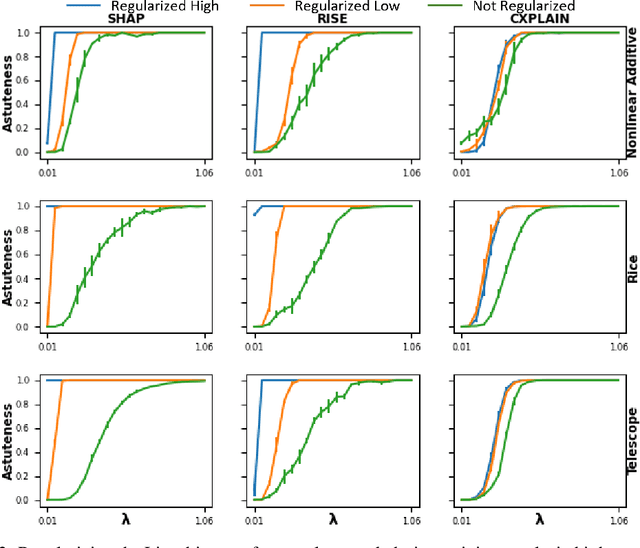
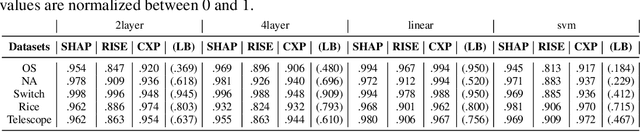
Machine learning methods are getting increasingly better at making predictions, but at the same time they are also becoming more complicated and less transparent. As a result, explainers are often relied on to provide interpretability to these black-box prediction models. As crucial diagnostics tools, it is important that these explainers themselves are reliable. In this paper we focus on one particular aspect of reliability, namely that an explainer should give similar explanations for similar data inputs. We formalize this notion by introducing and defining explainer astuteness, analogous to astuteness of classifiers. Our formalism is inspired by the concept of probabilistic Lipschitzness, which captures the probability of local smoothness of a function. For a variety of explainers (e.g., SHAP, RISE, CXPlain), we provide lower bound guarantees on the astuteness of these explainers given the Lipschitzness of the prediction function. These theoretical results imply that locally smooth prediction functions lend themselves to locally robust explanations. We evaluate these results empirically on simulated as well as real datasets.

Deep Layer-wise Networks Have Closed-Form Weights

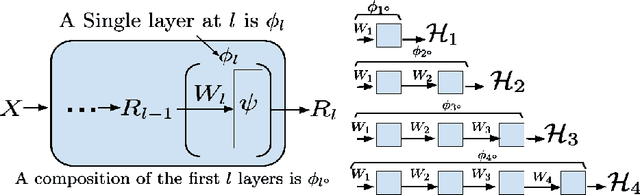
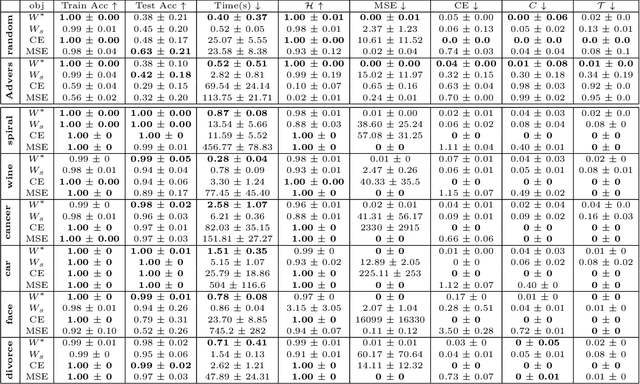
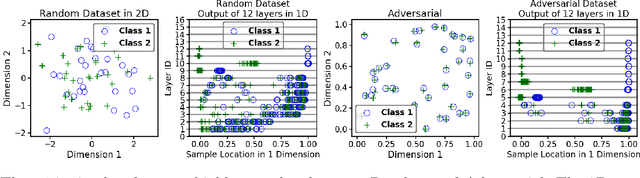
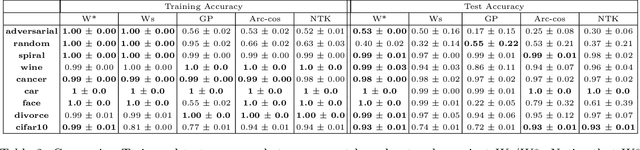
There is currently a debate within the neuroscience community over the likelihood of the brain performing backpropagation (BP). To better mimic the brain, training a network \textit{one layer at a time} with only a "single forward pass" has been proposed as an alternative to bypass BP; we refer to these networks as "layer-wise" networks. We continue the work on layer-wise networks by answering two outstanding questions. First, $\textit{do they have a closed-form solution?}$ Second, $\textit{how do we know when to stop adding more layers?}$ This work proves that the Kernel Mean Embedding is the closed-form weight that achieves the network global optimum while driving these networks to converge towards a highly desirable kernel for classification; we call it the $\textit{Neural Indicator Kernel}$.

Reliable Estimation of KL Divergence using a Discriminator in Reproducing Kernel Hilbert Space

Estimating Kullback Leibler (KL) divergence from samples of two distributions is essential in many machine learning problems. Variational methods using neural network discriminator have been proposed to achieve this task in a scalable manner. However, we noted that most of these methods using neural network discriminators suffer from high fluctuations (variance) in estimates and instability in training. In this paper, we look at this issue from statistical learning theory and function space complexity perspective to understand why this happens and how to solve it. We argue that the cause of these pathologies is lack of control over the complexity of the neural network discriminator function and could be mitigated by controlling it. To achieve this objective, we 1) present a novel construction of the discriminator in the Reproducing Kernel Hilbert Space (RKHS), 2) theoretically relate the error probability bound of the KL estimates to the complexity of the discriminator in the RKHS space, 3) present a scalable way to control the complexity (RKHS norm) of the discriminator for a reliable estimation of KL divergence, and 4) prove the consistency of the proposed estimator. In three different applications of KL divergence : estimation of KL, estimation of mutual information and Variational Bayes, we show that by controlling the complexity as developed in the theory, we are able to reduce the variance of KL estimates and stabilize the training