A surrogate model for topology optimisation of elastic structures via parametric autoencoders

A surrogate-based topology optimisation algorithm for linear elastic structures under parametric loads and boundary conditions is proposed. Instead of learning the parametric solution of the state (and adjoint) problems or the optimisation trajectory as a function of the iterations, the proposed approach devises a surrogate version of the entire optimisation pipeline. First, the method predicts a quasi-optimal topology for a given problem configuration as a surrogate model of high-fidelity topologies optimised with the homogenisation method. This is achieved by means of a feed-forward net learning the mapping between the input parameters characterising the system setup and a latent space determined by encoder/decoder blocks reducing the dimensionality of the parametric topology optimisation problem and reconstructing a high-dimensional representation of the topology. Then, the predicted topology is used as an educated initial guess for a computationally efficient algorithm penalising the intermediate values of the design variable, while enforcing the governing equations of the system. This step allows the method to correct potential errors introduced by the surrogate model, eliminate artifacts, and refine the design in order to produce topologies consistent with the underlying physics. Different architectures are proposed and the approximation and generalisation capabilities of the resulting models are numerically evaluated. The quasi-optimal topologies allow to outperform the high-fidelity optimiser by reducing the average number of optimisation iterations by $53\%$ while achieving discrepancies below $4\%$ in the optimal value of the objective functional, even in the challenging scenario of testing the model to extrapolate beyond the training and validation domain.

A kernel Principal Component Analysis (kPCA) digest with a new backward mapping (pre-image reconstruction) strategy

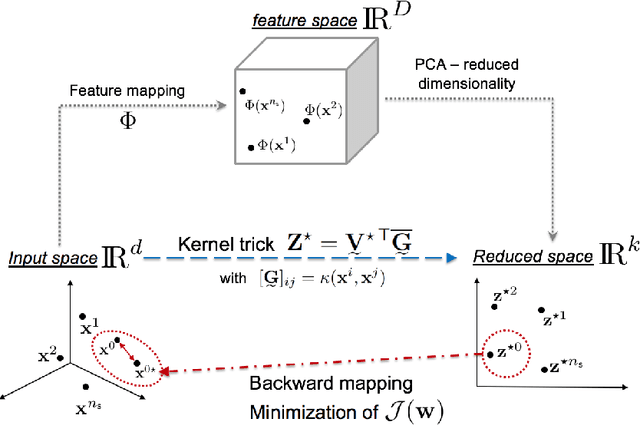
Methodologies for multidimensionality reduction aim at discovering low-dimensional manifolds where data ranges. Principal Component Analysis (PCA) is very effective if data have linear structure. But fails in identifying a possible dimensionality reduction if data belong to a nonlinear low-dimensional manifold. For nonlinear dimensionality reduction, kernel Principal Component Analysis (kPCA) is appreciated because of its simplicity and ease implementation. The paper provides a concise review of PCA and kPCA main ideas, trying to collect in a single document aspects that are often dispersed. Moreover, a strategy to map back the reduced dimension into the original high dimensional space is also devised, based on the minimization of a discrepancy functional.