A surrogate model for topology optimisation of elastic structures via parametric autoencoders

A surrogate-based topology optimisation algorithm for linear elastic structures under parametric loads and boundary conditions is proposed. Instead of learning the parametric solution of the state (and adjoint) problems or the optimisation trajectory as a function of the iterations, the proposed approach devises a surrogate version of the entire optimisation pipeline. First, the method predicts a quasi-optimal topology for a given problem configuration as a surrogate model of high-fidelity topologies optimised with the homogenisation method. This is achieved by means of a feed-forward net learning the mapping between the input parameters characterising the system setup and a latent space determined by encoder/decoder blocks reducing the dimensionality of the parametric topology optimisation problem and reconstructing a high-dimensional representation of the topology. Then, the predicted topology is used as an educated initial guess for a computationally efficient algorithm penalising the intermediate values of the design variable, while enforcing the governing equations of the system. This step allows the method to correct potential errors introduced by the surrogate model, eliminate artifacts, and refine the design in order to produce topologies consistent with the underlying physics. Different architectures are proposed and the approximation and generalisation capabilities of the resulting models are numerically evaluated. The quasi-optimal topologies allow to outperform the high-fidelity optimiser by reducing the average number of optimisation iterations by $53\%$ while achieving discrepancies below $4\%$ in the optimal value of the objective functional, even in the challenging scenario of testing the model to extrapolate beyond the training and validation domain.

Anisotropic mesh adaptation for region-based segmentation accounting for image spatial information

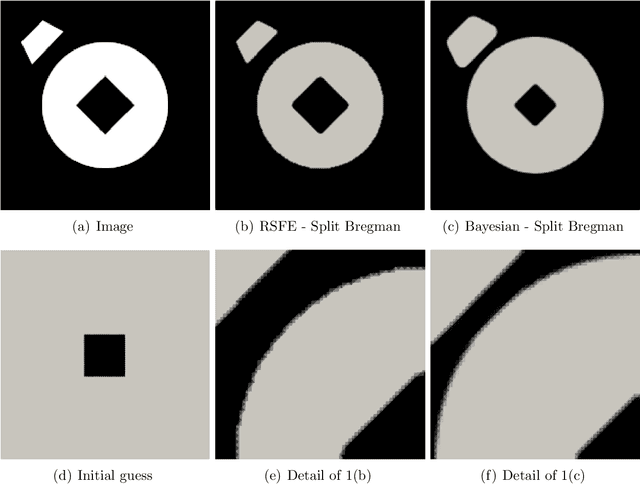
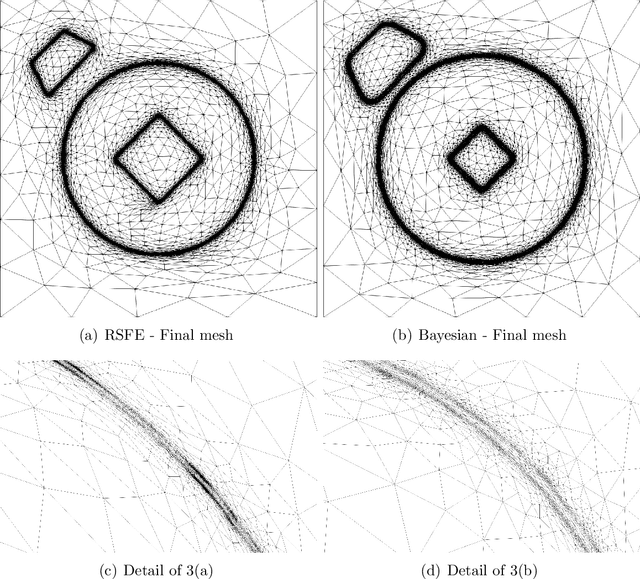
A finite element-based image segmentation strategy enhanced by an anisotropic mesh adaptation procedure is presented. The methodology relies on a split Bregman algorithm for the minimisation of a region-based energy functional and on an anisotropic recovery-based error estimate to drive mesh adaptation. More precisely, a Bayesian energy functional is considered to account for image spatial information, ensuring that the methodology is able to identify inhomogeneous spatial patterns in complex images. In addition, the anisotropic mesh adaptation guarantees a sharp detection of the interface between background and foreground of the image, with a reduced number of degrees of freedom. The resulting split-adapt Bregman algorithm is tested on a set of real images showing the accuracy and robustness of the method, even in the presence of Gaussian, salt and pepper and speckle noise.