Nonintrusive Uncertainty Quantification for automotive crash problems with VPS/Pamcrash

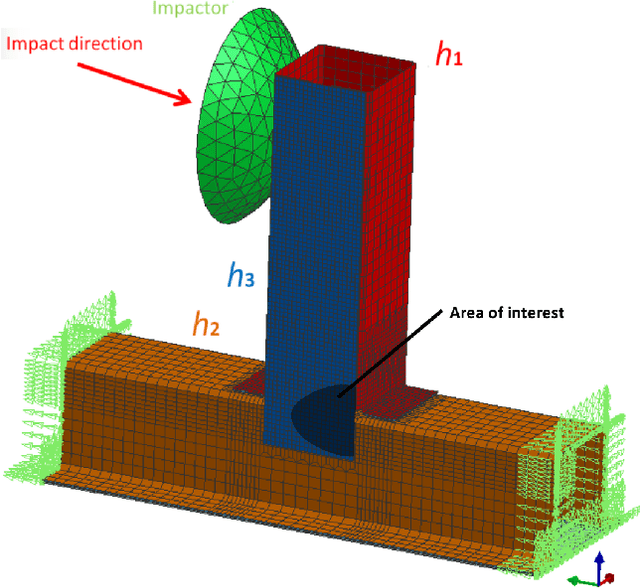
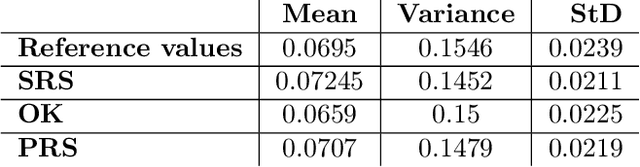
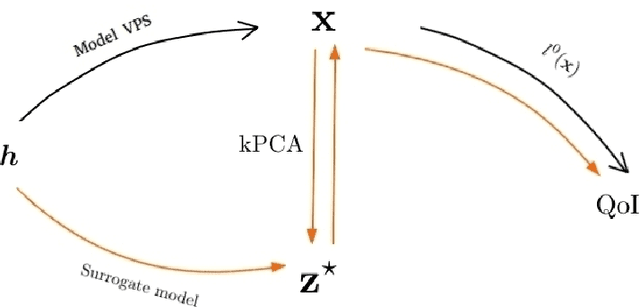
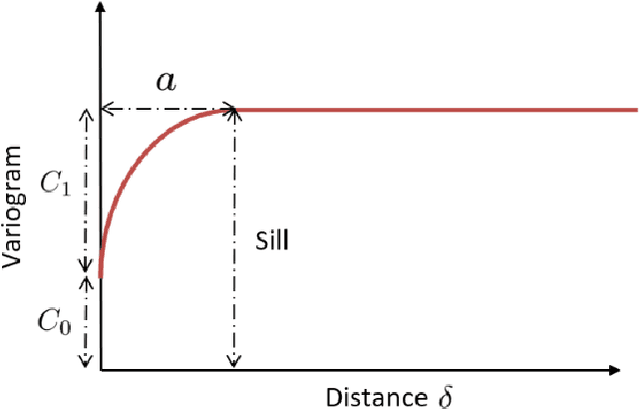
Uncertainty Quantification (UQ) is a key discipline for computational modeling of complex systems, enhancing reliability of engineering simulations. In crashworthiness, having an accurate assessment of the behavior of the model uncertainty allows reducing the number of prototypes and associated costs. Carrying out UQ in this framework is especially challenging because it requires highly expensive simulations. In this context, surrogate models (metamodels) allow drastically reducing the computational cost of Monte Carlo process. Different techniques to describe the metamodel are considered, Ordinary Kriging, Polynomial Response Surfaces and a novel strategy (based on Proper Generalized Decomposition) denoted by Separated Response Surface (SRS). A large number of uncertain input parameters may jeopardize the efficiency of the metamodels. Thus, previous to define a metamodel, kernel Principal Component Analysis (kPCA) is found to be effective to simplify the model outcome description. A benchmark crash test is used to show the efficiency of combining metamodels with kPCA.

A kernel Principal Component Analysis (kPCA) digest with a new backward mapping (pre-image reconstruction) strategy

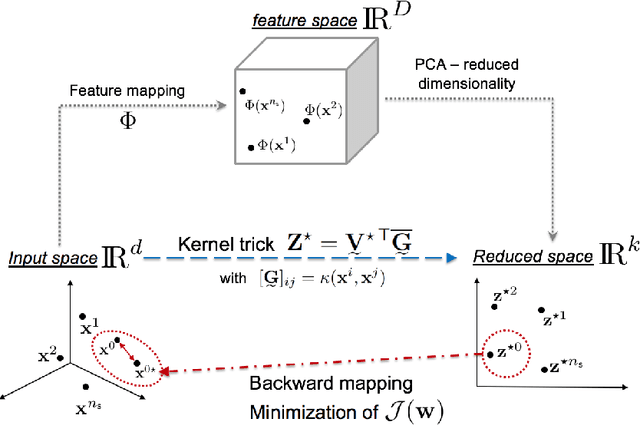
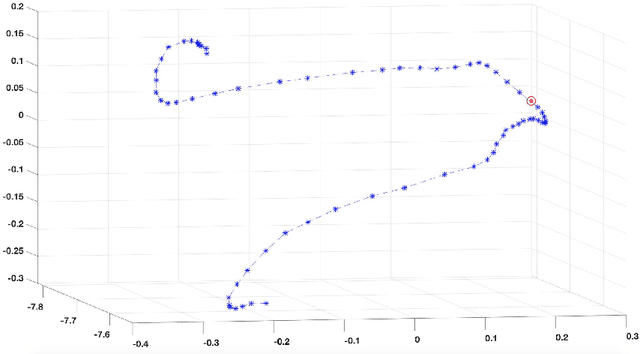
Methodologies for multidimensionality reduction aim at discovering low-dimensional manifolds where data ranges. Principal Component Analysis (PCA) is very effective if data have linear structure. But fails in identifying a possible dimensionality reduction if data belong to a nonlinear low-dimensional manifold. For nonlinear dimensionality reduction, kernel Principal Component Analysis (kPCA) is appreciated because of its simplicity and ease implementation. The paper provides a concise review of PCA and kPCA main ideas, trying to collect in a single document aspects that are often dispersed. Moreover, a strategy to map back the reduced dimension into the original high dimensional space is also devised, based on the minimization of a discrepancy functional.