A Nonlinear Separation Principle: Applications to Neural Networks, Control and Learning

This paper investigates continuous-time and discrete-time firing-rate and Hopfield recurrent neural networks (RNNs), with applications in nonlinear control design and implicit deep learning. First, we introduce a nonlinear separation principle that guarantees global exponential stability for the interconnection of a contracting state-feedback controller and a contracting observer, alongside parametric extensions for robustness and equilibrium tracking. Second, we derive sharp linear matrix inequality (LMI) conditions that guarantee the contractivity of both firing rate and Hopfield neural network architectures. We establish structural relationships among these certificates-demonstrating that continuous-time models with monotone non-decreasing activations maximize the admissible weight space, and extend these stability guarantees to interconnected systems and Graph RNNs. Third, we combine our separation principle and LMI framework to solve the output reference tracking problem for RNN-modeled plants. We provide LMI synthesis methods for feedback controllers and observers, and rigorously design a low-gain integral controller to eliminate steady-state error. Finally, we derive an exact, unconstrained algebraic parameterization of our contraction LMIs to design highly expressive implicit neural networks, achieving competitive accuracy and parameter efficiency on standard image classification benchmarks.

Opinion Dynamics Models for Sentiment Evolution in Weibo Blogs

Online social media platforms enable influencers to distribute content and quickly capture audience reactions, significantly shaping their promotional strategies and advertising agreements. Understanding how sentiment dynamics and emotional contagion unfold among followers is vital for influencers and marketers, as these processes shape engagement, brand perception, and purchasing behavior. While sentiment analysis tools effectively track sentiment fluctuations, dynamical models explaining their evolution remain limited, often neglecting network structures and interactions both among blogs and between their topic-focused follower groups. In this study, we tracked influential tech-focused Weibo bloggers over six months, quantifying follower sentiment from text-mined feedback. By treating each blogger's audience as a single "macro-agent", we find that sentiment trajectories follow the principle of iterative averaging -- a foundational mechanism in many dynamical models of opinion formation, a theoretical framework at the intersection of social network analysis and dynamical systems theory. The sentiment evolution aligns closely with opinion-dynamics models, particularly modified versions of the classical French-DeGroot model that incorporate delayed perception and distinguish between expressed and private opinions. The inferred influence structures reveal interdependencies among blogs that may arise from homophily, whereby emotionally similar users subscribe to the same blogs and collectively shape the shared sentiment expressed within these communities.

Robust Implicit Networks via Non-Euclidean Contractions

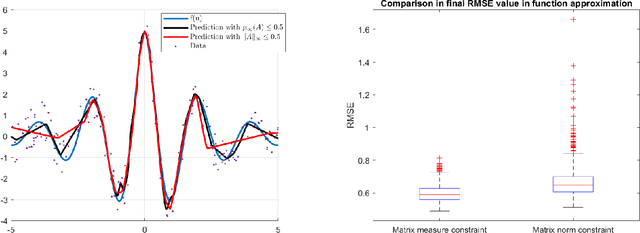
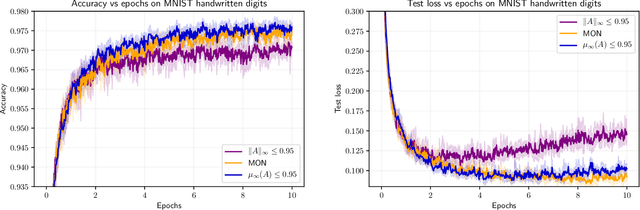
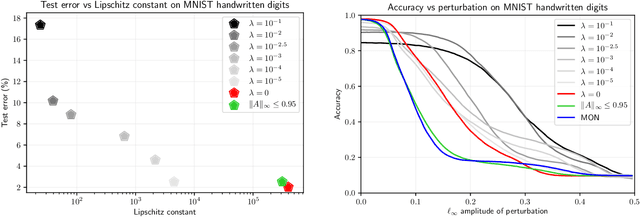
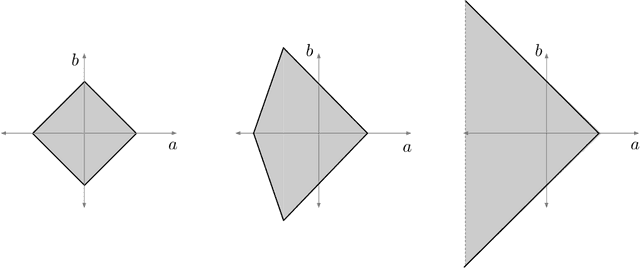
Implicit neural networks, a.k.a., deep equilibrium networks, are a class of implicit-depth learning models where function evaluation is performed by solving a fixed point equation. They generalize classic feedforward models and are equivalent to infinite-depth weight-tied feedforward networks. While implicit models show improved accuracy and significant reduction in memory consumption, they can suffer from ill-posedness and convergence instability. This paper provides a new framework to design well-posed and robust implicit neural networks based upon contraction theory for the non-Euclidean norm $\ell_\infty$. Our framework includes (i) a novel condition for well-posedness based on one-sided Lipschitz constants, (ii) an average iteration for computing fixed-points, and (iii) explicit estimates on input-output Lipschitz constants. Additionally, we design a training problem with the well-posedness condition and the average iteration as constraints and, to achieve robust models, with the input-output Lipschitz constant as a regularizer. Our $\ell_\infty$ well-posedness condition leads to a larger polytopic training search space than existing conditions and our average iteration enjoys accelerated convergence. Finally, we perform several numerical experiments for function estimation and digit classification through the MNIST data set. Our numerical results demonstrate improved accuracy and robustness of the implicit models with smaller input-output Lipschitz bounds.

A guiding vector field algorithm for path following control of nonholonomic mobile robots

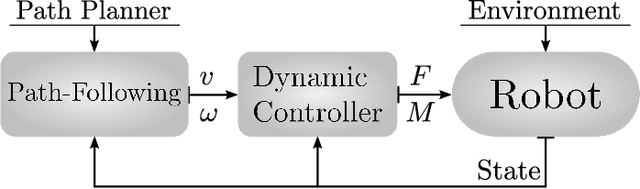
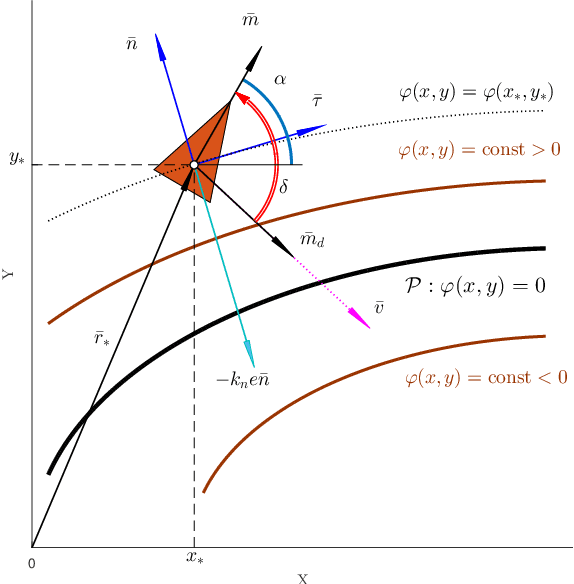
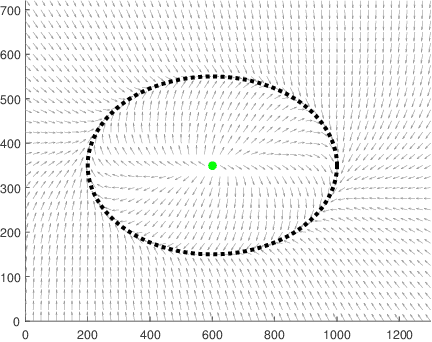
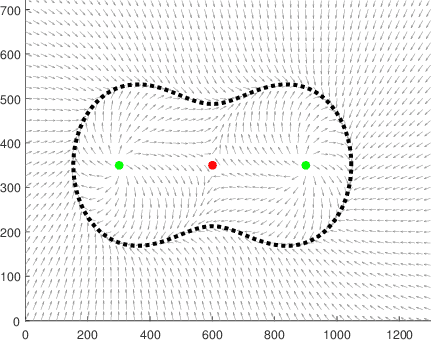
In this paper we propose an algorithm for path following control of the nonholonomic mobile robot based on the idea of the guiding vector field (GVF). The desired path may be an arbitrary smooth curve in its implicit form, that is, a level set of a predefined smooth function. Using this function and the robot's kinematic model, we design a GVF, whose integral curves converge to the trajectory. A nonlinear motion controller is then proposed which steers the robot along such an integral curve, bringing it to the desired path. We establish global convergence conditions for our algorithm and demonstrate its applicability and performance by experiments with real wheeled robots.