A Dynamic Regret Analysis and Adaptive Regularization Algorithm for On-Policy Robot Imitation Learning

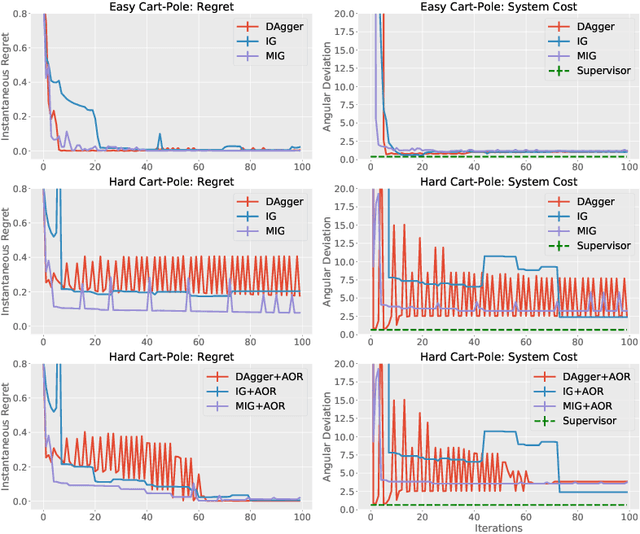
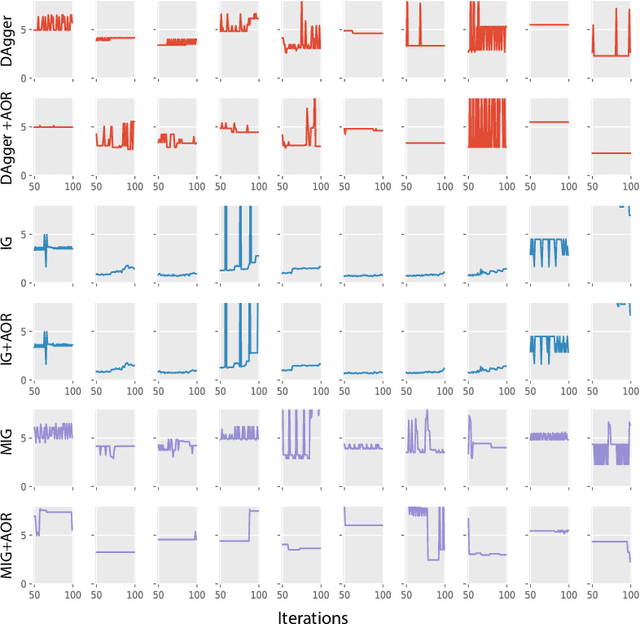
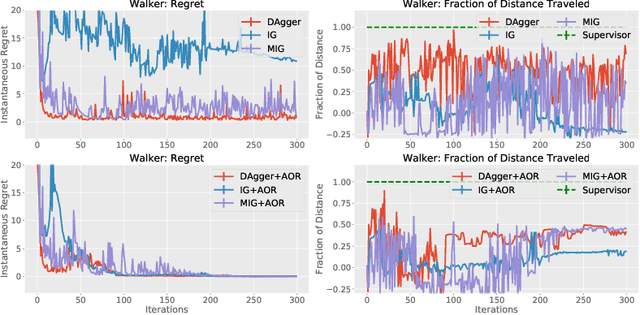
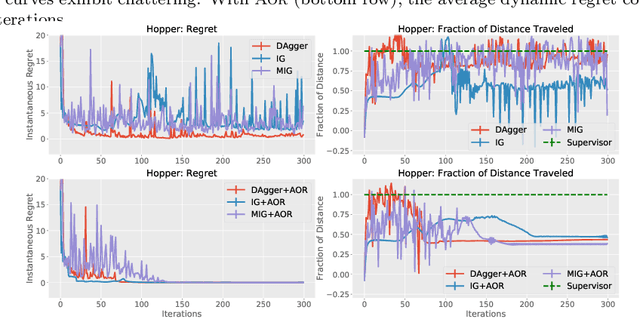
On-policy imitation learning algorithms such as Dagger evolve a robot control policy by executing it, measuring performance (loss), obtaining corrective feedback from a supervisor, and generating the next policy. As the loss between iterations can vary unpredictably, a fundamental question is under what conditions this process will eventually achieve a converged policy. If one assumes the underlying trajectory distribution is static (stationary), it is possible to prove convergence for Dagger. Cheng and Boots (2018) consider the more realistic model for robotics where the underlying trajectory distribution, which is a function of the policy, is dynamic and show that it is possible to prove convergence when a condition on the rate of change of the trajectory distributions is satisfied. In this paper, we reframe that result using dynamic regret theory from the field of Online Optimization to prove convergence to locally optimal policies for Dagger, Imitation Gradient, and Multiple Imitation Gradient. These results inspire a new algorithm, Adaptive On-Policy Regularization (AOR), that ensures the conditions for convergence. We present simulation results with cart-pole balancing and walker locomotion benchmarks that suggest AOR can significantly decrease dynamic regret and chattering. To our knowledge, this the first application of dynamic regret theory to imitation learning.

Convex Formulations for Fair Principal Component Analysis

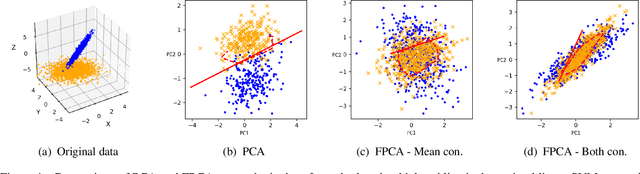
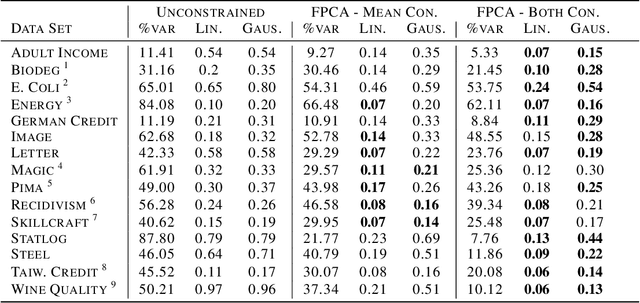
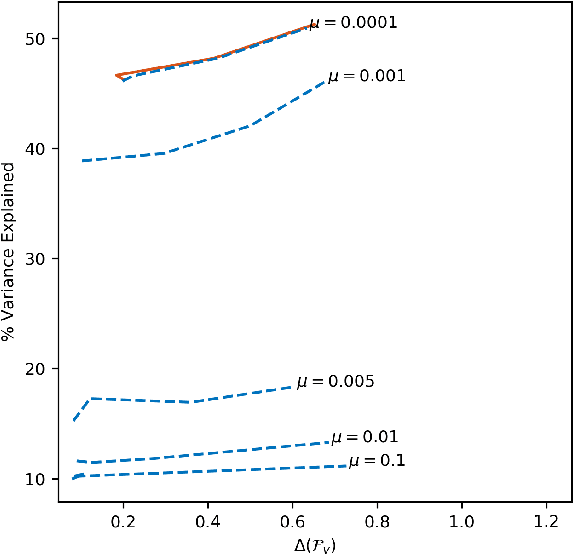
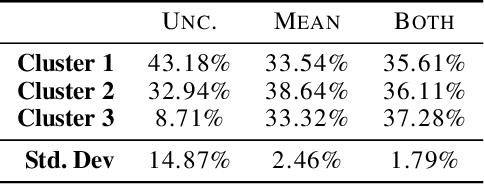
Though there is a growing body of literature on fairness for supervised learning, the problem of incorporating fairness into unsupervised learning has been less well-studied. This paper studies fairness in the context of principal component analysis (PCA). We first present a definition of fairness for dimensionality reduction, and our definition can be interpreted as saying that a reduction is fair if information about a protected class (e.g., race or gender) cannot be inferred from the dimensionality-reduced data points. Next, we develop convex optimization formulations that can improve the fairness (with respect to our definition) of PCA and kernel PCA. These formulations are semidefinite programs (SDP's), and we demonstrate the effectiveness of our formulations using several datasets. We conclude by showing how our approach can be used to perform a fair (with respect to age) clustering of health data that may be used to set health insurance rates.

Average Margin Regularization for Classifiers

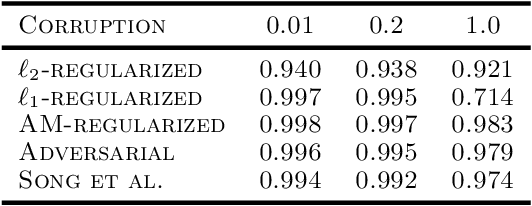
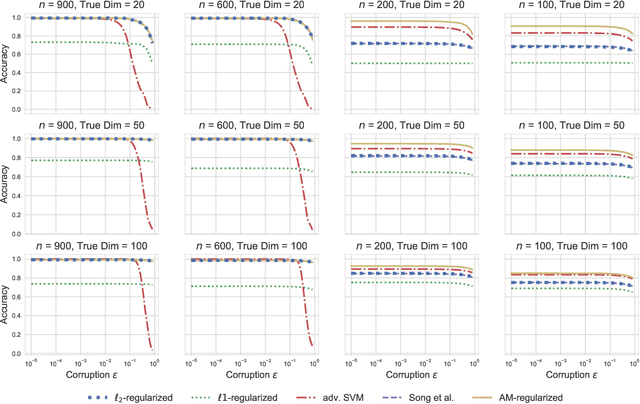
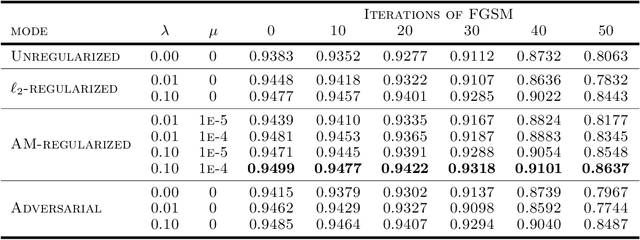
Adversarial robustness has become an important research topic given empirical demonstrations on the lack of robustness of deep neural networks. Unfortunately, recent theoretical results suggest that adversarial training induces a strict tradeoff between classification accuracy and adversarial robustness. In this paper, we propose and then study a new regularization for any margin classifier or deep neural network. We motivate this regularization by a novel generalization bound that shows a tradeoff in classifier accuracy between maximizing its margin and average margin. We thus call our approach an average margin (AM) regularization, and it consists of a linear term added to the objective. We theoretically show that for certain distributions AM regularization can both improve classifier accuracy and robustness to adversarial attacks. We conclude by using both synthetic and real data to empirically show that AM regularization can strictly improve both accuracy and robustness for support vector machine's (SVM's) and deep neural networks, relative to unregularized classifiers and adversarially trained classifiers.

Non-Stationary Bandits with Habituation and Recovery Dynamics

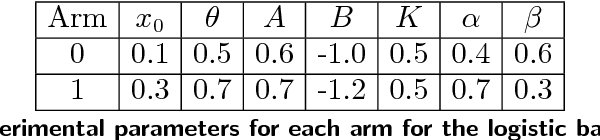
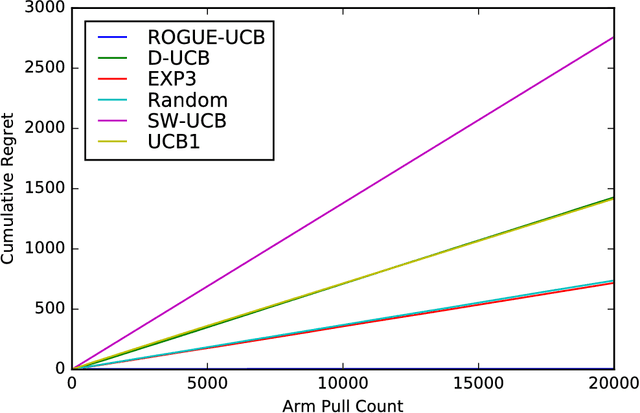
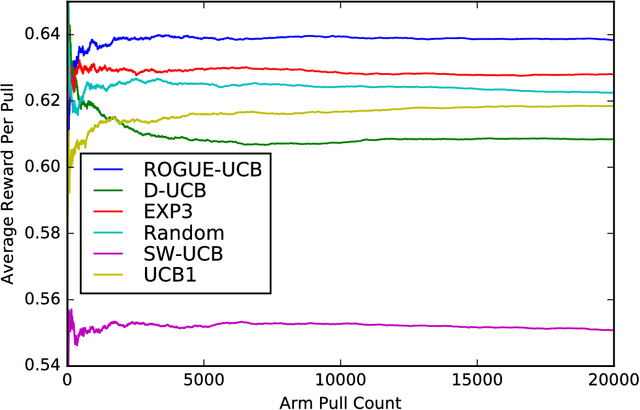
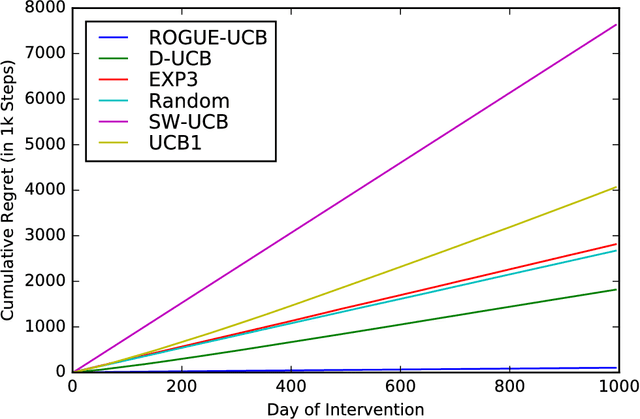
Many settings involve sequential decision-making where a set of actions can be chosen at each time step, each action provides a stochastic reward, and the distribution for the reward of each action is initially unknown. However, frequent selection of a specific action may reduce its expected reward, while abstaining from choosing an action may cause its expected reward to increase. Such non-stationary phenomena are observed in many real world settings such as personalized healthcare-adherence improving interventions and targeted online advertising. Though finding an optimal policy for general models with non-stationarity is PSPACE-complete, we propose and analyze a new class of models called ROGUE (Reducing or Gaining Unknown Efficacy) bandits, which we show in this paper can capture these phenomena and are amenable to the design of effective policies. We first present a consistent maximum likelihood estimator for the parameters of these models. Next, we construct finite sample concentration bounds that lead to an upper confidence bound policy called the ROGUE Upper Confidence Bound (ROGUE-UCB) algorithm. We prove that under proper conditions the ROGUE-UCB algorithm achieves logarithmic in time regret, unlike existing algorithms which result in linear regret. We conclude with a numerical experiment using real data from a personalized healthcare-adherence improving intervention to increase physical activity. In this intervention, the goal is to optimize the selection of messages (e.g., confidence increasing vs. knowledge increasing) to send to each individual each day to increase adherence and physical activity. Our results show that ROGUE-UCB performs better in terms of regret and average reward as compared to state of the art algorithms, and the use of ROGUE-UCB increases daily step counts by roughly 1,000 steps a day (about a half-mile more of walking) as compared to other algorithms.

Spectral Algorithms for Computing Fair Support Vector Machines

Classifiers and rating scores are prone to implicitly codifying biases, which may be present in the training data, against protected classes (i.e., age, gender, or race). So it is important to understand how to design classifiers and scores that prevent discrimination in predictions. This paper develops computationally tractable algorithms for designing accurate but fair support vector machines (SVM's). Our approach imposes a constraint on the covariance matrices conditioned on each protected class, which leads to a nonconvex quadratic constraint in the SVM formulation. We develop iterative algorithms to compute fair linear and kernel SVM's, which solve a sequence of relaxations constructed using a spectral decomposition of the nonconvex constraint. Its effectiveness in achieving high prediction accuracy while ensuring fairness is shown through numerical experiments on several data sets.

Low-Rank Approximation and Completion of Positive Tensors

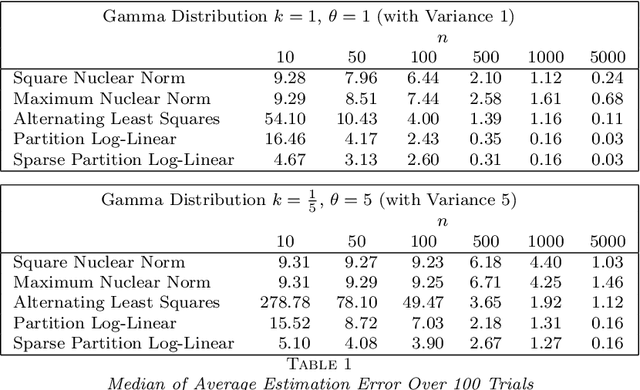
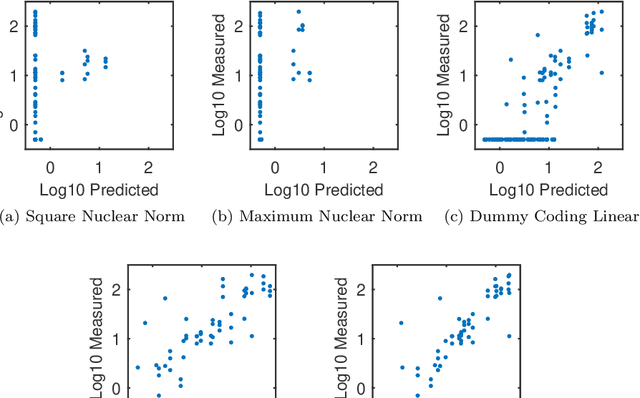
Unlike the matrix case, computing low-rank approximations of tensors is NP-hard and numerically ill-posed in general. Even the best rank-1 approximation of a tensor is NP-hard. In this paper, we use convex optimization to develop polynomial-time algorithms for low-rank approximation and completion of positive tensors. Our approach is to use algebraic topology to define a new (numerically well-posed) decomposition for positive tensors, which we show is equivalent to the standard tensor decomposition in important cases. Though computing this decomposition is a nonconvex optimization problem, we prove it can be exactly reformulated as a convex optimization problem. This allows us to construct polynomial-time randomized algorithms for computing this decomposition and for solving low-rank tensor approximation problems. Among the consequences is that best rank-1 approximations of positive tensors can be computed in polynomial time. Our framework is next extended to the tensor completion problem, where noisy entries of a tensor are observed and then used to estimate missing entries. We provide a polynomial-time algorithm that for specific cases requires a polynomial (in tensor order) number of measurements, in contrast to existing approaches that require an exponential number of measurements. These algorithms are extended to exploit sparsity in the tensor to reduce the number of measurements needed. We conclude by providing a novel interpretation of statistical regression problems with categorical variables as tensor completion problems, and numerical examples with synthetic data and data from a bioengineered metabolic network show the improved performance of our approach on this problem.

Practical Comparison of Optimization Algorithms for Learning-Based MPC with Linear Models

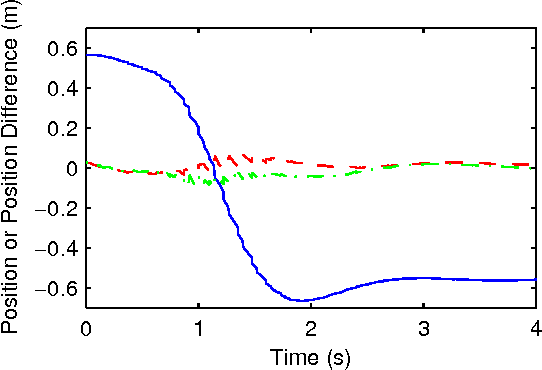
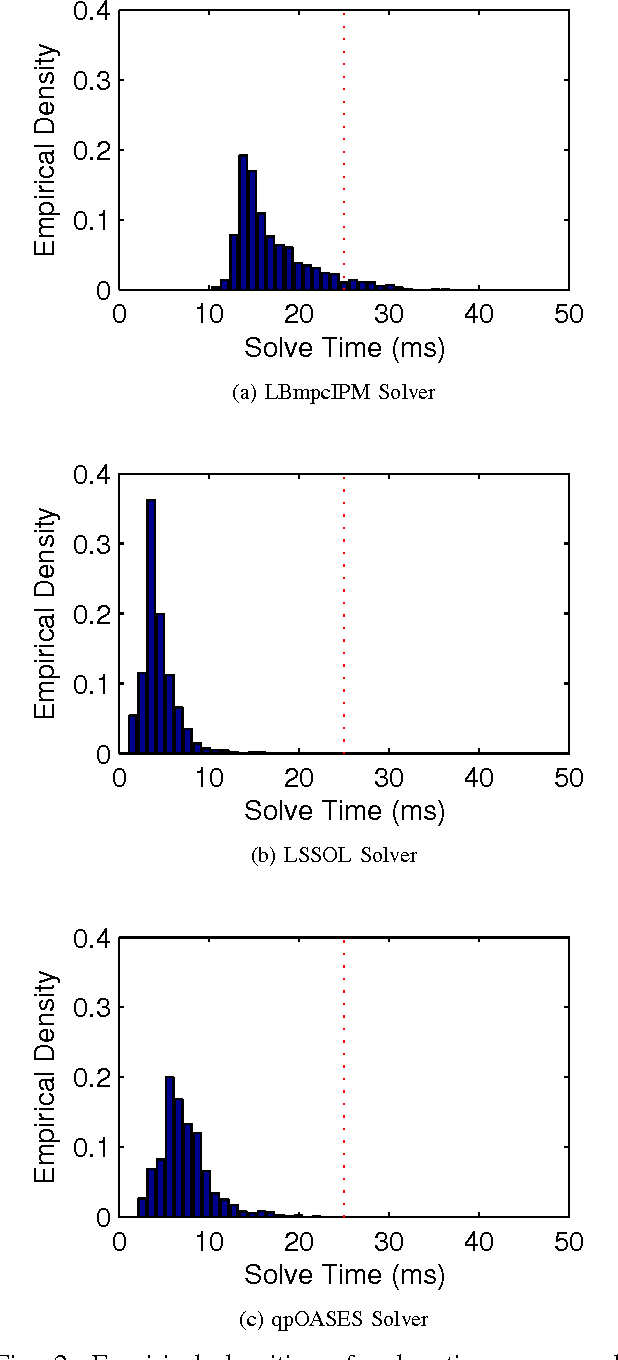
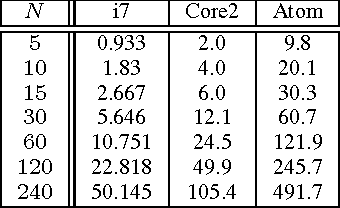
Learning-based control methods are an attractive approach for addressing performance and efficiency challenges in robotics and automation systems. One such technique that has found application in these domains is learning-based model predictive control (LBMPC). An important novelty of LBMPC lies in the fact that its robustness and stability properties are independent of the type of online learning used. This allows the use of advanced statistical or machine learning methods to provide the adaptation for the controller. This paper is concerned with providing practical comparisons of different optimization algorithms for implementing the LBMPC method, for the special case where the dynamic model of the system is linear and the online learning provides linear updates to the dynamic model. For comparison purposes, we have implemented a primal-dual infeasible start interior point method that exploits the sparsity structure of LBMPC. Our open source implementation (called LBmpcIPM) is available through a BSD license and is provided freely to enable the rapid implementation of LBMPC on other platforms. This solver is compared to the dense active set solvers LSSOL and qpOASES using a quadrotor helicopter platform. Two scenarios are considered: The first is a simulation comparing hovering control for the quadrotor, and the second is on-board control experiments of dynamic quadrotor flight. Though the LBmpcIPM method has better asymptotic computational complexity than LSSOL and qpOASES, we find that for certain integrated systems (like our quadrotor testbed) these methods can outperform LBmpcIPM. This suggests that actual benchmarks should be used when choosing which algorithm is used to implement LBMPC on practical systems.

Provably Safe and Robust Learning-Based Model Predictive Control

Controller design faces a trade-off between robustness and performance, and the reliability of linear controllers has caused many practitioners to focus on the former. However, there is renewed interest in improving system performance to deal with growing energy constraints. This paper describes a learning-based model predictive control (LBMPC) scheme that provides deterministic guarantees on robustness, while statistical identification tools are used to identify richer models of the system in order to improve performance; the benefits of this framework are that it handles state and input constraints, optimizes system performance with respect to a cost function, and can be designed to use a wide variety of parametric or nonparametric statistical tools. The main insight of LBMPC is that safety and performance can be decoupled under reasonable conditions in an optimization framework by maintaining two models of the system. The first is an approximate model with bounds on its uncertainty, and the second model is updated by statistical methods. LBMPC improves performance by choosing inputs that minimize a cost subject to the learned dynamics, and it ensures safety and robustness by checking whether these same inputs keep the approximate model stable when it is subject to uncertainty. Furthermore, we show that if the system is sufficiently excited, then the LBMPC control action probabilistically converges to that of an MPC computed using the true dynamics.

Statistical Results on Filtering and Epi-convergence for Learning-Based Model Predictive Control

Learning-based model predictive control (LBMPC) is a technique that provides deterministic guarantees on robustness, while statistical identification tools are used to identify richer models of the system in order to improve performance. This technical note provides proofs that elucidate the reasons for our choice of measurement model, as well as giving proofs concerning the stochastic convergence of LBMPC. The first part of this note discusses simultaneous state estimation and statistical identification (or learning) of unmodeled dynamics, for dynamical systems that can be described by ordinary differential equations (ODE's). The second part provides proofs concerning the epi-convergence of different statistical estimators that can be used with the learning-based model predictive control (LBMPC) technique. In particular, we prove results on the statistical properties of a nonparametric estimator that we have designed to have the correct deterministic and stochastic properties for numerical implementation when used in conjunction with LBMPC.

Energy-Efficient Building HVAC Control Using Hybrid System LBMPC

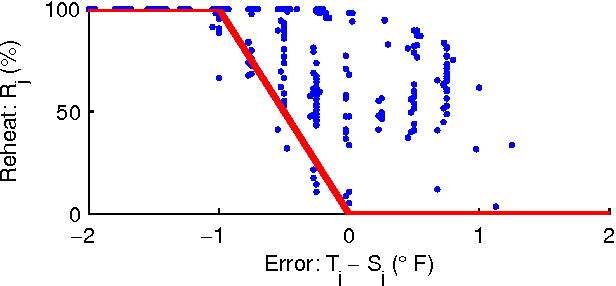
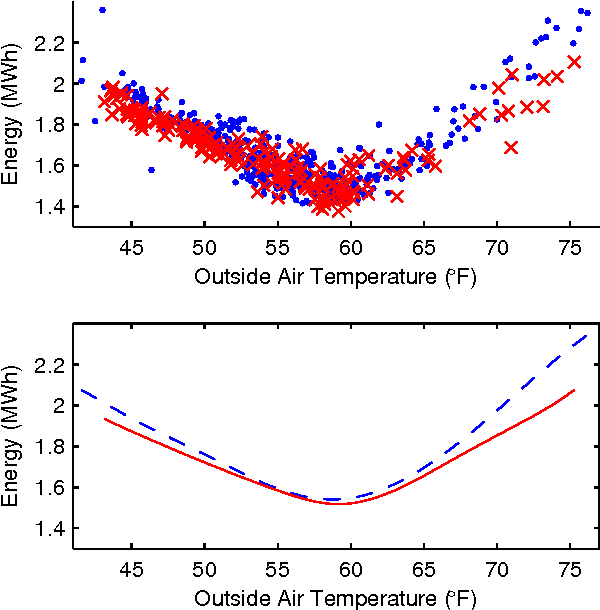
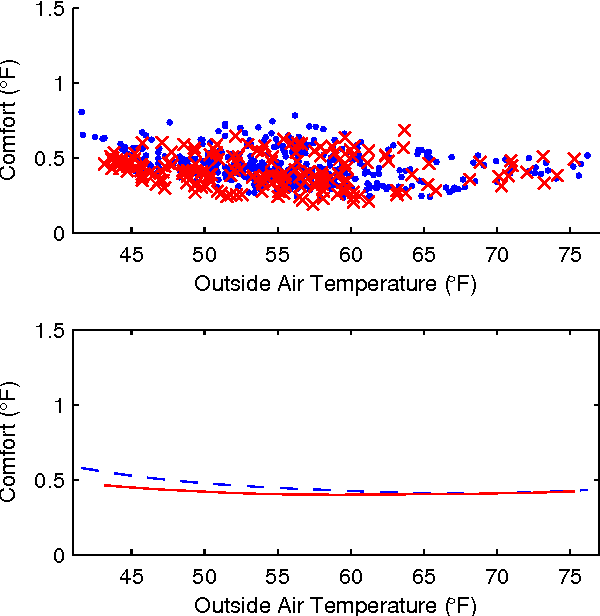
Improving the energy-efficiency of heating, ventilation, and air-conditioning (HVAC) systems has the potential to realize large economic and societal benefits. This paper concerns the system identification of a hybrid system model of a building-wide HVAC system and its subsequent control using a hybrid system formulation of learning-based model predictive control (LBMPC). Here, the learning refers to model updates to the hybrid system model that incorporate the heating effects due to occupancy, solar effects, outside air temperature (OAT), and equipment, in addition to integrator dynamics inherently present in low-level control. Though we make significant modeling simplifications, our corresponding controller that uses this model is able to experimentally achieve a large reduction in energy usage without any degradations in occupant comfort. It is in this way that we justify the modeling simplifications that we have made. We conclude by presenting results from experiments on our building HVAC testbed, which show an average of 1.5MWh of energy savings per day (p = 0.002) with a 95% confidence interval of 1.0MWh to 2.1MWh of energy savings.