Orthogonalized Estimation of Difference of $Q$-functions

Offline reinforcement learning is important in many settings with available observational data but the inability to deploy new policies online due to safety, cost, and other concerns. Many recent advances in causal inference and machine learning target estimation of causal contrast functions such as CATE, which is sufficient for optimizing decisions and can adapt to potentially smoother structure. We develop a dynamic generalization of the R-learner (Nie and Wager 2021, Lewis and Syrgkanis 2021) for estimating and optimizing the difference of $Q^\pi$-functions, $Q^\pi(s,1)-Q^\pi(s,0)$ (which can be used to optimize multiple-valued actions). We leverage orthogonal estimation to improve convergence rates in the presence of slower nuisance estimation rates and prove consistency of policy optimization under a margin condition. The method can leverage black-box nuisance estimators of the $Q$-function and behavior policy to target estimation of a more structured $Q$-function contrast.

Multi-CATE: Multi-Accurate Conditional Average Treatment Effect Estimation Robust to Unknown Covariate Shifts

Estimating heterogeneous treatment effects is important to tailor treatments to those individuals who would most likely benefit. However, conditional average treatment effect predictors may often be trained on one population but possibly deployed on different, possibly unknown populations. We use methodology for learning multi-accurate predictors to post-process CATE T-learners (differenced regressions) to become robust to unknown covariate shifts at the time of deployment. The method works in general for pseudo-outcome regression, such as the DR-learner. We show how this approach can combine (large) confounded observational and (smaller) randomized datasets by learning a confounded predictor from the observational dataset, and auditing for multi-accuracy on the randomized controlled trial. We show improvements in bias and mean squared error in simulations with increasingly larger covariate shift, and on a semi-synthetic case study of a parallel large observational study and smaller randomized controlled experiment. Overall, we establish a connection between methods developed for multi-distribution learning and achieve appealing desiderata (e.g. external validity) in causal inference and machine learning.

Reduced-Rank Multi-objective Policy Learning and Optimization

Evaluating the causal impacts of possible interventions is crucial for informing decision-making, especially towards improving access to opportunity. However, if causal effects are heterogeneous and predictable from covariates, personalized treatment decisions can improve individual outcomes and contribute to both efficiency and equity. In practice, however, causal researchers do not have a single outcome in mind a priori and often collect multiple outcomes of interest that are noisy estimates of the true target of interest. For example, in government-assisted social benefit programs, policymakers collect many outcomes to understand the multidimensional nature of poverty. The ultimate goal is to learn an optimal treatment policy that in some sense maximizes multiple outcomes simultaneously. To address such issues, we present a data-driven dimensionality-reduction methodology for multiple outcomes in the context of optimal policy learning with multiple objectives. We learn a low-dimensional representation of the true outcome from the observed outcomes using reduced rank regression. We develop a suite of estimates that use the model to denoise observed outcomes, including commonly-used index weightings. These methods improve estimation error in policy evaluation and optimization, including on a case study of real-world cash transfer and social intervention data. Reducing the variance of noisy social outcomes can improve the performance of algorithmic allocations.

Reward-Relevance-Filtered Linear Offline Reinforcement Learning

This paper studies offline reinforcement learning with linear function approximation in a setting with decision-theoretic, but not estimation sparsity. The structural restrictions of the data-generating process presume that the transitions factor into a sparse component that affects the reward and could affect additional exogenous dynamics that do not affect the reward. Although the minimally sufficient adjustment set for estimation of full-state transition properties depends on the whole state, the optimal policy and therefore state-action value function depends only on the sparse component: we call this causal/decision-theoretic sparsity. We develop a method for reward-filtering the estimation of the state-action value function to the sparse component by a modification of thresholded lasso in least-squares policy evaluation. We provide theoretical guarantees for our reward-filtered linear fitted-Q-iteration, with sample complexity depending only on the size of the sparse component.

Optimal and Fair Encouragement Policy Evaluation and Learning

In consequential domains, it is often impossible to compel individuals to take treatment, so that optimal policy rules are merely suggestions in the presence of human non-adherence to treatment recommendations. In these same domains, there may be heterogeneity both in who responds in taking-up treatment, and heterogeneity in treatment efficacy. While optimal treatment rules can maximize causal outcomes across the population, access parity constraints or other fairness considerations can be relevant in the case of encouragement. For example, in social services, a persistent puzzle is the gap in take-up of beneficial services among those who may benefit from them the most. When in addition the decision-maker has distributional preferences over both access and average outcomes, the optimal decision rule changes. We study causal identification, statistical variance-reduced estimation, and robust estimation of optimal treatment rules, including under potential violations of positivity. We consider fairness constraints such as demographic parity in treatment take-up, and other constraints, via constrained optimization. Our framework can be extended to handle algorithmic recommendations under an often-reasonable covariate-conditional exclusion restriction, using our robustness checks for lack of positivity in the recommendation. We develop a two-stage algorithm for solving over parametrized policy classes under general constraints to obtain variance-sensitive regret bounds. We illustrate the methods in two case studies based on data from randomized encouragement to enroll in insurance and from pretrial supervised release with electronic monitoring.

Robust Fitted-Q-Evaluation and Iteration under Sequentially Exogenous Unobserved Confounders

Offline reinforcement learning is important in domains such as medicine, economics, and e-commerce where online experimentation is costly, dangerous or unethical, and where the true model is unknown. However, most methods assume all covariates used in the behavior policy's action decisions are observed. This untestable assumption may be incorrect. We study robust policy evaluation and policy optimization in the presence of unobserved confounders. We assume the extent of possible unobserved confounding can be bounded by a sensitivity model, and that the unobserved confounders are sequentially exogenous. We propose and analyze an (orthogonalized) robust fitted-Q-iteration that uses closed-form solutions of the robust Bellman operator to derive a loss minimization problem for the robust Q function. Our algorithm enjoys the computational ease of fitted-Q-iteration and statistical improvements (reduced dependence on quantile estimation error) from orthogonalization. We provide sample complexity bounds, insights, and show effectiveness in simulations.

A Note on Task-Aware Loss via Reweighing Prediction Loss by Decision-Regret

In this short technical note we propose a baseline for decision-aware learning for contextual linear optimization, which solves stochastic linear optimization when cost coefficients can be predicted based on context information. We propose a decision-aware version of predict-then-optimize. We reweigh the prediction error by the decision regret incurred by an (unweighted) pilot estimator of costs to obtain a decision-aware predictor, then optimize with cost predictions from the decision-aware predictor. This method can be motivated as a finite-difference, iterate-independent approximation of the gradients of previously proposed end-to-end learning algorithms; it is also consistent with previously suggested intuition for end-to-end learning. This baseline is computationally easy to implement with readily available reweighted prediction oracles and linear optimization, and can be implemented with convex optimization so long as the prediction error minimization is convex. Empirically, we demonstrate that this approach can lead to improvements over a "predict-then-optimize" framework for settings with misspecified models, and is competitive with other end-to-end approaches. Therefore, due to its simplicity and ease of use, we suggest it as a simple baseline for end-to-end and decision-aware learning.

Empirical Gateaux Derivatives for Causal Inference

We study a constructive algorithm that approximates Gateaux derivatives for statistical functionals by finite-differencing, with a focus on causal inference functionals. We consider the case where probability distributions are not known a priori but also need to be estimated from data. These estimated distributions lead to empirical Gateaux derivatives, and we study the relationships between empirical, numerical, and analytical Gateaux derivatives. Starting with a case study of estimating the mean potential outcome (hence average treatment effect), we instantiate the exact relationship between finite-differences and the analytical Gateaux derivative. We then derive requirements on the rates of numerical approximation in perturbation and smoothing that preserve the statistical benefits of one-step adjustments, such as rate-double-robustness. We then study more complicated functionals such as dynamic treatment regimes and the linear-programming formulation for policy optimization in infinite-horizon Markov decision processes. The newfound ability to approximate bias adjustments in the presence of arbitrary constraints illustrates the usefulness of constructive approaches for Gateaux derivatives. We also find that the statistical structure of the functional (rate-double robustness) can permit less conservative rates of finite-difference approximation. This property, however, can be specific to particular functionals, e.g. it occurs for the mean potential outcome (hence average treatment effect) but not the infinite-horizon MDP policy value.

Off-Policy Evaluation with Policy-Dependent Optimization Response

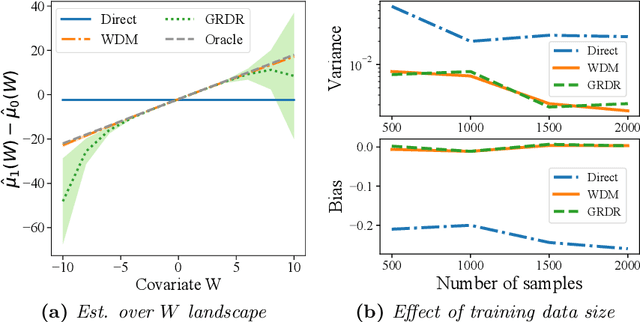
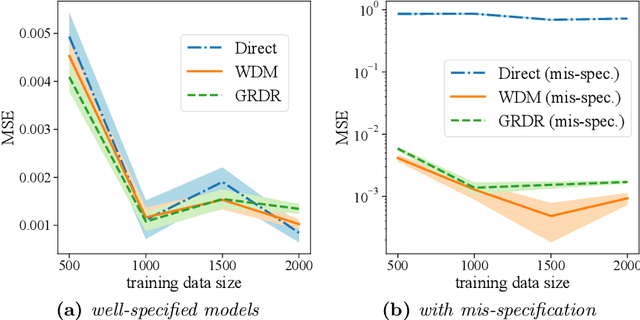
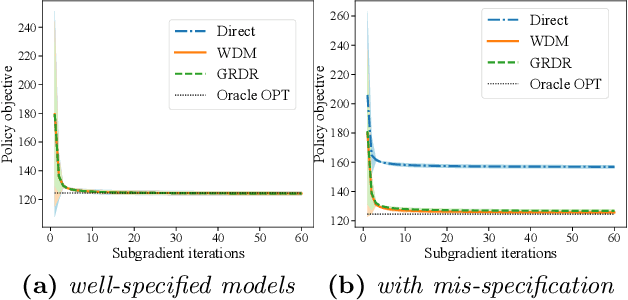
The intersection of causal inference and machine learning for decision-making is rapidly expanding, but the default decision criterion remains an \textit{average} of individual causal outcomes across a population. In practice, various operational restrictions ensure that a decision-maker's utility is not realized as an \textit{average} but rather as an \textit{output} of a downstream decision-making problem (such as matching, assignment, network flow, minimizing predictive risk). In this work, we develop a new framework for off-policy evaluation with a \textit{policy-dependent} linear optimization response: causal outcomes introduce stochasticity in objective function coefficients. In this framework, a decision-maker's utility depends on the policy-dependent optimization, which introduces a fundamental challenge of \textit{optimization} bias even for the case of policy evaluation. We construct unbiased estimators for the policy-dependent estimand by a perturbation method. We also discuss the asymptotic variance properties for a set of plug-in regression estimators adjusted to be compatible with that perturbation method. Lastly, attaining unbiased policy evaluation allows for policy optimization, and we provide a general algorithm for optimizing causal interventions. We corroborate our theoretical results with numerical simulations.

Stateful Offline Contextual Policy Evaluation and Learning

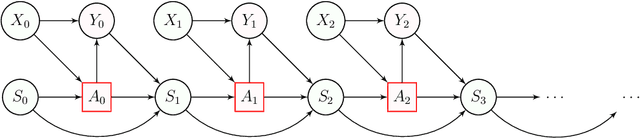
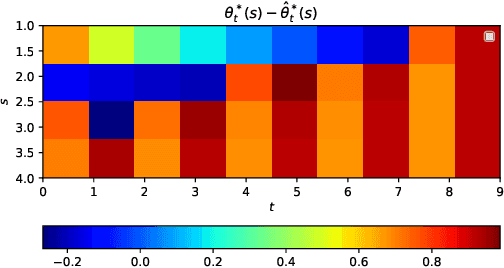
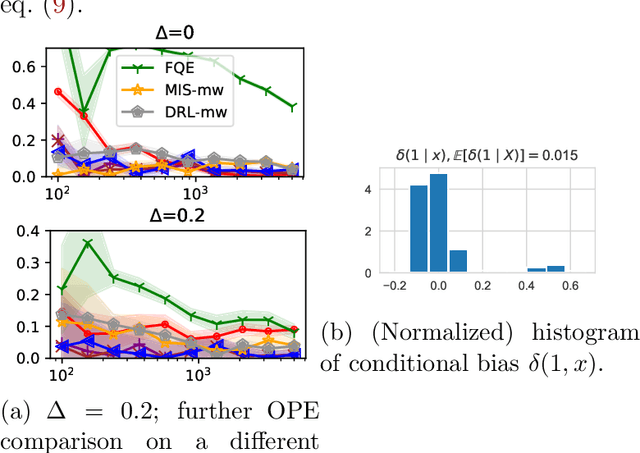
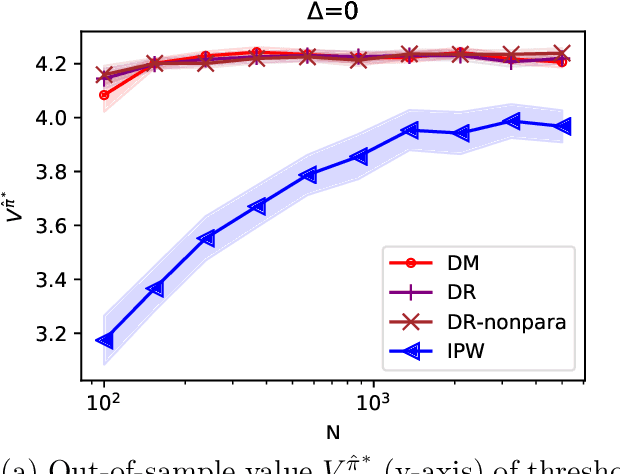
We study off-policy evaluation and learning from sequential data in a structured class of Markov decision processes that arise from repeated interactions with an exogenous sequence of arrivals with contexts, which generate unknown individual-level responses to agent actions. This model can be thought of as an offline generalization of contextual bandits with resource constraints. We formalize the relevant causal structure of problems such as dynamic personalized pricing and other operations management problems in the presence of potentially high-dimensional user types. The key insight is that an individual-level response is often not causally affected by the state variable and can therefore easily be generalized across timesteps and states. When this is true, we study implications for (doubly robust) off-policy evaluation and learning by instead leveraging single time-step evaluation, estimating the expectation over a single arrival via data from a population, for fitted-value iteration in a marginal MDP. We study sample complexity and analyze error amplification that leads to the persistence, rather than attenuation, of confounding error over time. In simulations of dynamic and capacitated pricing, we show improved out-of-sample policy performance in this class of relevant problems.