A Physics-Informed Vector Quantized Autoencoder for Data Compression of Turbulent Flow

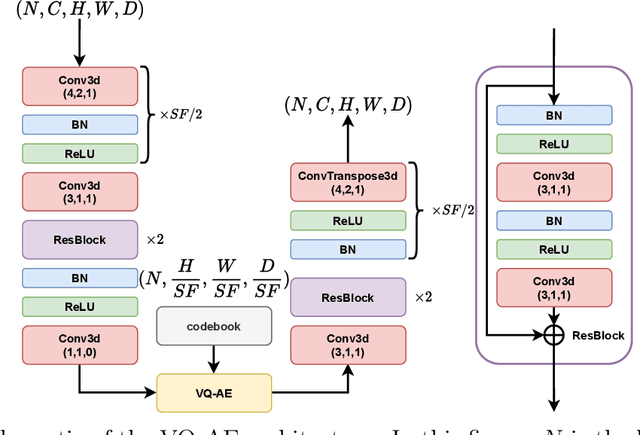
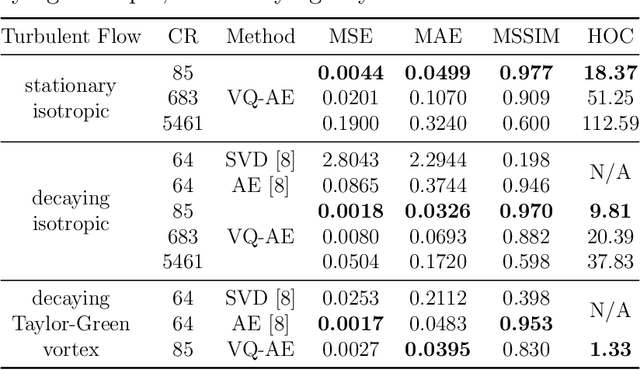
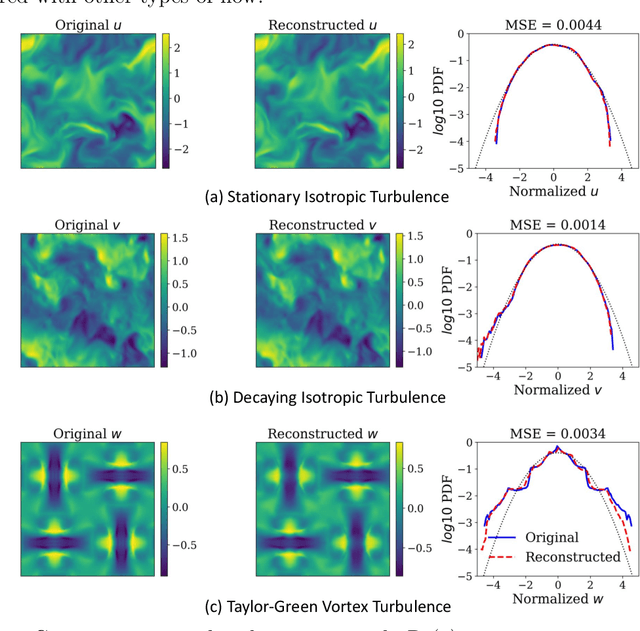
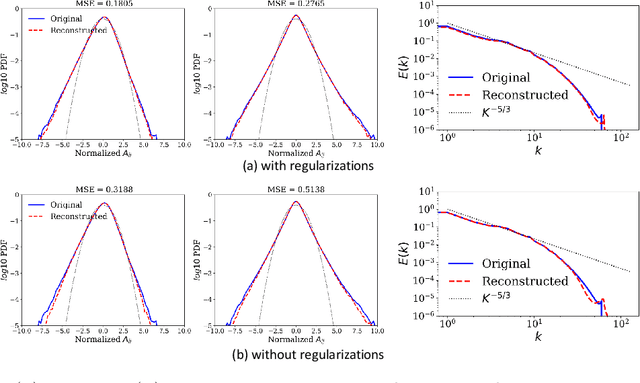
Analyzing large-scale data from simulations of turbulent flows is memory intensive, requiring significant resources. This major challenge highlights the need for data compression techniques. In this study, we apply a physics-informed Deep Learning technique based on vector quantization to generate a discrete, low-dimensional representation of data from simulations of three-dimensional turbulent flows. The deep learning framework is composed of convolutional layers and incorporates physical constraints on the flow, such as preserving incompressibility and global statistical characteristics of the velocity gradients. The accuracy of the model is assessed using statistical, comparison-based similarity and physics-based metrics. The training data set is produced from Direct Numerical Simulation of an incompressible, statistically stationary, isotropic turbulent flow. The performance of this lossy data compression scheme is evaluated not only with unseen data from the stationary, isotropic turbulent flow, but also with data from decaying isotropic turbulence, and a Taylor-Green vortex flow. Defining the compression ratio (CR) as the ratio of original data size to the compressed one, the results show that our model based on vector quantization can offer CR $=85$ with a mean square error (MSE) of $O(10^{-3})$, and predictions that faithfully reproduce the statistics of the flow, except at the very smallest scales where there is some loss. Compared to the recent study based on a conventional autoencoder where compression is performed in a continuous space, our model improves the CR by more than $30$ percent, and reduces the MSE by an order of magnitude. Our compression model is an attractive solution for situations where fast, high quality and low-overhead encoding and decoding of large data are required.

Emulating Spatio-Temporal Realizations of Three-Dimensional Isotropic Turbulence via Deep Sequence Learning Models

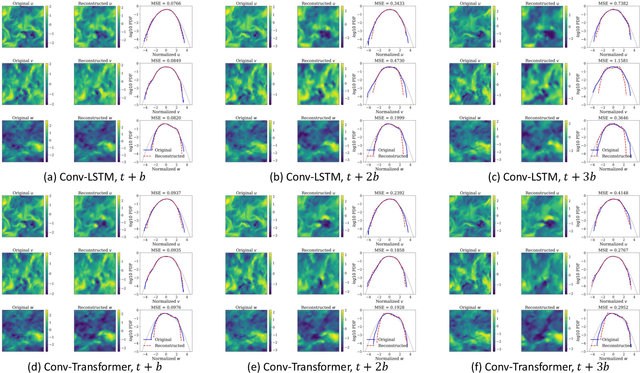
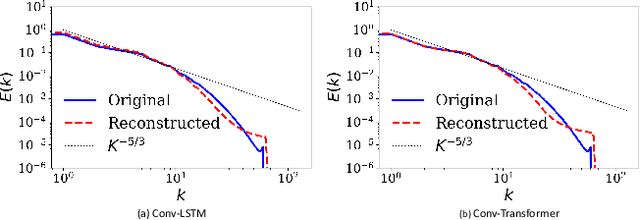
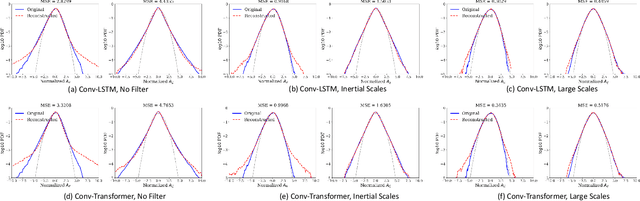
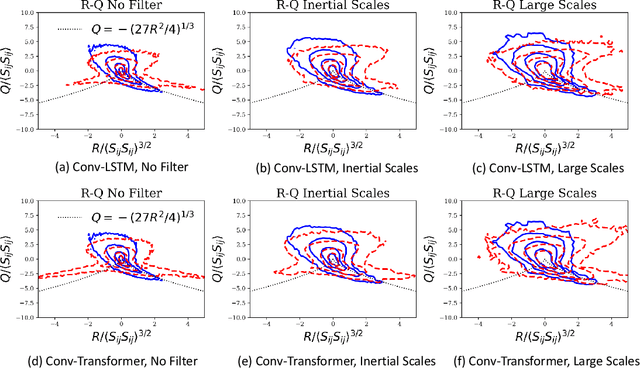
We use a data-driven approach to model a three-dimensional turbulent flow using cutting-edge Deep Learning techniques. The deep learning framework incorporates physical constraints on the flow, such as preserving incompressibility and global statistical invariants of velocity gradient tensor. The accuracy of the model is assessed using statistical and physics-based metrics. The data set comes from Direct Numerical Simulation of an incompressible, statistically stationary, isotropic turbulent flow in a cubic box. Since the size of the dataset is memory intensive, we first generate a low-dimensional representation of the velocity data, and then pass it to a sequence prediction network that learns the spatial and temporal correlations of the underlying data. The dimensionality reduction is performed via extraction using Vector-Quantized Autoencoder (VQ-AE), which learns the discrete latent variables. For the sequence forecasting, the idea of Transformer architecture from natural language processing is used, and its performance compared against more standard Recurrent Networks (such as Convolutional LSTM). These architectures are designed and trained to perform a sequence to sequence multi-class classification task in which they take an input sequence with a fixed length (k) and predict a sequence with a fixed length (p), representing the future time instants of the flow. Our results for the short-term predictions show that the accuracy of results for both models deteriorates across predicted snapshots due to autoregressive nature of the predictions. Based on our diagnostics tests, the trained Conv-Transformer model outperforms the Conv-LSTM one and can accurately, both quantitatively and qualitatively, retain the large scales and capture well the inertial scales of flow but fails at recovering the small and intermittent fluid motions.