Andrew A. Li
Best of Many in Both Worlds: Online Resource Allocation with Predictions under Unknown Arrival Model
Feb 21, 2024

Abstract:Online decision-makers today can often obtain predictions on future variables, such as arrivals, demands, inventories, and so on. These predictions can be generated from simple forecasting algorithms for univariate time-series, all the way to state-of-the-art machine learning models that leverage multiple time-series and additional feature information. However, the prediction quality is often unknown to decisions-makers a priori, hence blindly following the predictions can be harmful. In this paper, we address this problem by giving algorithms that take predictions as inputs and perform robustly against the unknown prediction quality. We consider the online resource allocation problem, one of the most generic models in revenue management and online decision-making. In this problem, a decision maker has a limited amount of resources, and requests arrive sequentially. For each request, the decision-maker needs to decide on an action, which generates a certain amount of rewards and consumes a certain amount of resources, without knowing the future requests. The decision-maker's objective is to maximize the total rewards subject to resource constraints. We take the shadow price of each resource as prediction, which can be obtained by predictions on future requests. Prediction quality is naturally defined to be the $\ell_1$ distance between the prediction and the actual shadow price. Our main contribution is an algorithm which takes the prediction of unknown quality as an input, and achieves asymptotically optimal performance under both requests arrival models (stochastic and adversarial) without knowing the prediction quality and the requests arrival model beforehand. We show our algorithm's performance matches the best achievable performance of any algorithm had the arrival models and the accuracy of the predictions been known. We empirically validate our algorithm with experiments.
Modeling Choice via Self-Attention
Nov 11, 2023



Abstract:Models of choice are a fundamental input to many now-canonical optimization problems in the field of Operations Management, including assortment, inventory, and price optimization. Naturally, accurate estimation of these models from data is a critical step in the application of these optimization problems in practice, and so it is perhaps surprising that such choice estimation has to now been accomplished almost exclusively, both in theory and in practice, (a) without the use of deep learning in any meaningful way, and (b) via evaluation on limited data with constantly-changing metrics. This is in stark contrast to the vast majority of similar learning applications, for which the practice of machine learning suggests that (a) neural network-based models are typically state-of-the-art, and (b) strict standardization on evaluation procedures (datasets, metrics, etc.) is crucial. Thus motivated, we first propose a choice model that is the first to successfully (both theoretically and practically) leverage a modern neural network architectural concept (self-attention). Theoretically, we show that our attention-based choice model is a low-rank generalization of the Halo Multinomial Logit model, a recent model that parsimoniously captures irrational choice effects and has seen empirical success. We prove that whereas the Halo-MNL requires $\Omega(m^2)$ data samples to estimate, where $m$ is the number of products, our model supports a natural nonconvex estimator (in particular, that which a standard neural network implementation would apply) which admits a near-optimal stationary point with $O(m)$ samples. We then establish the first realistic-scale benchmark for choice estimation on real data and use this benchmark to run the largest evaluation of existing choice models to date. We find that the model we propose is dominant over both short-term and long-term data periods.
Markovian Interference in Experiments
Jun 09, 2022

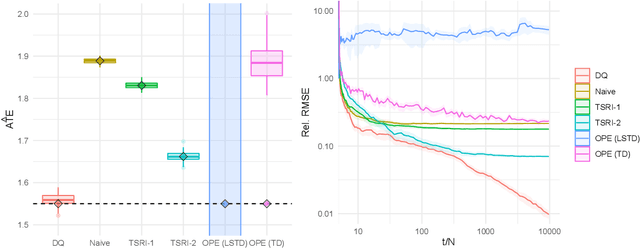
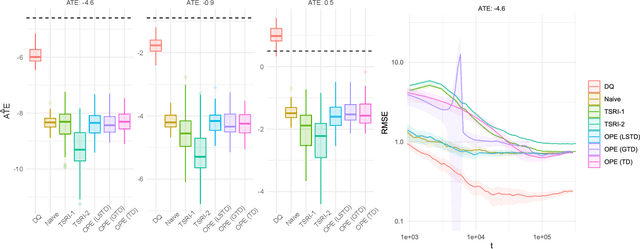
Abstract:We consider experiments in dynamical systems where interventions on some experimental units impact other units through a limiting constraint (such as a limited inventory). Despite outsize practical importance, the best estimators for this `Markovian' interference problem are largely heuristic in nature, and their bias is not well understood. We formalize the problem of inference in such experiments as one of policy evaluation. Off-policy estimators, while unbiased, apparently incur a large penalty in variance relative to state-of-the-art heuristics. We introduce an on-policy estimator: the Differences-In-Q's (DQ) estimator. We show that the DQ estimator can in general have exponentially smaller variance than off-policy evaluation. At the same time, its bias is second order in the impact of the intervention. This yields a striking bias-variance tradeoff so that the DQ estimator effectively dominates state-of-the-art alternatives. From a theoretical perspective, we introduce three separate novel techniques that are of independent interest in the theory of Reinforcement Learning (RL). Our empirical evaluation includes a set of experiments on a city-scale ride-hailing simulator.
Uncertainty Quantification For Low-Rank Matrix Completion With Heterogeneous and Sub-Exponential Noise
Oct 22, 2021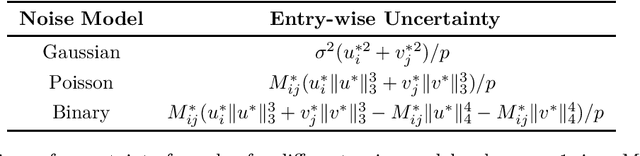
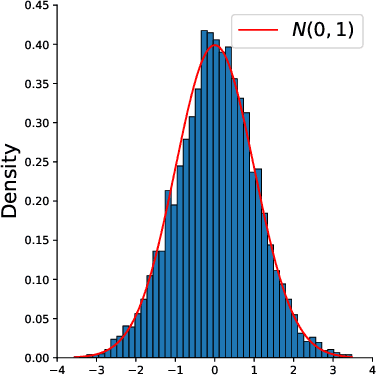
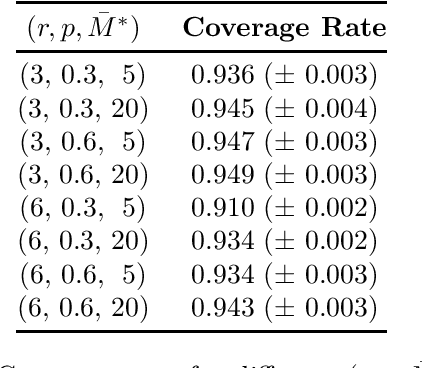
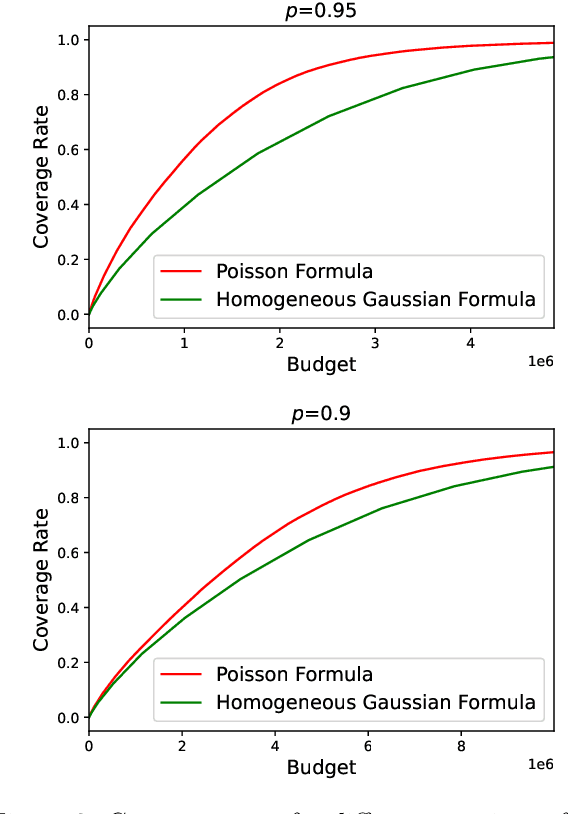
Abstract:The problem of low-rank matrix completion with heterogeneous and sub-exponential (as opposed to homogeneous and Gaussian) noise is particularly relevant to a number of applications in modern commerce. Examples include panel sales data and data collected from web-commerce systems such as recommendation engines. An important unresolved question for this problem is characterizing the distribution of estimated matrix entries under common low-rank estimators. Such a characterization is essential to any application that requires quantification of uncertainty in these estimates and has heretofore only been available under the assumption of homogenous Gaussian noise. Here we characterize the distribution of estimated matrix entries when the observation noise is heterogeneous sub-exponential and provide, as an application, explicit formulas for this distribution when observed entries are Poisson or Binary distributed.
Learning Treatment Effects in Panels with General Intervention Patterns
Jun 05, 2021

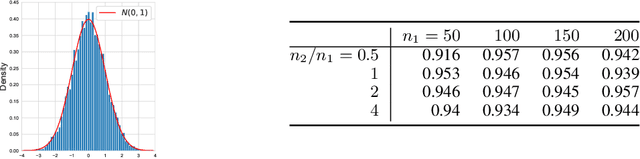
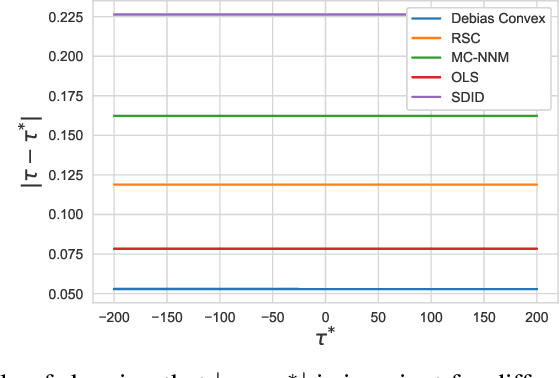
Abstract:The problem of causal inference with panel data is a central econometric question. The following is a fundamental version of this problem: Let $M^*$ be a low rank matrix and $E$ be a zero-mean noise matrix. For a `treatment' matrix $Z$ with entries in $\{0,1\}$ we observe the matrix $O$ with entries $O_{ij} := M^*_{ij} + E_{ij} + \mathcal{T}_{ij} Z_{ij}$ where $\mathcal{T}_{ij} $ are unknown, heterogenous treatment effects. The problem requires we estimate the average treatment effect $\tau^* := \sum_{ij} \mathcal{T}_{ij} Z_{ij} / \sum_{ij} Z_{ij}$. The synthetic control paradigm provides an approach to estimating $\tau^*$ when $Z$ places support on a single row. This paper extends that framework to allow rate-optimal recovery of $\tau^*$ for general $Z$, thus broadly expanding its applicability. Our guarantees are the first of their type in this general setting. Computational experiments on synthetic and real-world data show a substantial advantage over competing estimators.
Optimizing Offer Sets in Sub-Linear Time
Nov 17, 2020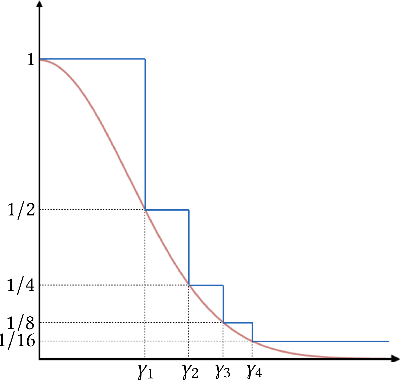
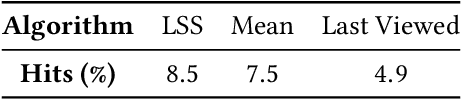

Abstract:Personalization and recommendations are now accepted as core competencies in just about every online setting, ranging from media platforms to e-commerce to social networks. While the challenge of estimating user preferences has garnered significant attention, the operational problem of using such preferences to construct personalized offer sets to users is still a challenge, particularly in modern settings where a massive number of items and a millisecond response time requirement mean that even enumerating all of the items is impossible. Faced with such settings, existing techniques are either (a) entirely heuristic with no principled justification, or (b) theoretically sound, but simply too slow to work. Thus motivated, we propose an algorithm for personalized offer set optimization that runs in time sub-linear in the number of items while enjoying a uniform performance guarantee. Our algorithm works for an extremely general class of problems and models of user choice that includes the mixed multinomial logit model as a special case. We achieve a sub-linear runtime by leveraging the dimensionality reduction from learning an accurate latent factor model, along with existing sub-linear time approximate near neighbor algorithms. Our algorithm can be entirely data-driven, relying on samples of the user, where a `sample' refers to the user interaction data typically collected by firms. We evaluate our approach on a massive content discovery dataset from Outbrain that includes millions of advertisements. Results show that our implementation indeed runs fast and with increased performance relative to existing fast heuristics.
Solving the Phantom Inventory Problem: Near-optimal Entry-wise Anomaly Detection
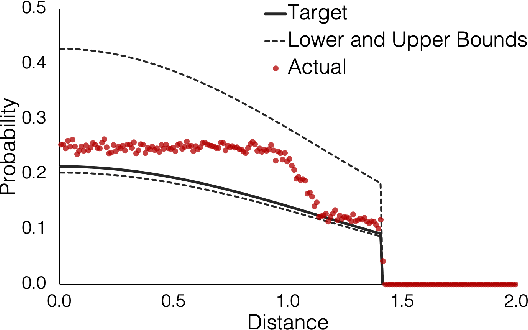
Jun 23, 2020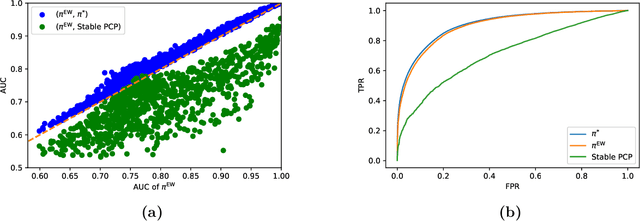
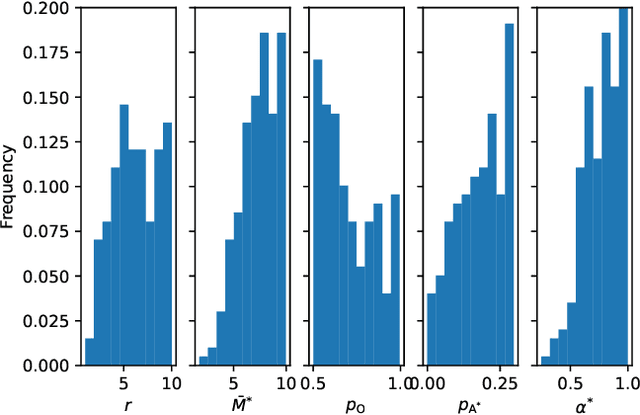
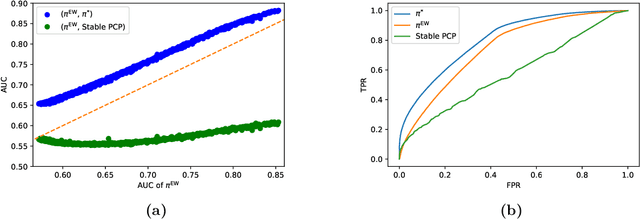
Abstract:We observe that a crucial inventory management problem ('phantom inventory'), that by some measures costs retailers approximately 4% in annual sales can be viewed as a problem of identifying anomalies in a (low-rank) Poisson matrix. State of the art approaches to anomaly detection in low-rank matrices apparently fall short. Specifically, from a theoretical perspective, recovery guarantees for these approaches require that non-anomalous entries be observed with vanishingly small noise (which is not the case in our problem, and indeed in many applications). So motivated, we propose a conceptually simple entry-wise approach to anomaly detection in low-rank Poisson matrices. Our approach accommodates a general class of probabilistic anomaly models. We extend recent work on entry-wise error guarantees for matrix completion, establishing such guarantees for sub-exponential matrices, where in addition to missing entries, a fraction of entries are corrupted by (an also unknown) anomaly model. We show that for any given budget on the false positive rate (FPR), our approach achieves a true positive rate (TPR) that approaches the TPR of an (unachievable) optimal algorithm at a min-max optimal rate. Using data from a massive consumer goods retailer, we show that our approach provides significant improvements over incumbent approaches to anomaly detection.
Causal Inference With Selectively-Deconfounded Data
Feb 25, 2020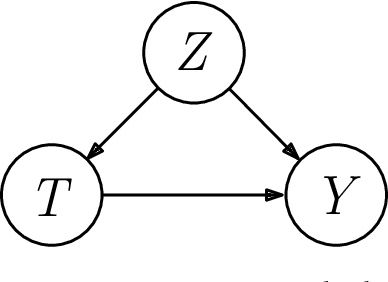
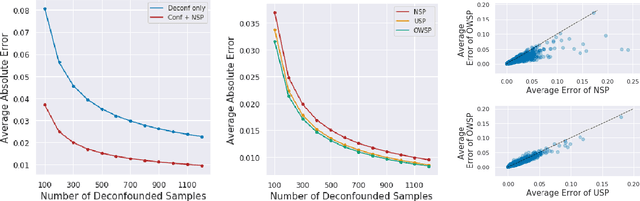
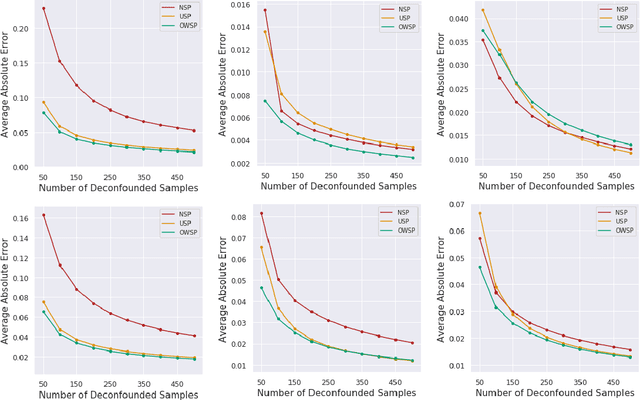
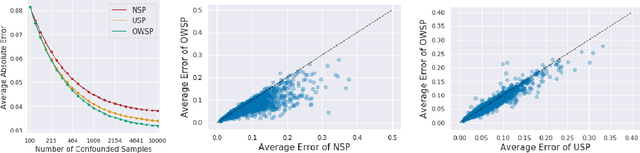
Abstract:Given only data generated by a standard confounding graph with unobserved confounder, the Average Treatment Effect (ATE) is not identifiable. To estimate the ATE, a practitioner must then either (a) collect deconfounded data; (b) run a clinical trial; or (c) elucidate further properties of the causal graph that might render the ATE identifiable. In this paper, we consider the benefit of incorporating a (large) confounded observational dataset alongside a (small) deconfounded observational dataset when estimating the ATE. Our theoretical results show that the inclusion of confounded data can significantly reduce the quantity of deconfounded data required to estimate the ATE to within a desired accuracy level. Moreover, in some cases---say, genetics---we could imagine retrospectively selecting samples to deconfound. We demonstrate that by strategically selecting these examples based upon the (already observed) treatment and outcome, we can reduce our data dependence further. Our theoretical and empirical results establish that the worst-case relative performance of our approach (vs. a natural benchmark) is bounded while our best-case gains are unbounded. Next, we demonstrate the benefits of selective deconfounding using a large real-world dataset related to genetic mutation in cancer. Finally, we introduce an online version of the problem, proposing two adaptive heuristics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge