Soft-Dropout: A Practical Approach for Mitigating Overfitting in Quantum Convolutional Neural Networks

Quantum convolutional neural network (QCNN), an early application for quantum computers in the NISQ era, has been consistently proven successful as a machine learning (ML) algorithm for several tasks with significant accuracy. Derived from its classical counterpart, QCNN is prone to overfitting. Overfitting is a typical shortcoming of ML models that are trained too closely to the availed training dataset and perform relatively poorly on unseen datasets for a similar problem. In this work we study the adaptation of one of the most successful overfitting mitigation method, knows as the (post-training) dropout method, to the quantum setting. We find that a straightforward implementation of this method in the quantum setting leads to a significant and undesirable consequence: a substantial decrease in success probability of the QCNN. We argue that this effect exposes the crucial role of entanglement in QCNNs and the vulnerability of QCNNs to entanglement loss. To handle overfitting, we proposed a softer version of the dropout method. We find that the proposed method allows us to handle successfully overfitting in the test cases.

Fast quantum state reconstruction via accelerated non-convex programming

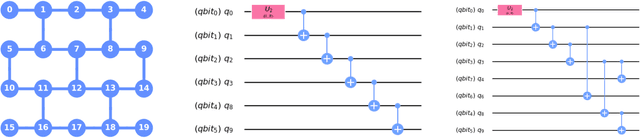
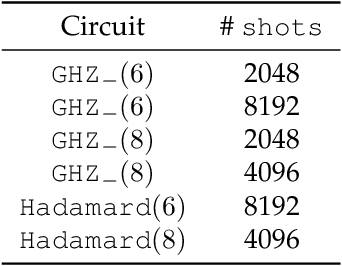
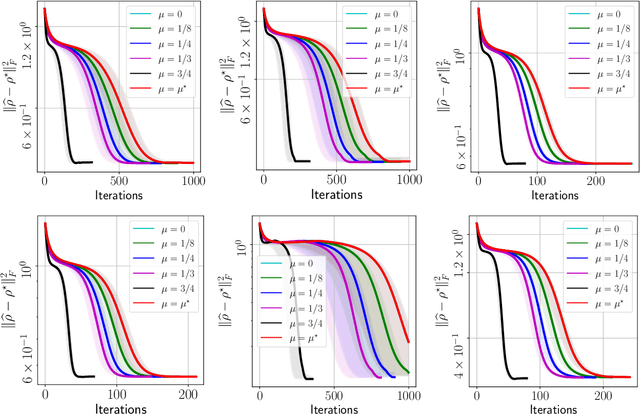
We propose a new quantum state reconstruction method that combines ideas from compressed sensing, non-convex optimization, and acceleration methods. The algorithm, called Momentum-Inspired Factored Gradient Descent (\texttt{MiFGD}), extends the applicability of quantum tomography for larger systems. Despite being a non-convex method, \texttt{MiFGD} converges \emph{provably} to the true density matrix at a linear rate, in the absence of experimental and statistical noise, and under common assumptions. With this manuscript, we present the method, prove its convergence property and provide Frobenius norm bound guarantees with respect to the true density matrix. From a practical point of view, we benchmark the algorithm performance with respect to other existing methods, in both synthetic and real experiments performed on an IBM's quantum processing unit. We find that the proposed algorithm performs orders of magnitude faster than state of the art approaches, with the same or better accuracy. In both synthetic and real experiments, we observed accurate and robust reconstruction, despite experimental and statistical noise in the tomographic data. Finally, we provide a ready-to-use code for state tomography of multi-qubit systems.

Estimating expectation values using approximate quantum states

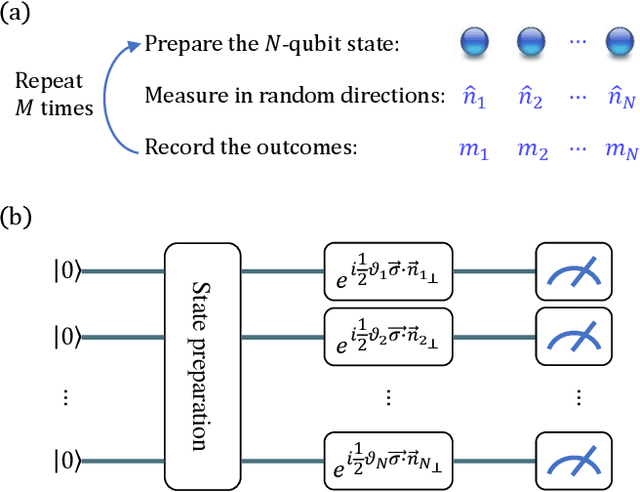
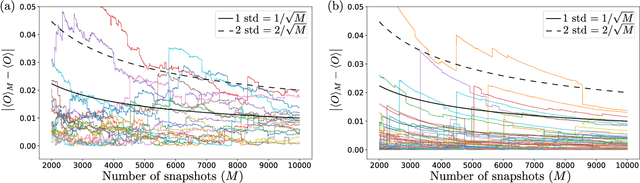
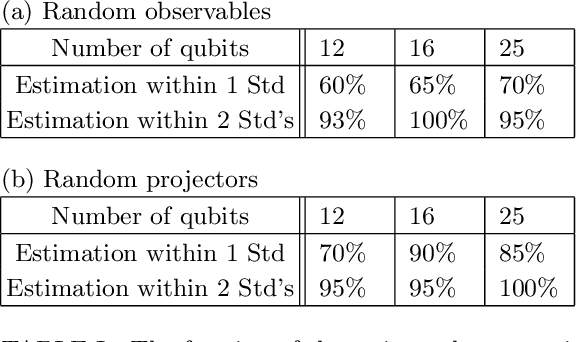
We introduce an approximate description of an $N$-qubit state, which contains sufficient information to estimate the expectation value of any observable to a precision that is upper bounded by the ratio of a suitably-defined seminorm of the observable to the square root of the number of the system's identical preparations $M$, with no explicit dependence on $N$. We describe an operational procedure for constructing the approximate description of the state that requires, besides the quantum state preparation, only single-qubit rotations followed by single-qubit measurements. We show that following this procedure, the cardinality of the resulting description of the state grows as $3MN$. We test the proposed method on Rigetti's quantum processor unit with 12, 16 and 25 qubits for random states and random observables, and find an excellent agreement with the theory, despite experimental errors.

Implicit regularization and solution uniqueness in over-parameterized matrix sensing

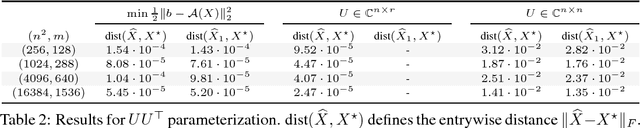
We consider whether algorithmic choices in over-parameterized linear matrix factorization introduce implicit regularization. We focus on noiseless matrix sensing over rank-$r$ positive semi-definite (PSD) matrices in $\mathbb{R}^{n \times n}$, with a sensing mechanism that satisfies the restricted isometry property (RIP). The algorithm we study is that of \emph{factored gradient descent}, where we model the low-rankness and PSD constraints with the factorization $UU^\top$, where $U \in \mathbb{R}^{n \times r}$. Surprisingly, recent work argues that the choice of $r \leq n$ is not pivotal: even setting $U \in \mathbb{R}^{n \times n}$ is sufficient for factored gradient descent to find the rank-$r$ solution, which suggests that operating over the factors leads to an implicit regularization. In this note, we provide a different perspective. We show that, in the noiseless case, under certain conditions, the PSD constraint by itself is sufficient to lead to a unique rank-$r$ matrix recovery, without implicit or explicit low-rank regularization. \emph{I.e.}, under assumptions, the set of PSD matrices, that are consistent with the observed data, is a singleton, irrespective of the algorithm used.