Emergence of Globally Attracting Fixed Points in Deep Neural Networks With Nonlinear Activations

Understanding how neural networks transform input data across layers is fundamental to unraveling their learning and generalization capabilities. Although prior work has used insights from kernel methods to study neural networks, a global analysis of how the similarity between hidden representations evolves across layers remains underexplored. In this paper, we introduce a theoretical framework for the evolution of the kernel sequence, which measures the similarity between the hidden representation for two different inputs. Operating under the mean-field regime, we show that the kernel sequence evolves deterministically via a kernel map, which only depends on the activation function. By expanding activation using Hermite polynomials and using their algebraic properties, we derive an explicit form for kernel map and fully characterize its fixed points. Our analysis reveals that for nonlinear activations, the kernel sequence converges globally to a unique fixed point, which can correspond to orthogonal or similar representations depending on the activation and network architecture. We further extend our results to networks with residual connections and normalization layers, demonstrating similar convergence behaviors. This work provides new insights into the implicit biases of deep neural networks and how architectural choices influence the evolution of representations across layers.

Learning Genomic Sequence Representations using Graph Neural Networks over De Bruijn Graphs

The rapid expansion of genomic sequence data calls for new methods to achieve robust sequence representations. Existing techniques often neglect intricate structural details, emphasizing mainly contextual information. To address this, we developed k-mer embeddings that merge contextual and structural string information by enhancing De Bruijn graphs with structural similarity connections. Subsequently, we crafted a self-supervised method based on Contrastive Learning that employs a heterogeneous Graph Convolutional Network encoder and constructs positive pairs based on node similarities. Our embeddings consistently outperform prior techniques for Edit Distance Approximation and Closest String Retrieval tasks.

Towards Training Without Depth Limits: Batch Normalization Without Gradient Explosion

Normalization layers are one of the key building blocks for deep neural networks. Several theoretical studies have shown that batch normalization improves the signal propagation, by avoiding the representations from becoming collinear across the layers. However, results on mean-field theory of batch normalization also conclude that this benefit comes at the expense of exploding gradients in depth. Motivated by these two aspects of batch normalization, in this study we pose the following question: "Can a batch-normalized network keep the optimal signal propagation properties, but avoid exploding gradients?" We answer this question in the affirmative by giving a particular construction of an Multi-Layer Perceptron (MLP) with linear activations and batch-normalization that provably has bounded gradients at any depth. Based on Weingarten calculus, we develop a rigorous and non-asymptotic theory for this constructed MLP that gives a precise characterization of forward signal propagation, while proving that gradients remain bounded for linearly independent input samples, which holds in most practical settings. Inspired by our theory, we also design an activation shaping scheme that empirically achieves the same properties for certain non-linear activations.

On the impact of activation and normalization in obtaining isometric embeddings at initialization

In this paper, we explore the structure of the penultimate Gram matrix in deep neural networks, which contains the pairwise inner products of outputs corresponding to a batch of inputs. In several architectures it has been observed that this Gram matrix becomes degenerate with depth at initialization, which dramatically slows training. Normalization layers, such as batch or layer normalization, play a pivotal role in preventing the rank collapse issue. Despite promising advances, the existing theoretical results (i) do not extend to layer normalization, which is widely used in transformers, (ii) can not characterize the bias of normalization quantitatively at finite depth. To bridge this gap, we provide a proof that layer normalization, in conjunction with activation layers, biases the Gram matrix of a multilayer perceptron towards isometry at an exponential rate with depth at initialization. We quantify this rate using the Hermite expansion of the activation function, highlighting the importance of higher order ($\ge 2$) Hermite coefficients in the bias towards isometry.

Entropy Maximization with Depth: A Variational Principle for Random Neural Networks

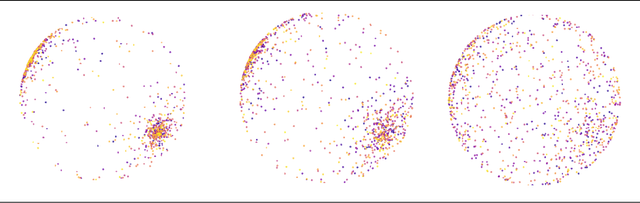
To understand the essential role of depth in neural networks, we investigate a variational principle for depth: Does increasing depth perform an implicit optimization for the representations in neural networks? We prove that random neural networks equipped with batch normalization maximize the differential entropy of representations with depth up to constant factors, assuming that the representations are contractive. Thus, representations inherently obey the \textit{principle of maximum entropy} at initialization, in the absence of information about the learning task. Our variational formulation for neural representations characterizes the interplay between representation entropy and architectural components, including depth, width, and non-linear activations, thereby potentially inspiring the design of neural architectures.

Batch Normalization Orthogonalizes Representations in Deep Random Networks

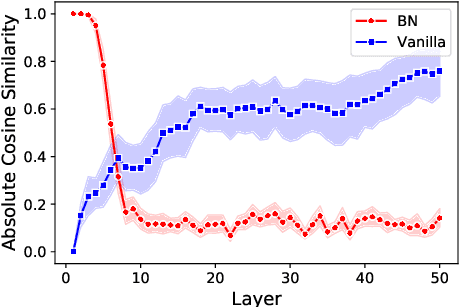
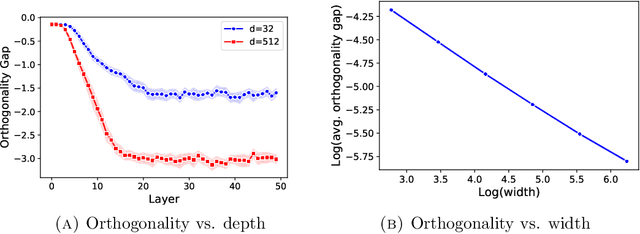
This paper underlines a subtle property of batch-normalization (BN): Successive batch normalizations with random linear transformations make hidden representations increasingly orthogonal across layers of a deep neural network. We establish a non-asymptotic characterization of the interplay between depth, width, and the orthogonality of deep representations. More precisely, under a mild assumption, we prove that the deviation of the representations from orthogonality rapidly decays with depth up to a term inversely proportional to the network width. This result has two main implications: 1) Theoretically, as the depth grows, the distribution of the representation -- after the linear layers -- contracts to a Wasserstein-2 ball around an isotropic Gaussian distribution. Furthermore, the radius of this Wasserstein ball shrinks with the width of the network. 2) In practice, the orthogonality of the representations directly influences the performance of stochastic gradient descent (SGD). When representations are initially aligned, we observe SGD wastes many iterations to orthogonalize representations before the classification. Nevertheless, we experimentally show that starting optimization from orthogonal representations is sufficient to accelerate SGD, with no need for BN.